If a vector →A is parallel to another vector →B then the resultant of the vector →A×→B will be equal to
A
→A
Zero vector
Zero
The correct Answer is:C
→A×→B=ABsinθˆn
for parallel vector θ=0∘or180∘,sinθ=0
∴Vec(A)×→B=ˆ0
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Problems Based On Mixed Concepts32videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Assertion Reasoning17videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Dot Product22videos
VECTORS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test28videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
Similar Questions
Three vectors →A,→B and →C are related as →A+→B=→C .If vector →C is perpendicular to vector →A and the magnitude of →C is equal to the magnitude of →A, what will be the angle between vectors →A and →B.
View SolutionThe vector →b=3j+4k is to be written as the sum of a vector →b1, parallel to →a=i+j, and a vector →b2, perpendicular to →a, then →b1, equals
View Solution
Knowledge Check
- Question 1 - Select One
Two vectors →Aand→B lie in plane, another vector →C lies outside this plane, then the resultant of these three vectors i.e., →A+→B+→C
ACan be zeroBcannnot be zeroCLies in the plane containing →A+→BDLies in the plane containing →C - Question 2 - Select One
If the vectors →kand→A are parallel to each other, what is k→k×→A equal to ?
Ak2→AB→0C−k2→AD→A - Question 3 - Select One
Two vector →A and →B have equal magnitudes. Then the vector →A+→B is perpendicular :
A→A×→BB→A−→BC3→A−3→BDAll of these
If →aand→b are two unit vectors, then the vector (→a+→b)×(→a×→b) is parallel to
View SolutionA vector →A is along the positive x- axis . If B is another vector such that →A×→B is zero , then B could be
View SolutionA vector →A is along the positive x-axis and its vector product with another vector →B is zero, then vector →B could be
View SolutionThe resultant of two vectors →A and →B is perpendicular to the vector →A and its magnitudes is equal to half of the magnitudes of vector →B (figure). The angle between →A and →B is
 View Solution
View SolutionKeeping one vector constant, if direction of other to be added in the first vector is changed continuously, tip of the resultant vector describes a circles, In the following figure vector →a is kept constant. When vector →b addede to →a changes its direction, the tip of the resultant vector →r=→a+→b describes circles of radius b with its centre at the tip of vector →a. Maximum angle between vector →a and the resultant →r=→a+→b is
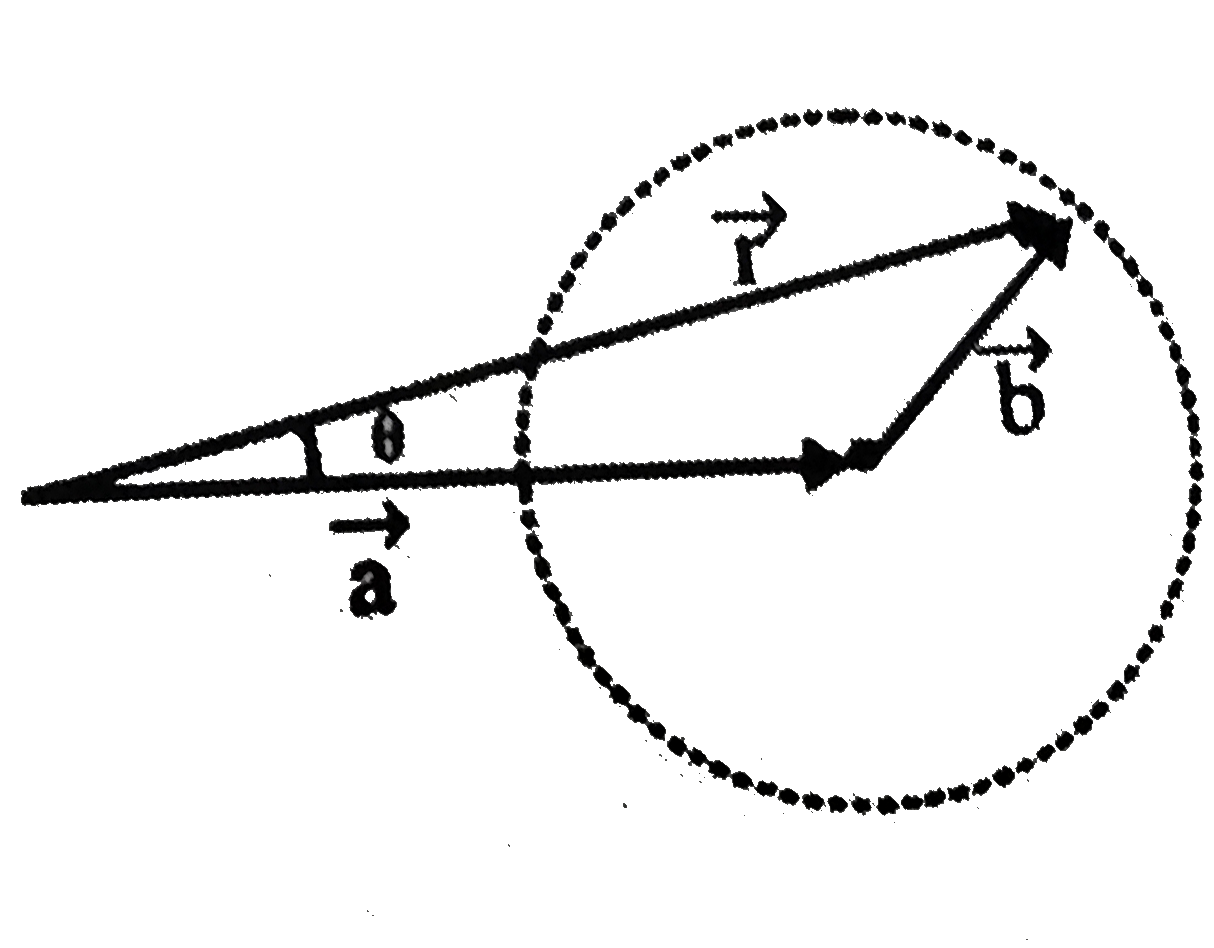 View Solution
View Solution

