A particle whose speed is 50ms−1 moves along the line from A(2,1) to B(9,25). Find its velocity vector in the from of aˆi+bˆj.
(7ˆi+24ˆj)m/s
2(7ˆi+24ˆj)m/s
4(7ˆi+24ˆj)m/s
5(7ˆi+24ˆj)m/s
The correct Answer is:B
→V=50(ˆAB)
−−→AB=(9−2)ˆi+(25−1)ˆj=(7ˆi+24ˆj)
∣∣∣−−→AB∣∣∣=√(72)+(24)2
ˆAB=7ˆi+24ˆj√(72)+(242)=(7ˆi+24ˆj)25
→V=50.(7ˆi+24ˆj)25=2(7ˆi+24ˆj)m/s
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Assertion Reasoning17videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - NEET Questions12videos
VECTORS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Cross Product25videos
VECTORS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test28videos
UNIT, DIMENSION AND ERROR ANALYSIS
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
Similar Questions
Knowledge Check
- Question 1 - Select One
A particle is moving with speed 6m/s along the direction of →A=2ˆi+2ˆj−ˆk, then its velocity is :
A(4ˆi+2ˆj−4ˆk) unitsB(4ˆi+4ˆj−2ˆk) unitsC(4ˆi+4ˆj−4ˆk) unitsD(2ˆi+4ˆj−2ˆk) units - Question 2 - Select One
A particle is moving with speed 6m/s along the direction of →A=2ˆi+2ˆj−ˆk, then its velocity is :
A(4ˆi+2ˆj)unitsB(4ˆi+4ˆj−2ˆk) unitsC(4ˆi+4ˆj−4ˆk) unitsD(2ˆi+4ˆj−2ˆk) units - Question 3 - Select One
If a particle moves from the point A(1,2,3) to the point B(4,6,9), its displacement vector be
Aˆi+ˆj+ˆkB2ˆi+3ˆj+4ˆkC3ˆi+4ˆj+6ˆkD3ˆi+4ˆj+5ˆk
A particle moves with a constant acceleration a=2ms−2 along a straight line. If it moves with an initial velocity of 5ms−1, then obtain an expression for its instantaneous velocity.
View SolutionA particle moves along the sides AB,BC,CD of a square of side 25m with a velocity of "15ms^(-1).Its average velocity is
View SolutionA particle moves in a straight line from A to B with speed v1 and then from B to A with speed v2. Find the average velocity and average speed.
View SolutionA particle moves along the side AB, BC, CD of a square of side 25 m with a velocity of 15ms−1Its average velocity is
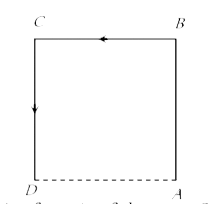 View Solution
View SolutionA particle is moving at uniform speed 2ms−1 along a circle of radius 0.5m.The centripetal acceleration of particle is
View Solution

