A ball is thrown from the top of tower with an initial velocity of at an angle of with the horizontal. If it hits the ground of a distance of 17.3m from the back of the tower, the height of the tower is
The correct Answer is:D
To solve the problem, we will follow these steps:
Step 1: Break down the initial velocity into components
The initial velocity u=10m/s is thrown at an angle of 30∘ with the horizontal. We can find the horizontal and vertical components of the velocity using trigonometric functions:
- Horizontal component ux=ucosθ=10cos30∘=10×√32=5√3m/s
- Vertical component uy=usinθ=10sin30∘=10×12=5m/s
Step 2: Calculate the time of flight
The horizontal distance covered by the ball is given as 17.3m. We can use the horizontal motion to find the time of flight t:
Distance=Velocity×Time⟹t=Distanceux=17.35√3
Calculating t:
t=17.35×1.732≈17.38.66≈2s
Step 3: Use the vertical motion to find the height of the tower
Now we can use the vertical motion to find the height h of the tower. The vertical displacement can be calculated using the second equation of motion:
h=uyt−12gt2
Substituting the known values:
- uy=5m/s
- g=10m/s2
- t=2s
Calculating h:
h=5×2−12×10×(2)2
h=10−12×10×4
h=10−20=−10m
Since height cannot be negative, we interpret this as the height of the tower being 10m above the ground.
Final Answer
The height of the tower is 10m.
---
The initial velocity u=10m/s is thrown at an angle of 30∘ with the horizontal. We can find the horizontal and vertical components of the velocity using trigonometric functions:
- Vertical component uy=usinθ=10sin30∘=10×12=5m/s
The horizontal distance covered by the ball is given as 17.3m. We can use the horizontal motion to find the time of flight t:
Now we can use the vertical motion to find the height h of the tower. The vertical displacement can be calculated using the second equation of motion:
- g=10m/s2
- t=2s
h=10−12×10×4
h=10−20=−10m
The height of the tower is 10m.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projection From Inclined Plane20videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Relative Velocity In Two Dimensions23videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test29videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
Similar Questions
A ball is thrown from the top of a tower with an initial velocity of 10 m//s at an angle of 30∘above the horizontal. It hits the ground at a distance of 17.3 m from the base of the tower. The height of the tower (g=10m/s2) will be
View SolutionA ball is thrown from the top of a tower with an intial velocity of 10 m//s at an angle 37∘ above the horizontal, hits the ground at a distance 16 m from the base of tower. Calculate height of tower. [g=10m/s2]
View Solution
Knowledge Check
- Question 1 - Select One
An object is thrown towards the tower which is at a horizontal distance of 50 m with an initial velocity of 10ms−1 and making an angle 30∘ with the horizontal. The object hits the tower at certain height. The height from the bottom of the tower, where the object hits the tower is (Take, g=10ms−2)
A50√3[1−10√3]mB503[1−10√3]mC100√3[1−10√3]mD1003[1−10√3]m - Question 2 - Select One
A stone is thrown from the top of a tower of height 50m with a velocity of 30ms−1 at an angle of 30∘ above the horizontal.Find the time during which the stone will be in air
A2secB3secC4secD5sec - Question 3 - Select One
A ball is projected upwards from the top of a tower with a velocity 50ms−1 making an angle 30∘ with the horizontal. The height of tower is 70m. After how many seconds from the instant of throwing, will the ball reach the ground. (g=10ms−2)
A2 sB5 sC7 sD9 s
A ball is thrown from the top of a tower of 61m high with a velocity 24.4ms−1 at an elevation of 30∘ above the horizontal. What is the distance from the foot of the tower to the point where the ball hits the ground?
View SolutionA stone is thrown up from the top of a tower 20,m with a velocity of 24m/s a tan elevation of 30∘ above the horizontal. Find the horizontal distance from the foot of the tower to the point at which the stone hits the ground. Take g=10m/s2
View SolutionA ball is thrown from the top of a 35m high tower with initial velocity of magnitude u=80 ms−1 at an angle 25∘ with horizontal.
Find the time to reach the ground and the horizontal distance covered by the ball.View SolutionA ball is thrown from the top of 36m high tower with velocity 5m/ss at an angle 37∘ above the horizontal as shown. Its horizontal distance on the ground is closest to [g=10m/s2
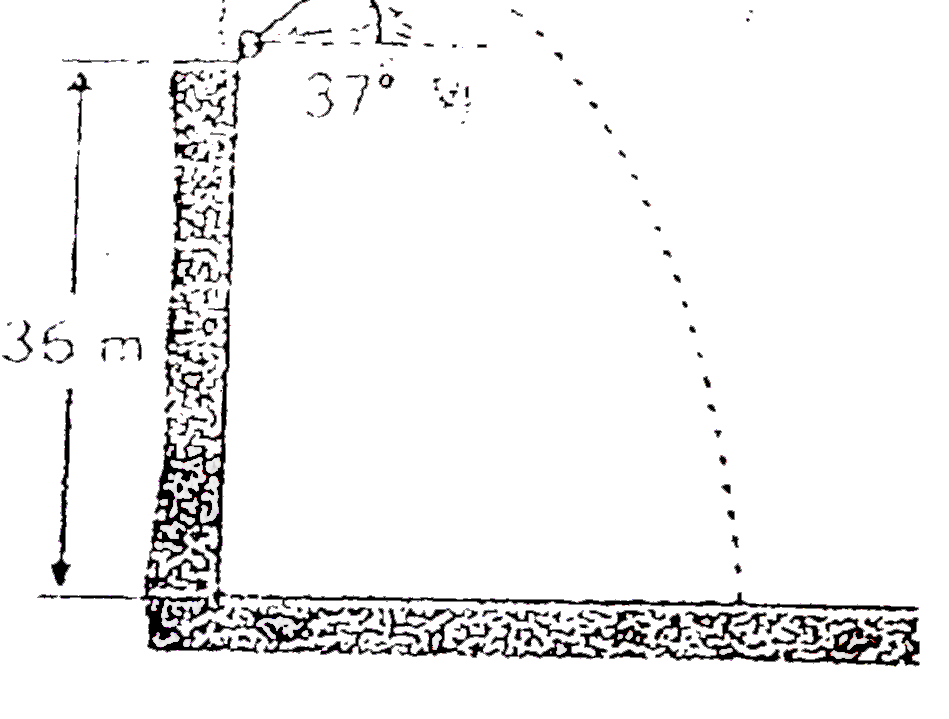 : View Solution
: View SolutionA stone is thrown from the top of a tower at an angle of 30∘ above the horizontal level with a velocity of 40 m/s. it strikes the ground after 5 second from the time of projection then the height of the tower is
View Solution

