A particle is projected with velocity 30∘ above on an inclined plane, inclination of which from horizontal is 37∘. Choose the appropriate path (air resistance is negligible)



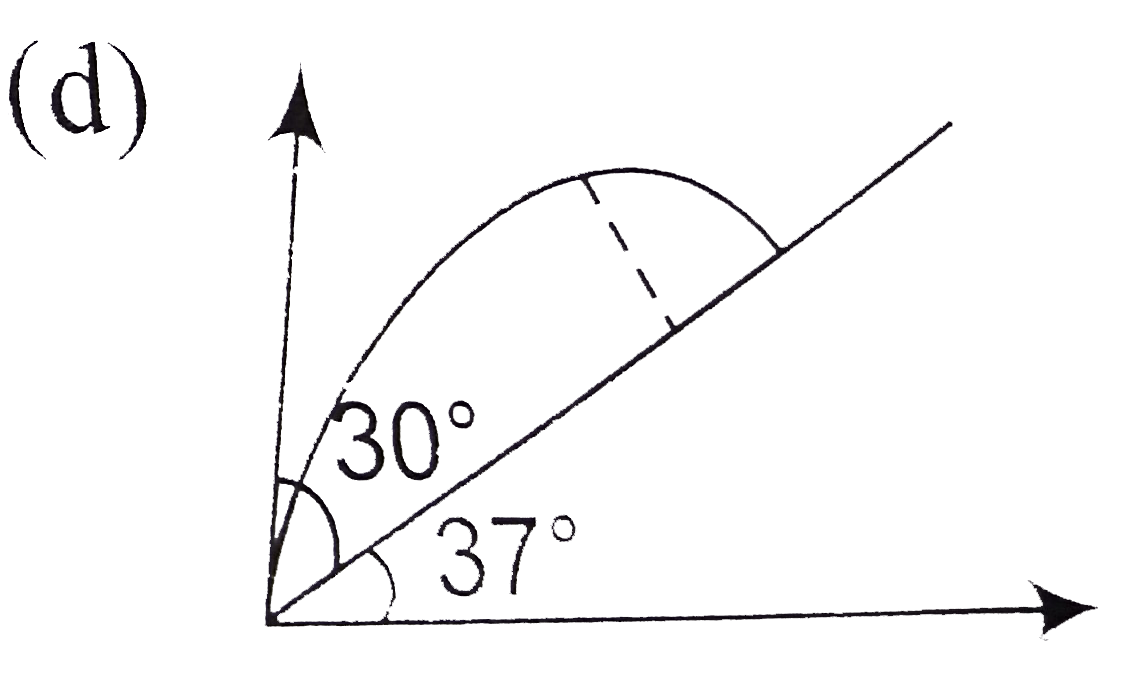
The correct Answer is:D
β>α
Topper's Solved these Questions
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Relative Velocity In Two Dimensions
23 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Kinematics Of Circular Motion
26 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projectile From A Height And Movingframe
19 Videos
- MOCK TESTBOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration
15 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
Similar Questions
A particle is projected from the bottom of an inclined plane of inclination 30∘. At what angle α(from the horizontal) should the particle be projected to get the maximum range on the inclined plane.
View SolutionAn particle is projected with velocity u on an inclined plane at an angle θ with the plane. If the particle lands on the plane at right Angle and its time of flight is ucosecθ2g. Find the angle of inclination of the plane with horizontal.
View Solution
Knowledge Check
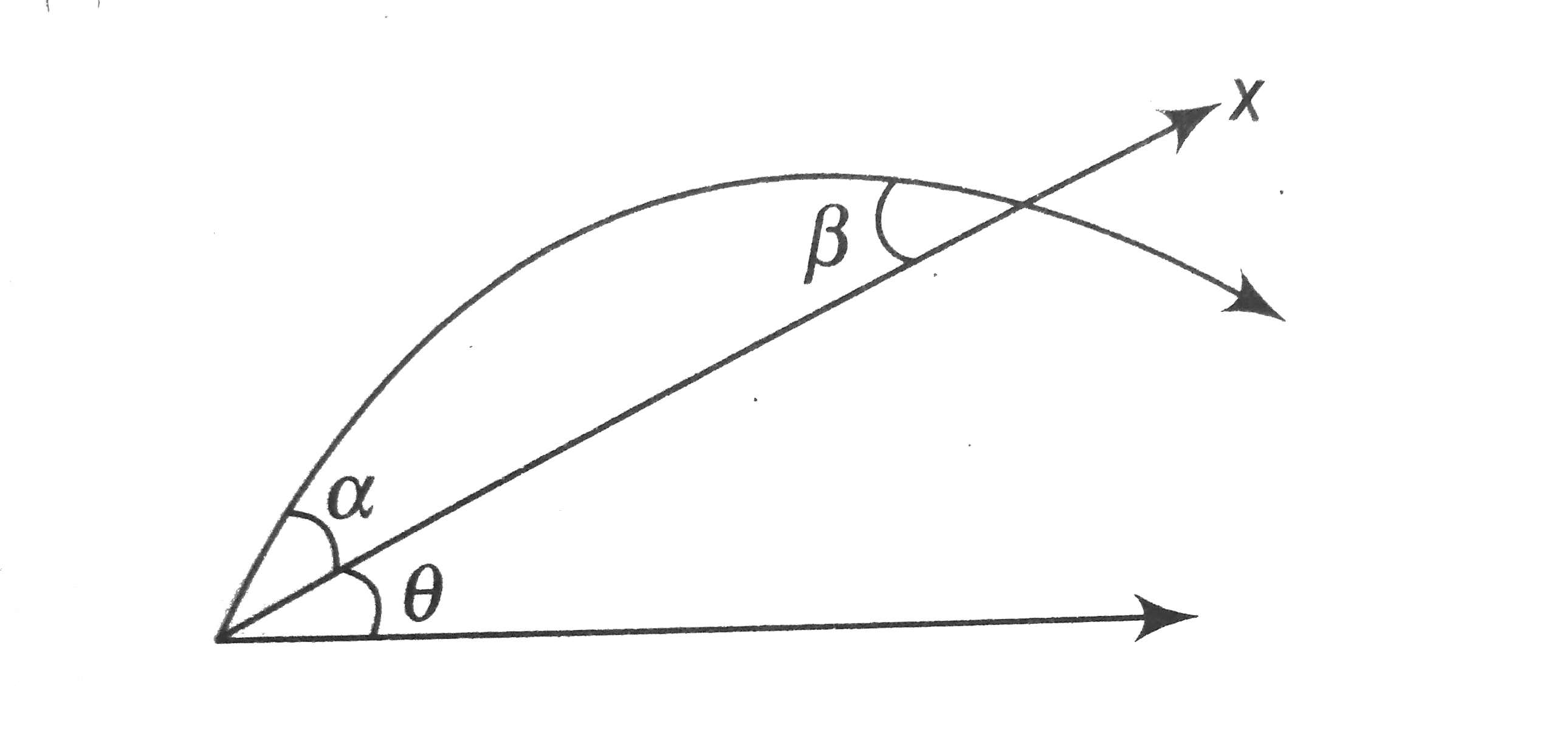
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
Atan(α−β)=cotβB2tan(α−β)=cotβC2cot(α−β)=cotβDNone of theseA particle is projected with a velocity of 20 m/s at an angle of 30∘ to an inclined plane of inclination 30∘ to the horizontal. The particle hits the inclined plane at an angle 30∘, during its journey. The time of flight is -
A4√3B2√3C√3D√32A particle is projected wityh velocity 20 ms−1 at angle 60∘ above horizontal up on an inclined plane having inclination 30∘. Find its shortest distance from the inclined plane when it is moving 53∘ above horizontal.
(Using =10ms−2)A11.1mB8.2mC3.3mD14.4m
A particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is fired horizontally form an inclined plane of inclination 30∘ with horizontal with speed 50ms−1. If g=10ms−2 , the range measured along the incline is
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View SolutionA particle is projected with a certain velocity at an angle ∝ above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally, then ∝ is equal to.
View SolutionA particle is projected on a frictionless inclined plane of inclination 37∘ at an angle of projection 45∘ from the inclined plane as shown in the figure. If after the first collision from the plane, the particle returns to its point of projection, then what is the value of the reciprocal of the coefficient of restitution between the particle and the plane?
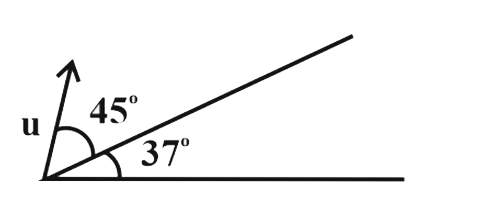
View Solution
