A man runs along a horizontal road holding his umrella vertical in order to afford maximum protection form rain. The rain is actually.
Falling vertical
Comming from front of the man
Coming from the back of the man
Either of (a), (b) or (c)
The correct Answer is:c
To solve the problem, we need to analyze the situation using vector components. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Problem
The man is running horizontally while holding his umbrella vertically. We need to determine the direction from which the rain appears to be falling relative to the man.
Step 2: Define the Velocities
Let:
- vm = velocity of the man (horizontal)
- vr = velocity of the rain (vertical)
Step 3: Set Up the Coordinate System
Assume the man is running to the right. We can define:
- The horizontal direction (to the right) as positive.
- The vertical direction (downward) as negative.
Step 4: Analyze the Rain's Velocity Relative to the Man
As the man runs, he perceives the rain to be falling at an angle. The velocity of the rain relative to the man can be expressed as:
vrm=vr−vm
Here, vrm is the velocity of the rain with respect to the man.
Step 5: Determine the Resultant Velocity
To find the resultant velocity of the rain as observed by the man, we need to consider both the horizontal and vertical components:
- The vertical component remains vr (downward).
- The horizontal component is −vm (to the left, since the man is running to the right).
Step 6: Calculate the Angle of the Resultant Velocity
The resultant velocity vector can be found using the Pythagorean theorem:
vresultant=√v2r+v2m
The angle θ at which the rain appears to fall can be calculated using:
tan(θ)=vrvm
Step 7: Conclusion
Since the man is running horizontally, the rain appears to be falling at an angle towards him from the back. Therefore, the rain appears to be coming from behind him.
Final Answer
The rain is actually falling vertically, but due to the man's horizontal motion, it appears to be coming from behind him.
---
The man is running horizontally while holding his umbrella vertically. We need to determine the direction from which the rain appears to be falling relative to the man.
Let:
- vm = velocity of the man (horizontal)
- vr = velocity of the rain (vertical)
Assume the man is running to the right. We can define:
- The horizontal direction (to the right) as positive.
- The vertical direction (downward) as negative.
As the man runs, he perceives the rain to be falling at an angle. The velocity of the rain relative to the man can be expressed as:
vrm=vr−vm
Here, vrm is the velocity of the rain with respect to the man.
To find the resultant velocity of the rain as observed by the man, we need to consider both the horizontal and vertical components:
- The vertical component remains vr (downward).
- The horizontal component is −vm (to the left, since the man is running to the right).
The resultant velocity vector can be found using the Pythagorean theorem:
vresultant=√v2r+v2m
The angle θ at which the rain appears to fall can be calculated using:
tan(θ)=vrvm
Since the man is running horizontally, the rain appears to be falling at an angle towards him from the back. Therefore, the rain appears to be coming from behind him.
The rain is actually falling vertically, but due to the man's horizontal motion, it appears to be coming from behind him.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Kinematics Of Circular Motion26videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Problems Based On Mixed Concepts35videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Projection From Inclined Plane20videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - MOCK TESTEXERCISE - Motion With Constant Acceleration15videos
MOCK TEST
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
Similar Questions
A boy is running on a horizontal road with a velocity of 5 m/s. At what angle should he hold his umbrella in order to protect him self from the rain if the rain is falling vertically with a velocity of 10 m/s?
View SolutionA man running on a horizontal road at 6km/h finds the rain falling vertically. He doubles his speed and find that the raindrops make an angle 37∘ with the vertical. Find the velocity of rain with respect to the ground.
View Solution
Knowledge Check
- Question 1 - Select One
A man walking downhill with velocity V0 finds that his umbrella gives him maximum protection from rain when he holds it such that the stick is perpendicular to the hill surface. When the man turns back and climbs the hill with velocity V0, he finds that it is most appropriate to hold the umbrella stick vertical. then the actual speed of raindrops in terms of V0 is : (the inclination of the hill is θ=37∘)
 A√63V03B√71V03C√73V03D√87V03
A√63V03B√71V03C√73V03D√87V03 - Question 2 - Select One
A person is standing on road by holding an umbrella at right angle to the horizontal surface in order to protect himself from rain falling at a speed of 10 m/s, when the velocity of wind is zero. Suddenly wind begins to flow at a speed of 20m/s, 30∘ south of west. Now by what angle the person has to rotate his umbrella in order to protect himself from rain ?
A30∘Btan−1(2)C60∘Dtan−1(√32) - Question 3 - Select One
Statement -1 : A man standing on the ground has to hold his umbrella at an angle θ with the vertical to protect himself from rain. It is possible that the man now starts running on the ground with certain speed, but he still has to hold his umbrella at angle θ with the vertical to protect himself from rain.
Statement -2 : Vertical component of velocity of rain w.r.t man does not change. if he starts running on a horizontal ground.AStatement -1 is Ture, statement -2 is Ture, Statement -2 is a correct explanation for statement -1 .BStatement -1 is True, statement -2 is True, statement - 2 is NOT a correct explanation for statement -3CStatement -1 is True, Statement -2 si FalseDStatement -1 is False ,Statement -2 is True.
A man is going in a topless car with a velocity of 10.8kmph."l It is raining vertically downwards.He has to hold the umbrella at angle 530 to the vertical to protect himself from rain.The actual velocity of the rain is (cos530=35)
View SolutionA man standing on a road has to hold his umbrella at 30∘ with the vertical to keep the rain away. He throws the umbrella and starts running at 10km/hr. He finds that rain drop are hitting his head vertically. Find the speed of rain drops with respect to (a) road (b) the moving man.
View SolutionA man running on the horizontal road at 8kmh−1 find the rain appears to be falling vertically. He incresases his speed to 12kmh−1 and find that the drops make angle 302 with the vertical. Fin dthe speed and direction of the rain with respedt to the road.
View SolutionA man running at a speed of 5 km/h finds that the rain is falling vertically. When the stops running, the finds that the rain is falling at an angle of 60∘ with the horizontal. The velocity of rain with respect to running man is
View SolutionA man is standing on incline which makes θ with horizontal and rain is falling vertically with respect to man. Now man starts walking along the incline. Mark the correct option
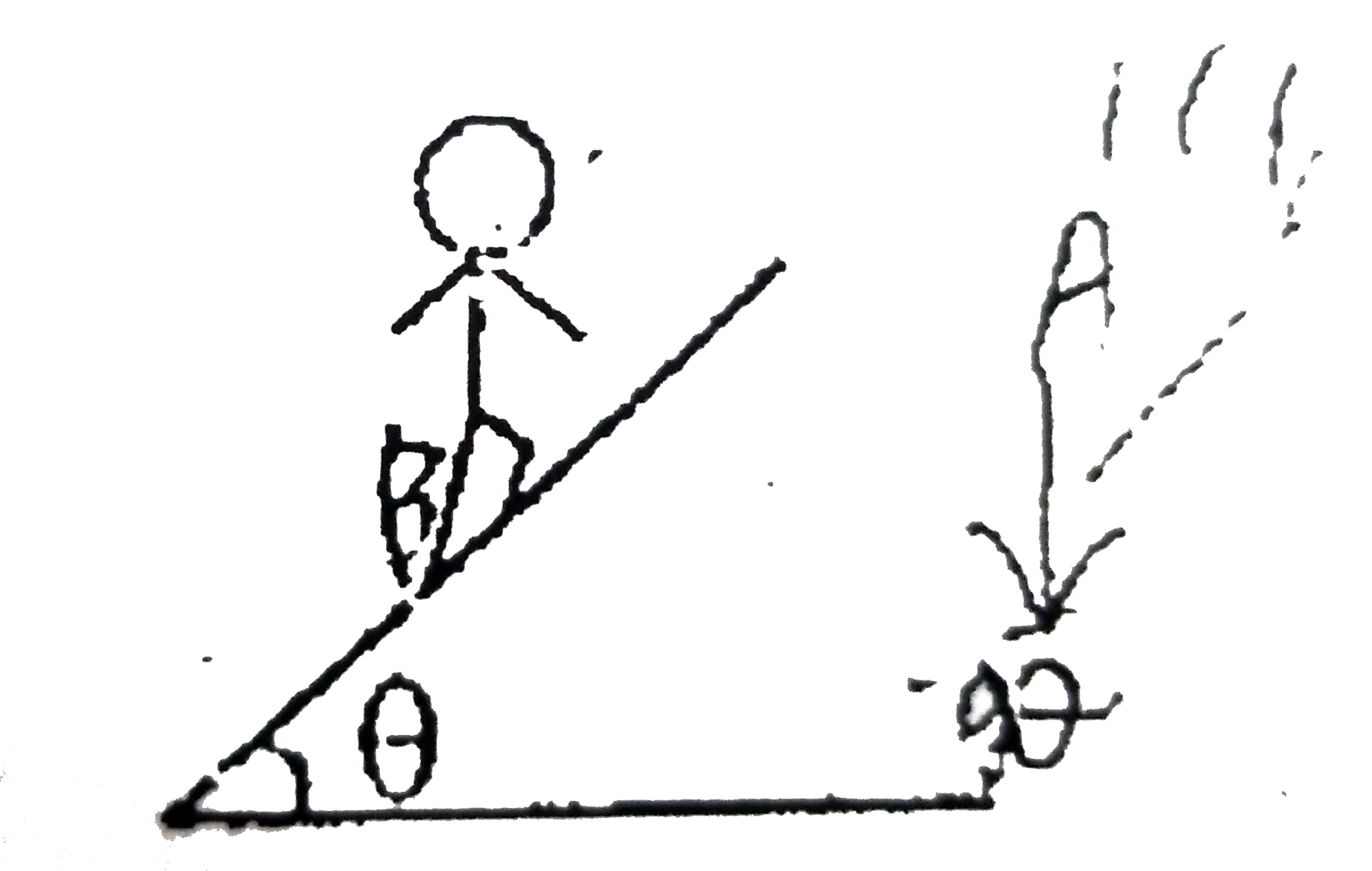 View Solution
View Solution

