A block of mass 3kg is placed on a rough horizontal surface (μs=0.4) . A force of 8.7N is applied on the block. The force of friction between the block and floor is .
8.7N
12N
10N
zero
The correct Answer is:A
To solve the problem, we need to determine the force of friction acting on the block when a force of 8.7 N is applied. Here’s a step-by-step solution:
Step 1: Calculate the weight of the block
The weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=3kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
Calculating the weight:
W=3kg×10m/s2=30N
Step 2: Determine the normal force (N)
On a horizontal surface, the normal force (N) is equal to the weight of the block:
N=W=30N
Step 3: Calculate the maximum static friction force
The maximum static friction force (f_s) can be calculated using the coefficient of static friction (μ_s):
fs=μs⋅N
where:
- μs=0.4
Calculating the maximum static friction:
fs=0.4×30N=12N
Step 4: Compare the applied force with the maximum static friction
The applied force (F) is given as:
F=8.7N
Now, we compare the applied force with the maximum static friction:
- Maximum static friction = 12 N
- Applied force = 8.7 N
Since 8.7N<12N, the block will not move.
Step 5: Determine the actual force of friction
Since the applied force is less than the maximum static friction, the actual force of friction (f) will be equal to the applied force:
f=F=8.7N
Conclusion
The force of friction between the block and the floor is 8.7 N.
---
The weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=3kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
W=3kg×10m/s2=30N
On a horizontal surface, the normal force (N) is equal to the weight of the block:
N=W=30N
The maximum static friction force (f_s) can be calculated using the coefficient of static friction (μ_s):
fs=μs⋅N
where:
- μs=0.4
fs=0.4×30N=12N
The applied force (F) is given as:
F=8.7N
- Maximum static friction = 12 N
- Applied force = 8.7 N
Since the applied force is less than the maximum static friction, the actual force of friction (f) will be equal to the applied force:
f=F=8.7N
The force of friction between the block and the floor is 8.7 N.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Dynamics Of Circular Motion31videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Problems Based On Mixed Concepts51videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Applications Of Newton'S Laws Of Motion33videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test29videos
MOTION IN TWO DIMENSION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
Similar Questions
A block of mass 2 kg is placed on the floor (μ=0.4). A horizontal force of 7 N is applied on the block. The force of friction between the block & floor is fs. Find the fs.
View SolutionA block of mass 1 kg in kept on a rough horizontal surface with μs=0.1 . A force of 0.5 N is applied as shown in the figure. What is the frictional force applied by ground on the block?
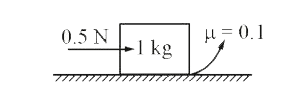 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 3kg is placed on a rough horizontal surface (μs=0.4) . A force of 8.7N is applied on the block. The force of friction between the block and floor is .
A8.7NB12NC10NDzero - Question 2 - Select One
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)
 A1.5 NB3 NC4 ND2.5 N
A1.5 NB3 NC4 ND2.5 N - Question 3 - Select One
A block of mass m is placed on a rough horizontal surface. If minimum force to pull the block is mg2 then coefficient of friction is :
A12B√3C1√3DNone
A block of mass 5kg is placed on a rough horizontal plane.A time dependent horizontal force F=(t2+2t) N acts on the block. The friction force between the block and the plane at t=3s is (μ=0.4)
View SolutionA block of mass m slips on a rough horizontal table under the action of horiozontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force aplied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table ?
 View Solution
View SolutionA block of mass 5kg is initially at rest on a rough horizontal surface. A force of 45N acts over a distance of 2m. The force of friction acting on the block is 25N. The final kinetic energy of the block is
View SolutionA block of mass 2 kg is placed on the floor . The coefficient of static friction is 0.4 . If a force of 2.8 N is applied on the block parallel to floor , the force of friction between the block and floor is : (Taking g = 10m/s2)
View SolutionA block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)
 View Solution
View Solution

