Two masses are connected by a string which passes over a pulley acceleration upward at a rate shown. If and be the accelerations of bodies 1 and 2 respectively then,
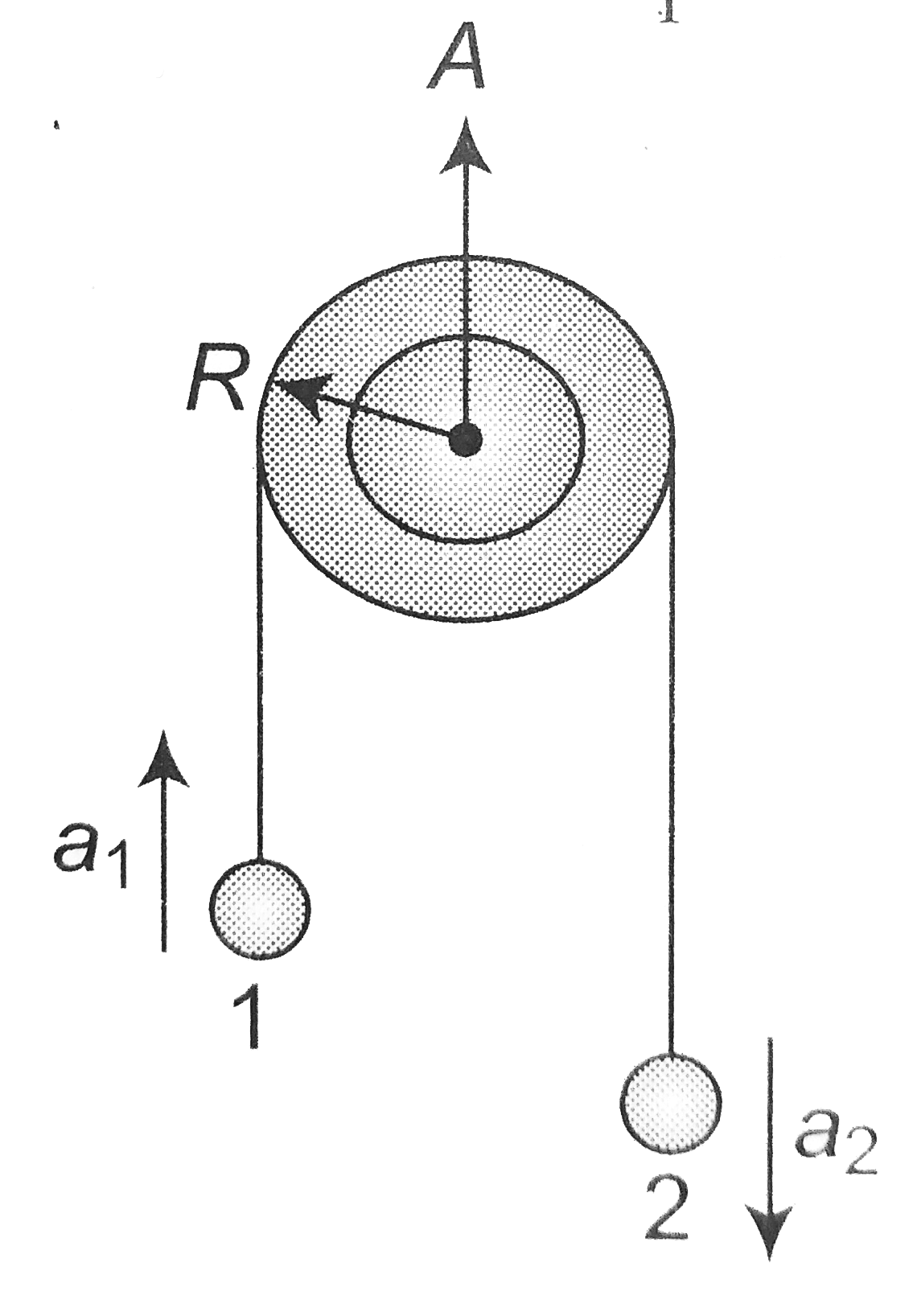
The correct Answer is:D
Since length of the string is constant So,
=constant.
Take derivative of both sides twice w.r.t. time ,
We get,
implies . 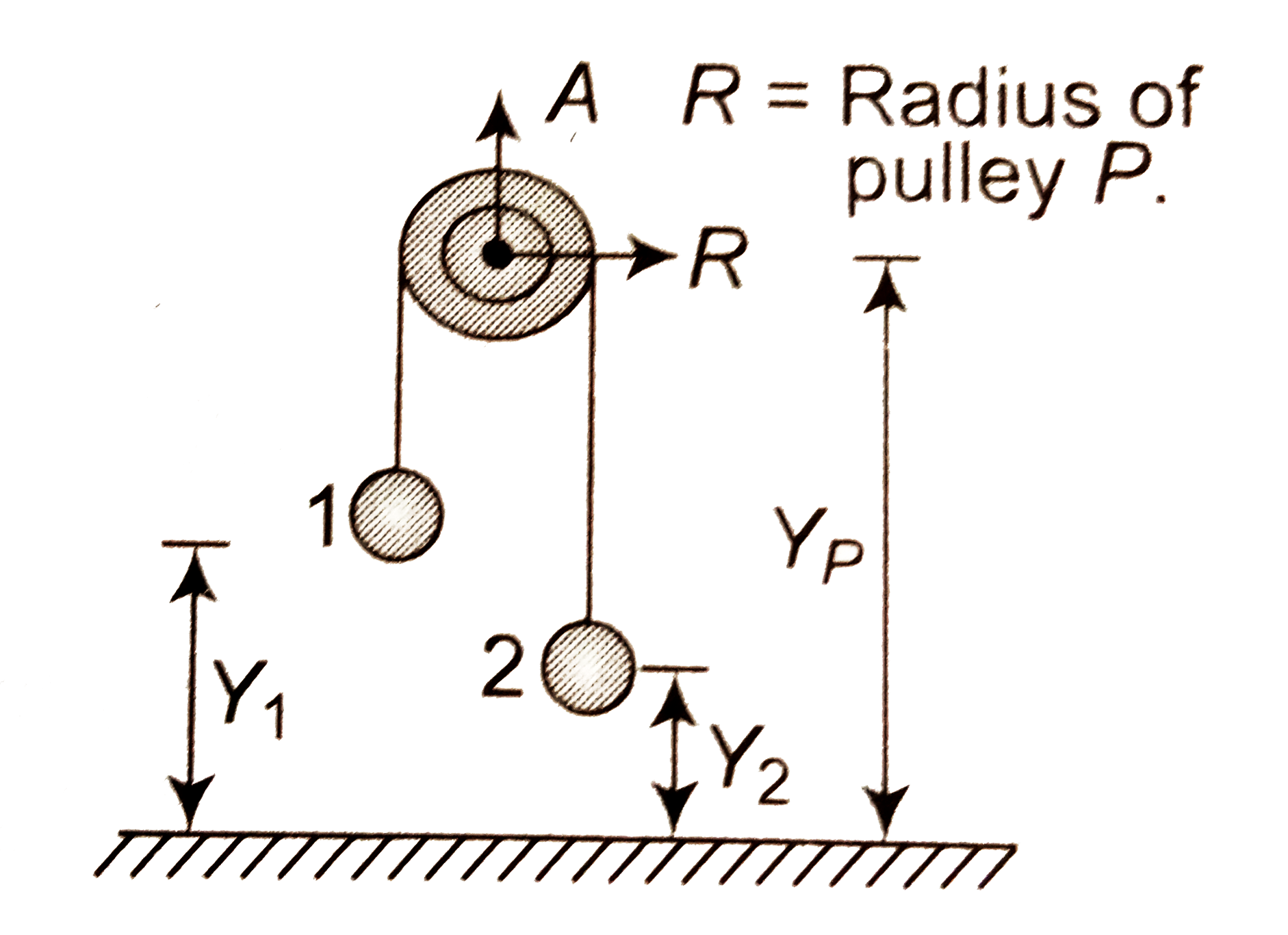
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - AIIMS Questions
26 Videos
- MOTION IN TWO DIMENSIONBOOK - A2ZCHAPTER - MOTION IN TWO DIMENSIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
Similar Questions
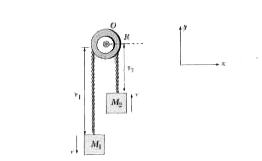
A block of mass M1 and a block of mass M2 are connected by a string that passes over a pulley as shown in Fig. The pulley is a uniform disk of radius R and mass M. Find the acceleration of the two object, using the concepts of angular momentum and torque.
View SolutionA block of mass m1 rests on a horizontal table. A string tied to the block is passed on a frictionless pulley fixed at the end of the table and to the other end of string is hung another block of mass m2. The acceleration of the system is
View Solution
Knowledge Check
If pulleys shown in the diagram are smooth and massless and a1 and a2 are acceleration of blocks of mass 4 kg and 8 kg respectively, then -
 Aa1=a2Ba1=2a2C2a1=2a2Da1=4a2
Aa1=a2Ba1=2a2C2a1=2a2Da1=4a2Two masses m1 and m2 are attached to a string which passes over a frictionless smooth pulley. When m1=10kg,m2=6kg, the acceleration of masses is
 A20m/s2B5m/s2C2.5m/s2D10m/s2
A20m/s2B5m/s2C2.5m/s2D10m/s2Two blocks of mass 2 kg and 5 kg are at rest on the ground. The masses are connected by a string passing over a frictionless pulley which is under the influence of a constant upward force F = 50N. The acceleration of 5 kg and 2 kg masses are
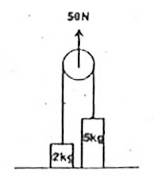 A0,2.5m/s2B0, 0C2.5m/s2,2.5m/s2D1m/s2,2.5m/s2
A0,2.5m/s2B0, 0C2.5m/s2,2.5m/s2D1m/s2,2.5m/s2
Two blocks are connected by an inextensible light string, the string is passing over smooth, light pulley as shown. Find the acceleration of blocks and tension in the string, reaction in pulley.

View SolutionIn the adjacent figure, all the pulleys are frictioniess and massless, all the stringes are also massless. The relation between a1,a2 and a3 is (where a1,a2 and a3 are the acceleration of masses m1,m2 and m3 respectively in the direction as shown in the figure)
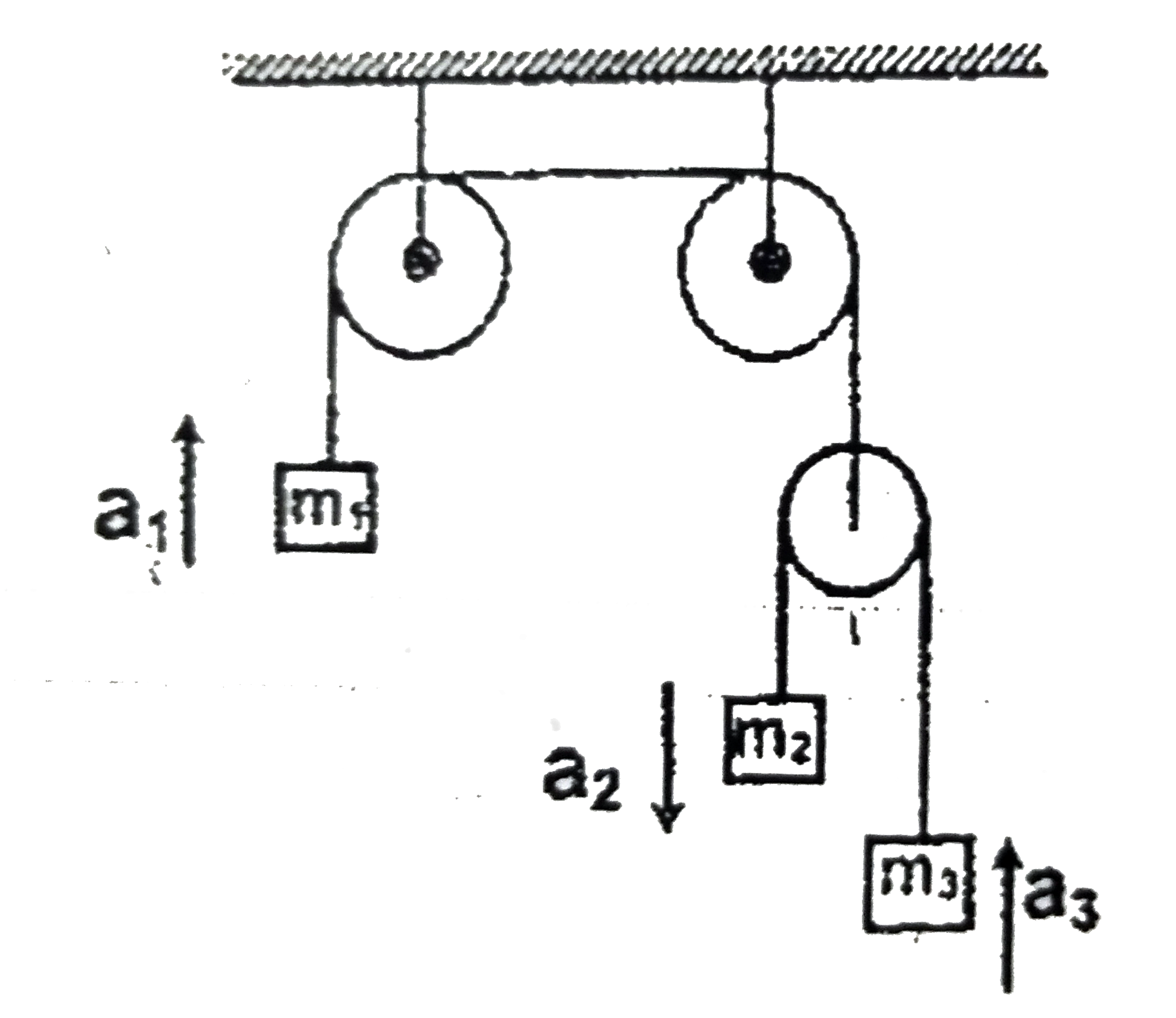
View SolutionTwo masses of 8kg and 4kg are connected by a string as shown in figure over a frictionless pulley.The acceleration of the system is

View SolutionTwo masses of 8 kg and 4 kg are connected by a string as shown in figure over a frictionless pulley. The acceleration of the system is

View SolutionTwo blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.

View Solution
