N identical balls are placed on a smooth horizontal surface. An another ball of same mass collides elastically with velocity u with first ball of N balls. A process of collision is thus started in which first ball collides with second ball and the with the third ball and so on. The coefficient of restitution for each collision is e. Find the speed of Nth ball.
(1+e)Nu
u(1+e)N−1
u(1+e)N−12N−1
uN(1+e)N
The correct Answer is:C
After collision, first ball start moving with velocity u
Now,e=V2−V1u
or V1=u−V2
so, e=V2−u+V2u
or V2=u(1+e)2
Incoming velocity of second ball is V2 and after collision velocity of third ball is V3 and velocity of second ball is V'2
e=V3−V'2V2
and mV2−mV3+3mV'2
or V'2=V2−V3
=u(1+e)2−V3=u(1+e)2−V3
So, e=V3−[u+ue−2V32][u(1+e)2]
On solving V3=u(1+e)222
so, velocity of Nth ball =u(1+e)N−12N−1
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Problems Based On Mixed Concepts
32 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Circular Motion In Vertical Plane
21 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
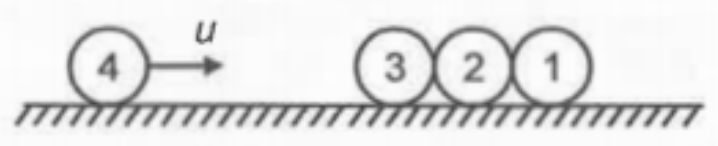
Three identical balls 1, 2 and 3 are placed together at rest on a smooth horizontal surface. A fourth identical ball moving with velocity u in line of first three balls collides head on elastically as shown in figure, then
View SolutionA glass ball collides with an identical ball at rest with v0=2 m/sec. If the coefficient of restitution of collision is e = 0.5, find the velocities of the glass balls just after the collision.
View Solution
Knowledge Check
A steel ball of radius 2cm is at rest on a frictionless surface. Another ball of radius 4cm moving at a velocity of 81cm/see collides elast cally with first ball. After collision the smaller ball moves with speed of
A81 cm/secB63 cm/secC144 cm/secDNone of theseA steel ball of radius 2cm is at rest on a frictionless surface. Another ball of radius 4cm moving at a velocity of 81cm/sec collides elastically with first ball. After collision the smaller ball moves with speed of
A81cm/secB63cm/secC144cm/secDNone of theseThe first ball of mass m moving with a velocity u collides head on with the second ball of mass m at rest. If the coefficient of restitution is e, the ratio of final velocity of the second ball to the initial velocity of the first ball is
A1−e1+eB1+e1−eC1+e2D1−e2
A ball moving with speed v collides with a horizontal smooth surface at an angle θ with normal to surface as shown in figure. If coefficient of restitution of collision is e, then find v'

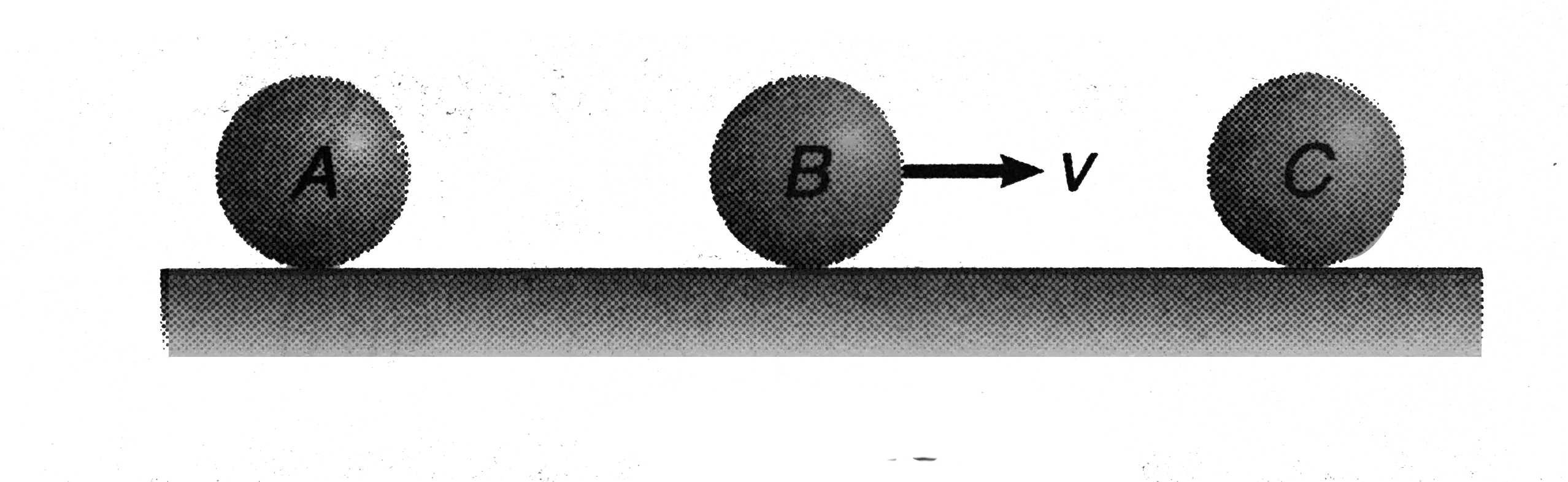
View SolutionThree balls A, B and C are placed on a smooth horizontal surface. Given that mA=mC=4mB. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collisions between the balls. All collisions are elastic.
View SolutionA ball of mass m moving with velocity u strikes another identical ball at rest. Find the velocities of the balls after the collision if the coefficient of restitution is e and the collision is head -on. Also , calculate the loss in K.E.
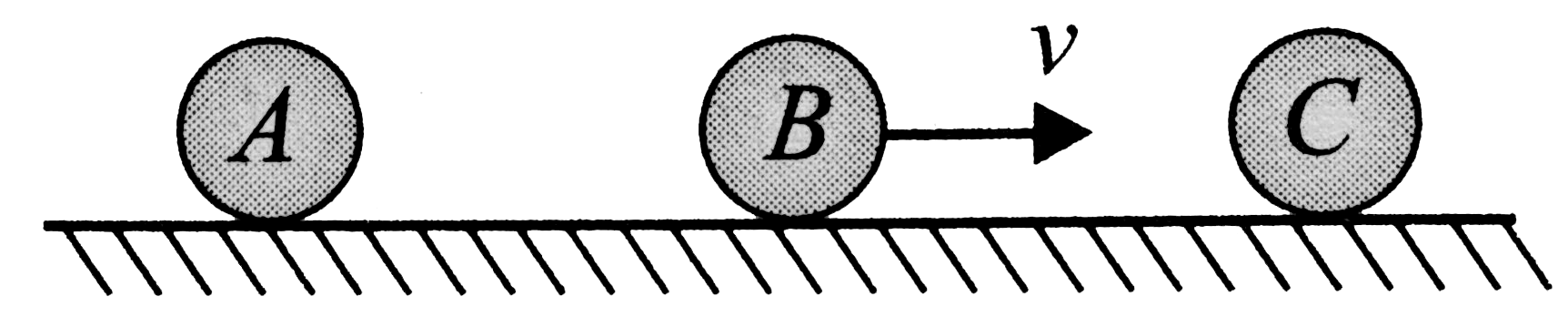
View SolutionThree balls A,B and C(mA=mC=4mB) are placed onn a smooth horizontal surface. Ball B collides with ball C with an initial velocity v as shown in figure. Find the total number of collision betwenent the balls (all collisions are elastic).
View SolutionTwo identical balls are dropped from the same height onto a hard surface, the second ball being released exactly when the first ball bollides with the surface. If the first ball has made two more collisions by the time the second one collides. Then the coefficient of restitution between the ball and the surface satisfies :
View Solution
