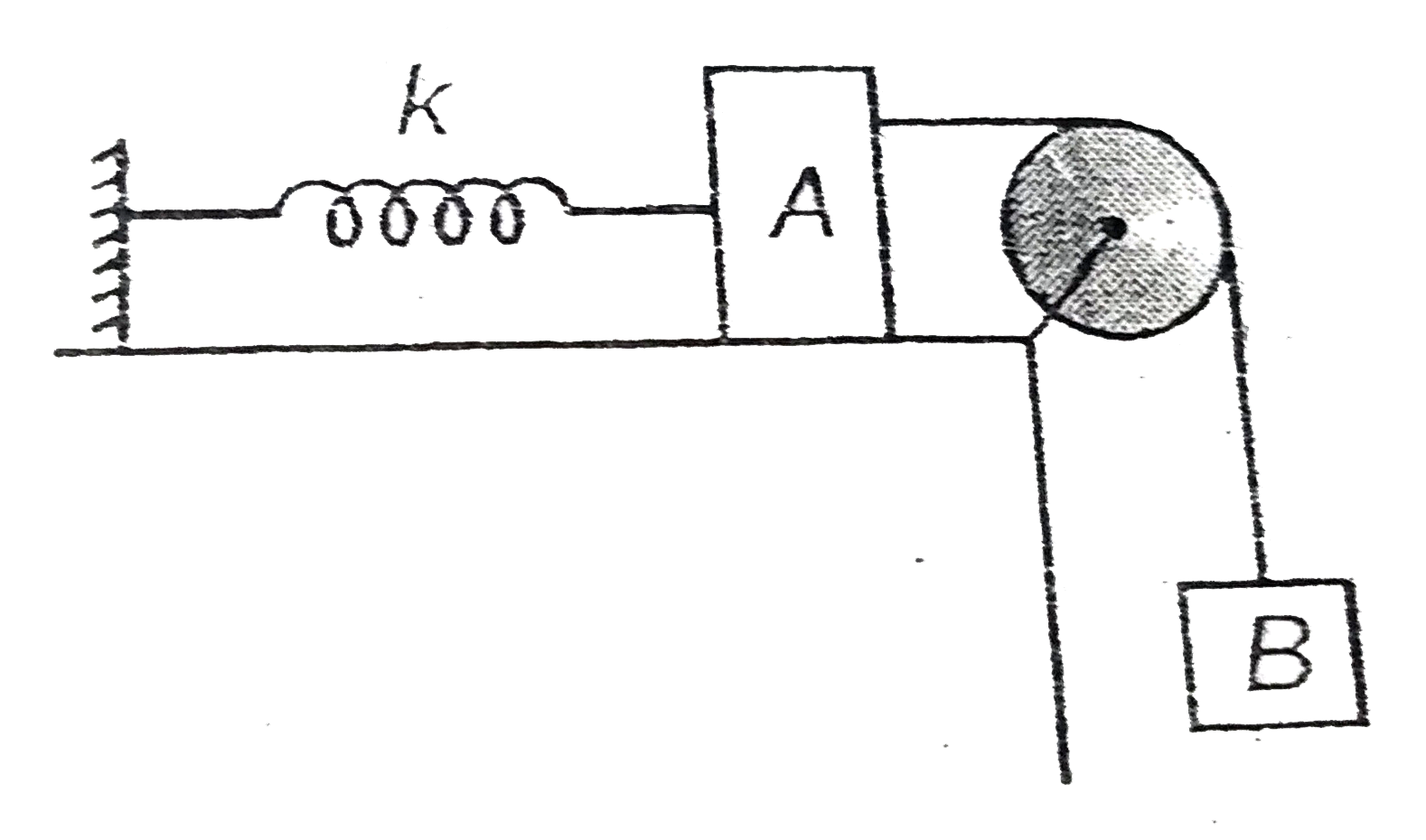
System shown in figure is released from rest . Pulley and spring is massless and friction is absent everywhere. The speed of 5kg block when 2kg block leaves the contact with ground is (force constant of spring k=40N/mandg=10m/s2)

√2m/s
2√2m/s
2m/s
4√2m/s
The correct Answer is:B
Let x be the extension in the spring when 2kg block leaves the constant the contact with ground.
Then, kx=2g
x=2gk=2×1040=12m
Now from conservation of mechanical energy
mgx=12kx2+12mv2 (m=5kg)
v=√2gx−kx2m
Substituting the values
v=√2×10×12−(40)4×5=2√2m/s.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - NEET Questions
49 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
The block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
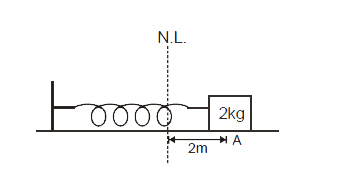
View SolutionIn the figure shown, the system is released from rest with both the springs in unstretched positions. Mass of each block is 1 kg and force constant of each spring is 10 N/m.
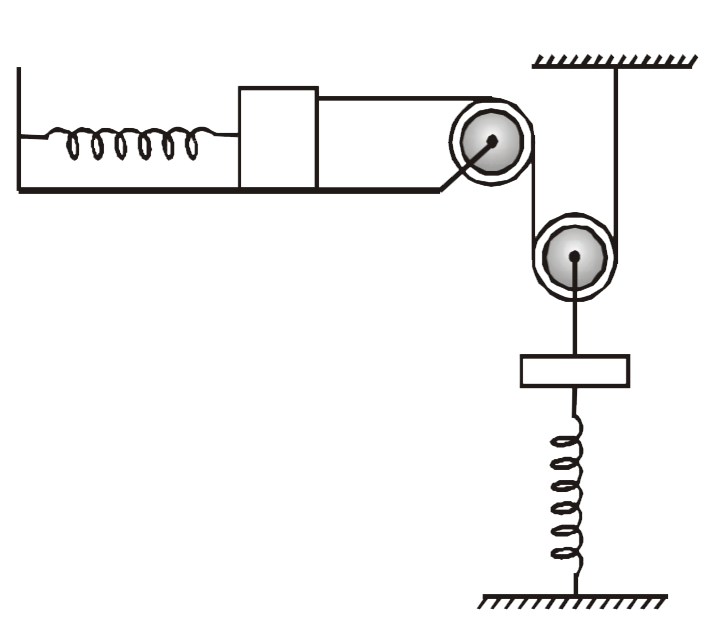
Maximum speed of the block placed horizontally is:
View Solution
Knowledge Check
System shown in figure is released from rest . Pulley and spring is massless and friction is absent everywhere. The speed of 5kg block when 2kg block leaves the contact with ground is (force constant of spring k=40N/mandg=10m/s2)
 A√2ms−1B2√2ms−1C2ms−1D4√2ms−1
A√2ms−1B2√2ms−1C2ms−1D4√2ms−1In the system shown in figure mB=4kg , and mA=2kg . The pulleys are massless and friction is absent everywhere. The acceleration of block A is.
 A10/3m/s2B20/3m/s2C2m/s2D4m/s2
A10/3m/s2B20/3m/s2C2m/s2D4m/s2From the fixed pulley, masses 2 kg, 1 kg and 3 kg are suspended as shown is figure. Find the extension in the spring when acceleration of 3 kg and 1 kg is same if spring constant of the spring k = 100 N/m. (Take g=10ms−2)
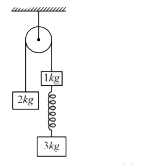 A10 cmB20 cmC30 cmD25 cm
A10 cmB20 cmC30 cmD25 cm
A block of mass 10kg is placed on a horizontal surface as shown in the figure and a force F=100N is applied on the block as shown, in the figure. The block is at rest with respect to ground. If the contact force between block and ground is 25n (in Newton) then value of n is : (Takeg=10m/s2)

View SolutionA planck of mass 5kg is placed on a frictionless horizontal plane. Further a block of mass 1kg is placed over the plank. A massless spring of natural length 2m is fixed to the plank by its one end. The other end of spring is compressed by the block by half of spring's natural length. They system is now released from the rest. What is the velocity of the plank when block leaves the plank? (The stiffness constant of spring is 100N/m)

View SolutionA block of mass 1 kg is released on wedge from position M as shown in figure (Neglect friction everywhere). The force exerted by vertical wall W on wedge, when the block is at position N is 152√P newton, then what is the value of P (Take g = 10 m/s2)?
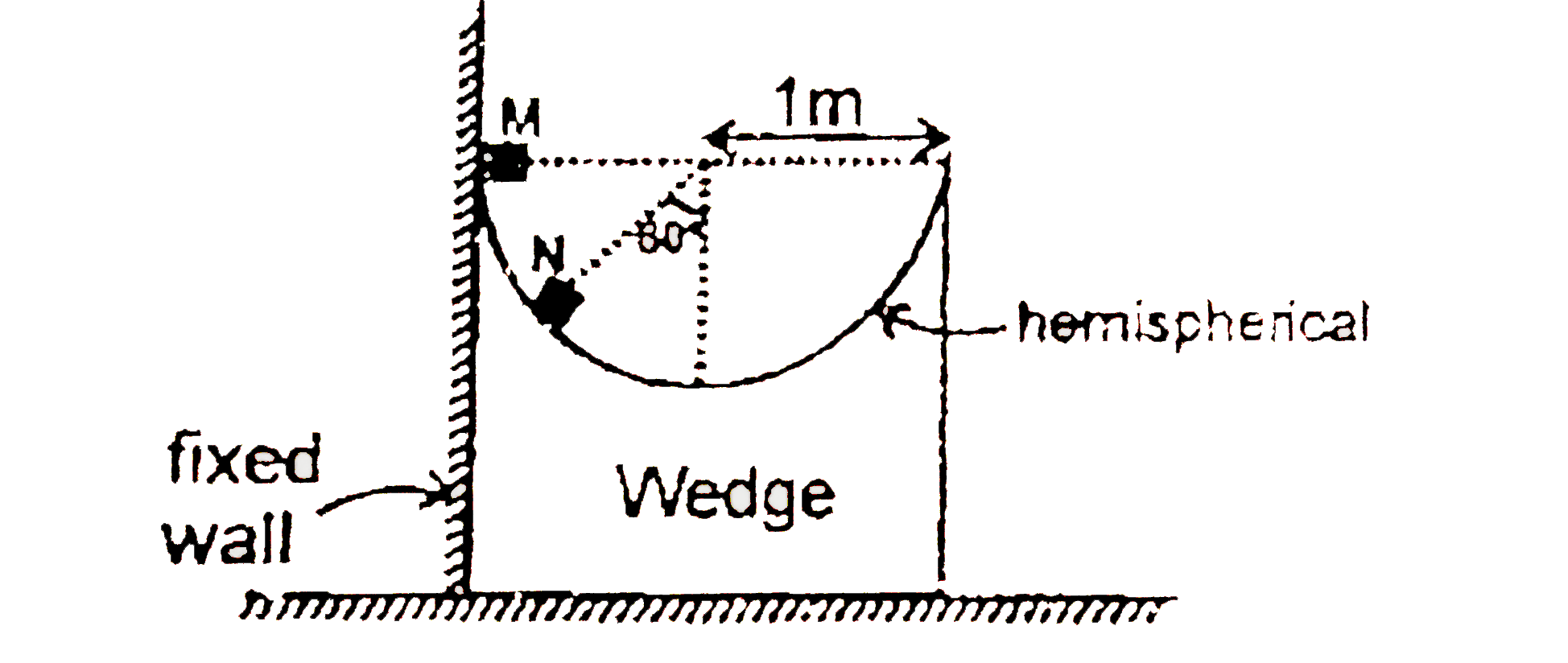
View SolutionConsider the situation shown in figure.
Mass of block A is m and that of blcok B is 2m. The force constant of string is k. Friction is absent everywhere. System is released from rest with the spring unstretched. Find
(a) The maximum extension of the spring xm
(b) The speed of block A when the extension in the springt is x=xm2
(c ) The net acceleration of block B when extension in the spring is x=xm4.
View SolutionA 2kg block in on 5 kg block. The system of blocks falls freely due to gravity as shown. The net force on 5 kg block is:
(Takeg=10m/s2)

View Solution
