A simple pendulum of length hangs from a horizontal roof as shown in figure. The bob of mass is given an initial horizontal velocity of magnitude as shown in figure. The coefficient of restitution . After how many collisions the bob shall no long come into constant with the horizonrtal roof?
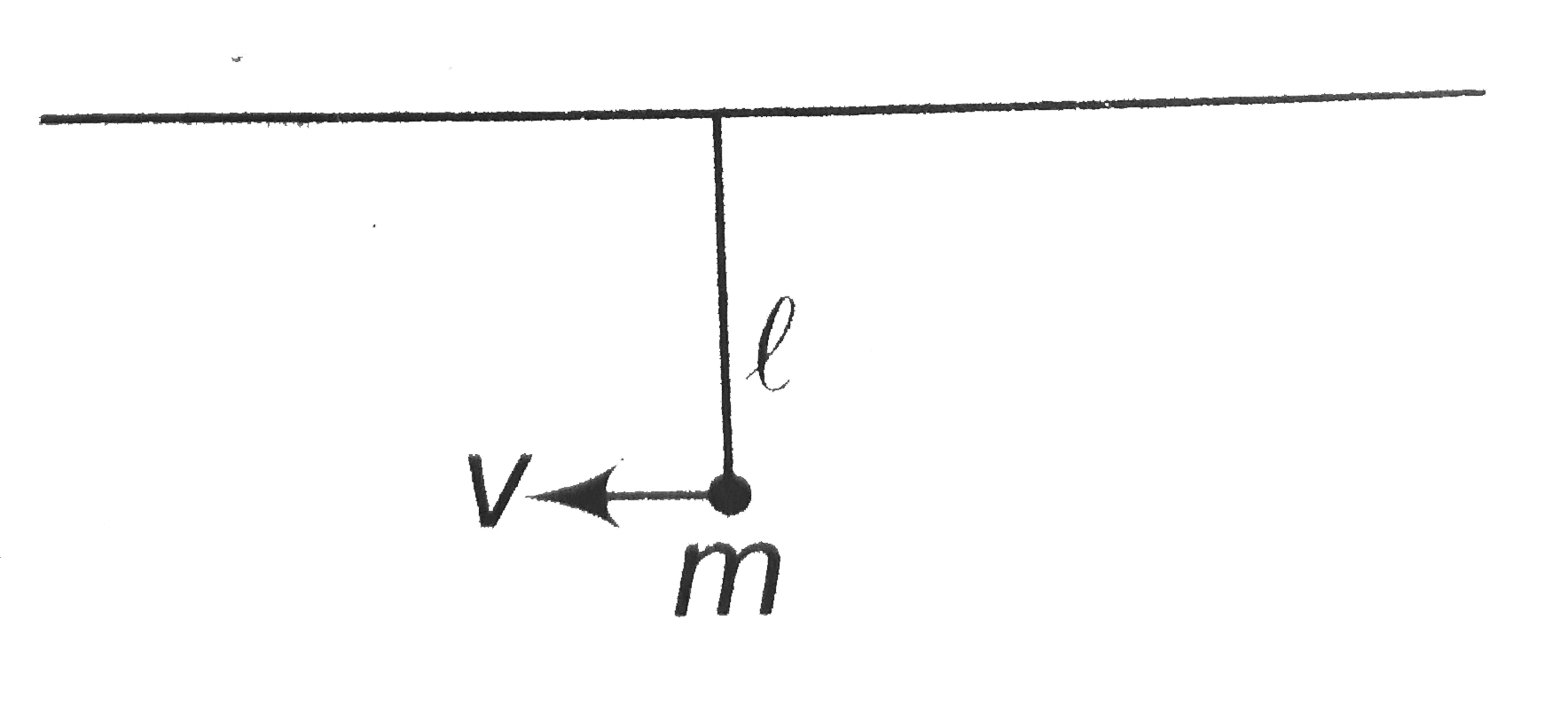
1
2
4
none of these
The correct Answer is:A
After the collision with horizontal roof:
The speed of the both after collision the speed of the bob before collision
At the highest point the bob has sufficient potential energy to again rise to the level of horizontal roof. Even if the speed of the bob is reduced to zero as a result of collision (after infinite collision), the bob has sufficient potential energy to again rise t the level to horizontal roof.
Hence the required number of collision are infinite.
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - NEET Questions
49 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Collision
31 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
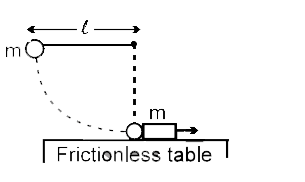
The bob of a simple pendulum of length l dropped from a horizontal position strikes a block of the same mass, placed on a horizontal table (frictionless) as shown in the diagram, the block shall have kinetic energy-
View SolutionA simple pendulum is supended from a peg on a verticl wall. The pendulum is pulled away from the wall to a horizontal position and releases as shown in figure −4.152. The ball hits the wall, the coefficient of restitution being 2/√2. What is the minimum number of collisions after which the amplitude of oscillation becomes less than 60∘
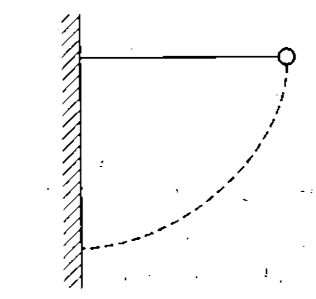
View Solution
Knowledge Check
A simple pendulum is hanging from a peginserted in a vertical wall. Its bob is strteched to horizontal position form wall and left freee to move, the bob hits the wall. If coefficient of restitution is 2√5. After how many collisions the amplitude of vibration will becomes less then 60∘.
A6B3C5D4A simple pendulum is hanging from a peg inserted in a vertical wall. Its bob is stretched in horizontal position from the wall and is left free to move. The bob hits on the wall the coefficient of restitution After how many collsions the amplitude of vibration will become less than 60∘
A6B3C5D4A long block A is at rest on a smooth horizontal surface. A small block B whose mass is half of mass of A is placed on A at one end and is given an initial velocity u as shown in figure. The coefficient of friction between the blocks is μ.
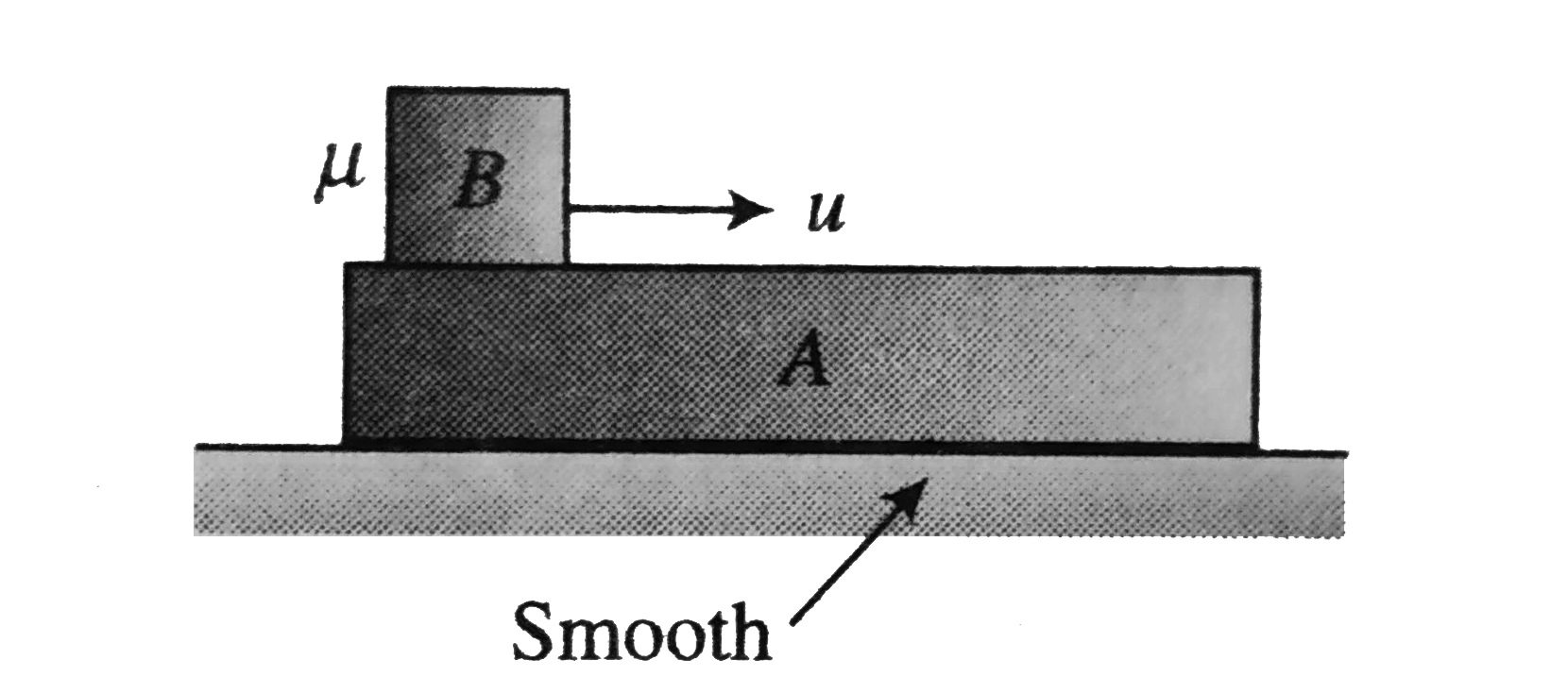A(a) Finally both move with a common velocity 2u/3.B(b) Acceleration of B relative to A initially is 3μg/2 towards left.C(c) Magnitude of total work done by friction is equal to the final kinetic energy of the system.D(d) The ratio of initial to final momentum of the system is 1.
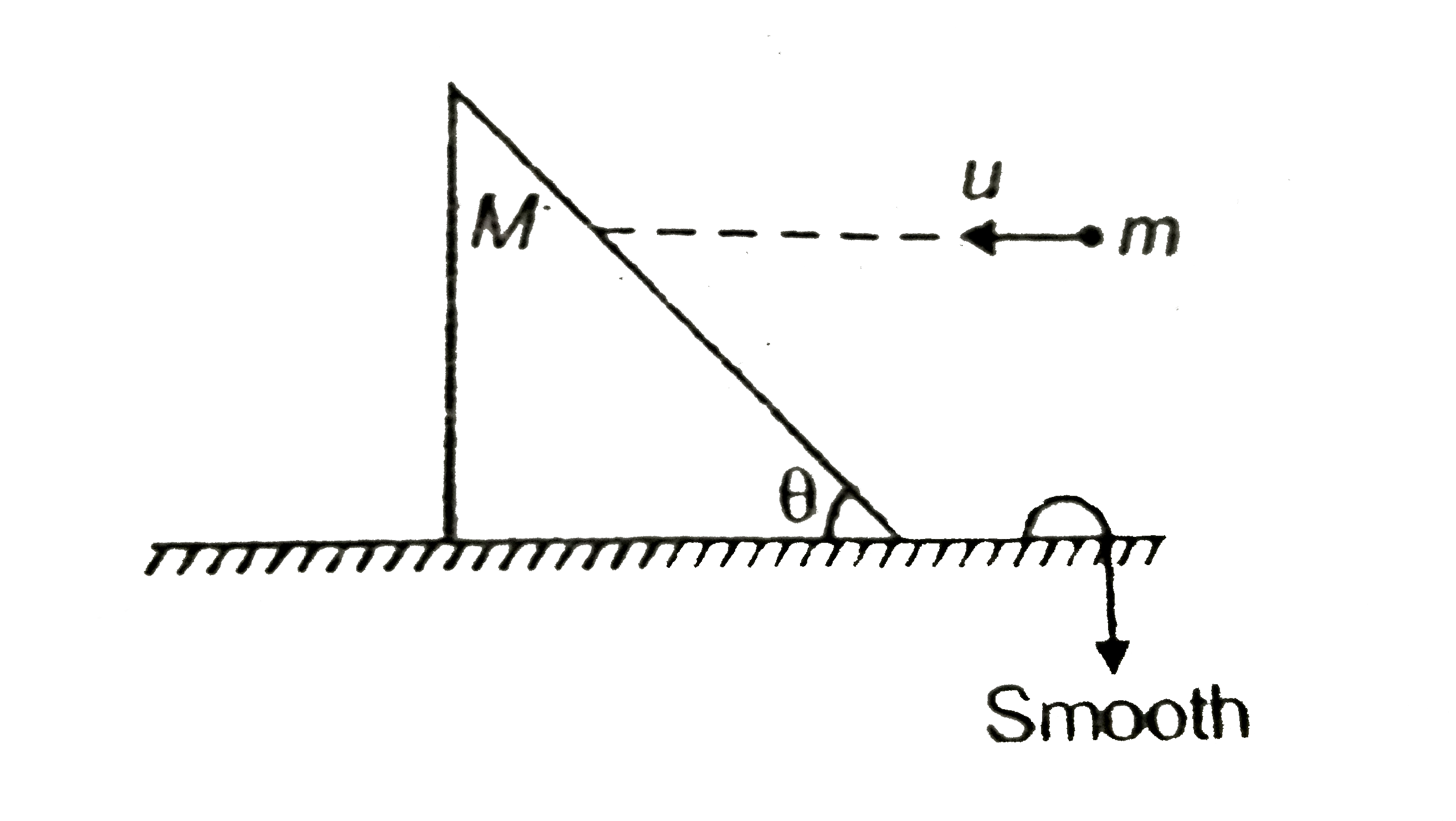
A particle of mass m moving with speed u hits a wedge of mass M as shown in figure. If coefficient of restitution is e and friciton can be neglected, then find the speed of the wedge with respect to ground just after the collision.
View SolutionBall 1 collides with an another identical ball 2 at rest as shown in figure. For what value of coefficient of restitution e, the velocity of ball 2 becomes two times that of ball I after collision?
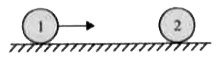
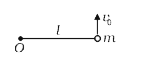
View SolutionA bob in tied to a string of length l & and kept on a horizontal rough surface as shown in the figure when point O of the string is fixed. The bob is given a tangential velocity V0 keeping the string taut as shown in figure. Find the tension in the string as a function of time. The coefficient of kinetic friction is μ.
View SolutionA ball of mass 1kg is dropped from a height of 3.2m on smooth inclined plane. The coefficient of restitution for the collision is e=1/2. The ball's velocity become horizontal after the collision.
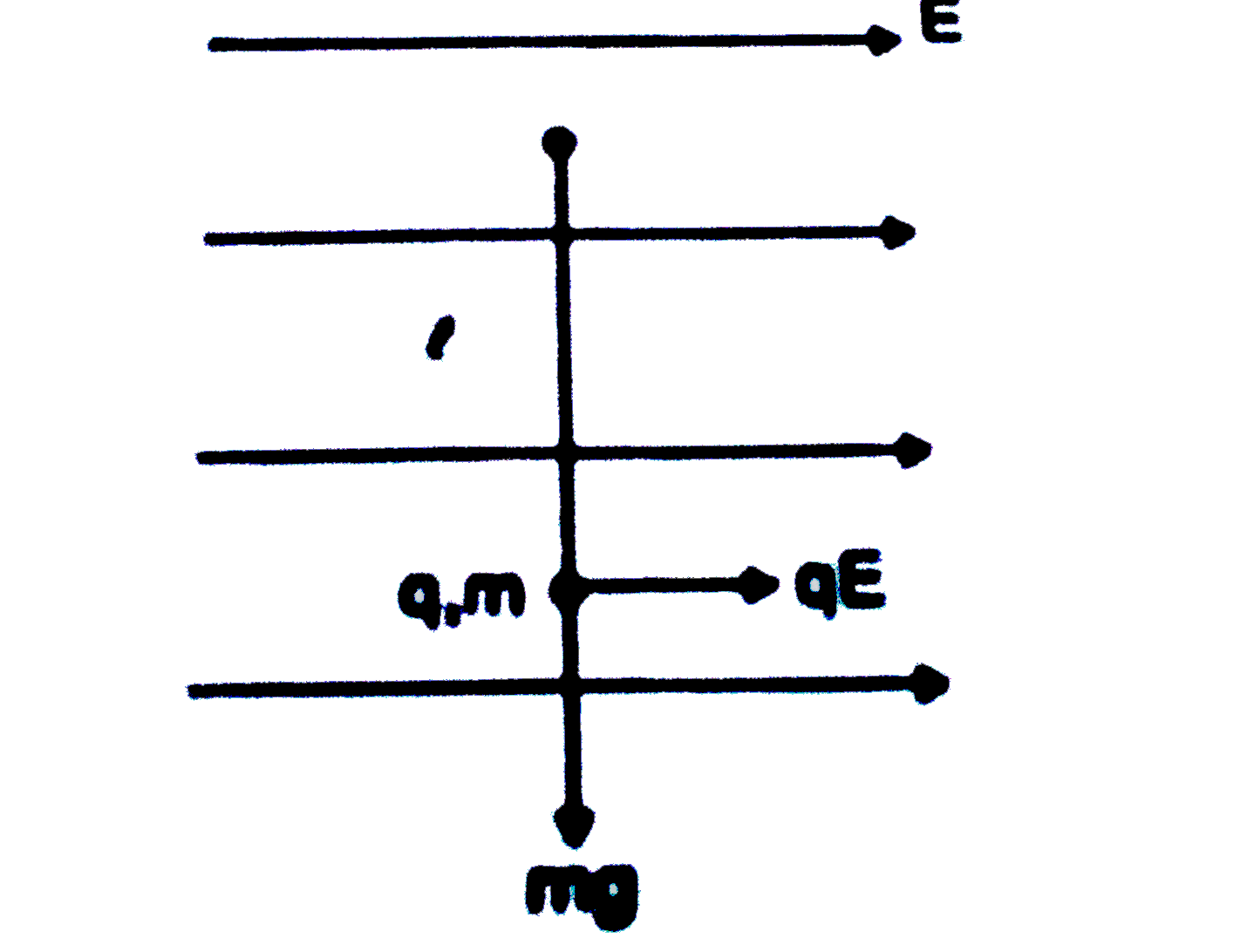
View SolutionA simple pendulum has a length l & mass of bob m. The bob is given a charge q coulomb. The pendulum is suspended in a uniform horizontal electric field of strength E as shown in figure, then calculate the time period of oscillation when bob is slightly displaced from its mean position.
View Solution