A mass m moving horizontal (along the x-axis) with velocity v collides and stricks to mass of 3m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is
14vˆi+32vˆj
13vˆi+23vˆj
23vˆi+13vˆj
32vˆi+14vˆj
To solve the problem of finding the final velocity of the combined mass after the collision, we can follow these steps:
Step 1: Identify the masses and their velocities
- Mass m is moving horizontally along the x-axis with velocity v.
- Mass 3m is moving vertically upward along the y-axis with velocity 2v.
Step 2: Determine the initial momentum of each mass
- The momentum of mass m moving along the x-axis is given by:
px=m⋅v^i
- The momentum of mass 3m moving along the y-axis is given by:
py=3m⋅2v^j=6mv^j
Step 3: Calculate the total initial momentum
The total initial momentum →Pinitial can be expressed as:
→Pinitial=px+py=mv^i+6mv^j
Step 4: Determine the total mass after the collision
After the collision, the two masses stick together. The total mass M is:
M=m+3m=4m
Step 5: Apply the conservation of momentum
According to the conservation of momentum, the total initial momentum is equal to the total final momentum:
→Pinitial=→Pfinal
Let the final velocity of the combined mass be →Vfinal. Thus:
→Pfinal=M⋅→Vfinal=4m⋅→Vfinal
Step 6: Set the initial momentum equal to the final momentum
Setting the total initial momentum equal to the total final momentum:
mv^i+6mv^j=4m⋅→Vfinal
Step 7: Solve for the final velocity
Dividing both sides by 4m:
→Vfinal=mv^i+6mv^j4m
This simplifies to:
→Vfinal=v4^i+6v4^j=v4^i+3v2^j
Final Answer
The final velocity of the combined mass after the collision is:
→Vfinal=v4^i+3v2^j
- Mass m is moving horizontally along the x-axis with velocity v.
- Mass 3m is moving vertically upward along the y-axis with velocity 2v.
- The momentum of mass m moving along the x-axis is given by:
px=m⋅v^i
- The momentum of mass 3m moving along the y-axis is given by:
py=3m⋅2v^j=6mv^j
The total initial momentum →Pinitial can be expressed as:
→Pinitial=px+py=mv^i+6mv^j
After the collision, the two masses stick together. The total mass M is:
M=m+3m=4m
According to the conservation of momentum, the total initial momentum is equal to the total final momentum:
→Pinitial=→Pfinal
Let the final velocity of the combined mass be →Vfinal. Thus:
→Pfinal=M⋅→Vfinal=4m⋅→Vfinal
Setting the total initial momentum equal to the total final momentum:
mv^i+6mv^j=4m⋅→Vfinal
Dividing both sides by 4m:
→Vfinal=mv^i+6mv^j4m
This simplifies to:
→Vfinal=v4^i+6v4^j=v4^i+3v2^j
The final velocity of the combined mass after the collision is:
→Vfinal=v4^i+3v2^j
Topper's Solved these Questions
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - AIIMS Questions
20 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test
29 Videos
- WORK, ENERGY, POWER AND COLLISIONBOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Assertion Reasoning
17 Videos
- WAVES AND ACOUSTICSBOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test
30 Videos
Similar Questions
Particle A of mass mA=m2 moving along the x - axis with velocity v0 collides elastically with another particle B at rest having mass mB=m3 . If both particles move along the x - axis after the collision , the change Δλ in de - Broglie wavelength of particle A , in terms of its de - Broglie wavelength (λ0) before collision is :
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View Solution
Knowledge Check
A mass m moving horizontally (along the x-axis) with velocity v collides and stricks to a mass of 3 m moving vertically upward (along the y-axis) with velocity 2v. The final velocity of the combination is
A32vˆi+14vˆjB14vˆi+32vˆjC13vˆi+23vˆjD23vˆi+13vˆjA body A of mass 5kg is moving along the x-axis with a velocity 2m/s. Another body (B) of mass 10 kg is moving along the y-axis with a velocity √3m/s. They collide at the origin and stick together. What is the final velocity of the combined mass?
A√3m/sB(√3+1)m/sC43m/sD2(√3+1)m/sA ball of mass m moving with velocity v collides elastically with another ball of identical mass coming from the opposite direction with velocity 2v. Their velocities after collisions are-
A−v,2vB−2v,vCv,−2vD2v,−v
A particle of mass m moving with speed v in position x - direction collides perfectly inelastically with another identical particle moving with same speed in positive y - direction . Find final velocity of the combination.
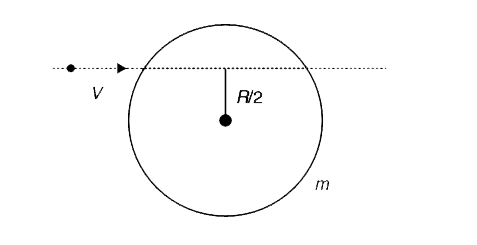
View SolutionA disc of mass m and radius R lies flat on a smooth horizontal table. A particle of mass m, moving horizontally along the table, strikes the disc with velocity V while moving along a line at a distance R2 from the centre. Find the angular velocity acquired by the disc if the particle comes to rest after the impact.
View SolutionA ball of mass in m=1kg is hung vertically by a thread of length l=1.50m. Upper end of the thread is attached to the ceiling of a trolley of mass M=4kg. Initially, the trolley is stationary and it is free to move along horizontal rails without friction. A shell of mass m=1 kg, moving horizontally with velocity v0=6m/s collides with the ball and gets stuck with it. As a result, the thread starts to deflect towards right.
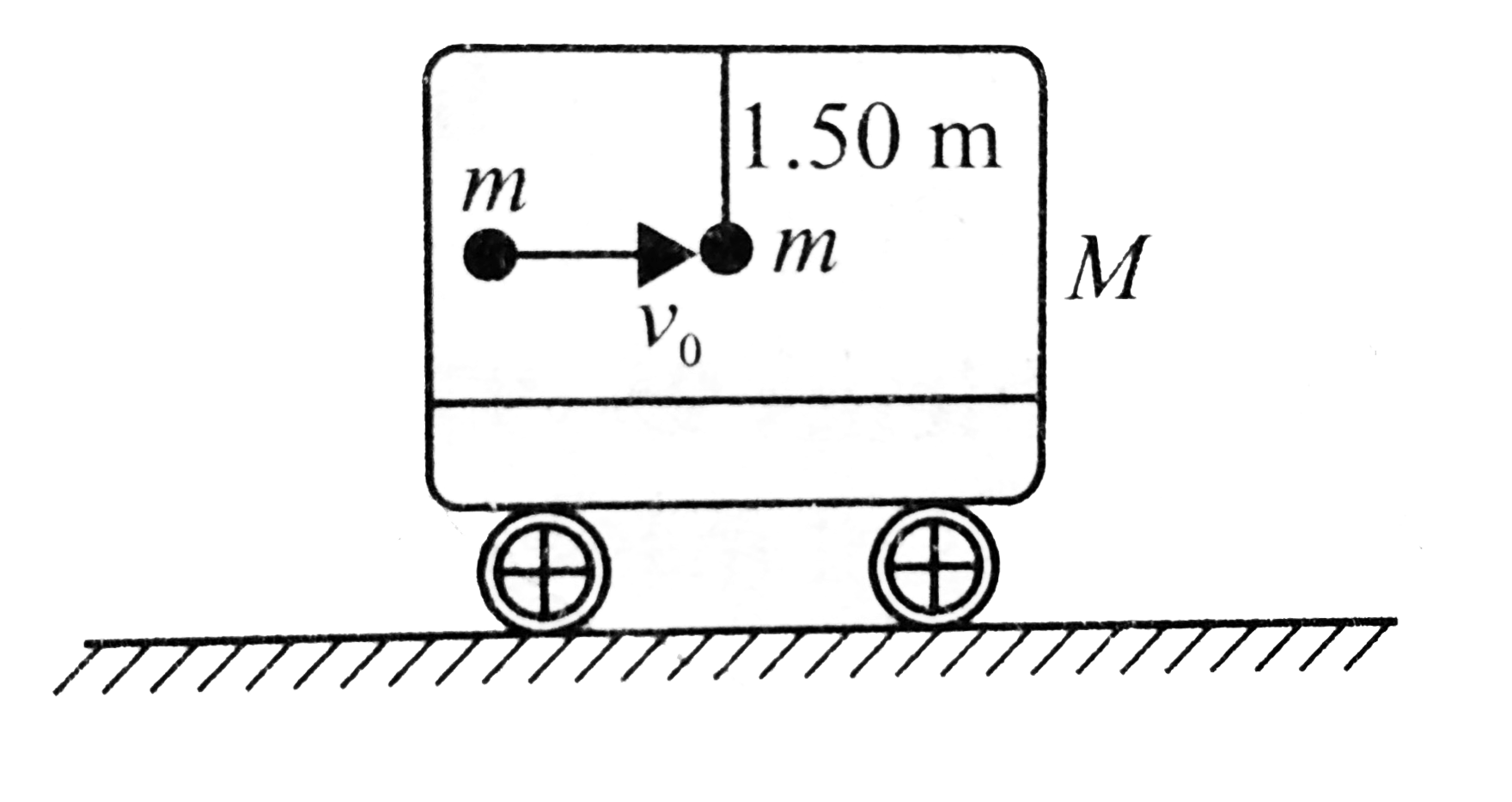
The velocity of the combined body just after collision is
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionA body of mass 20 kg is moving with a velocity of 2v and another body of mass 10 kg is moving with velocity V along same direction. The velocity of their centre of mass is
View Solution
