The potential energy of a partical veries with distance x as shown in the graph.
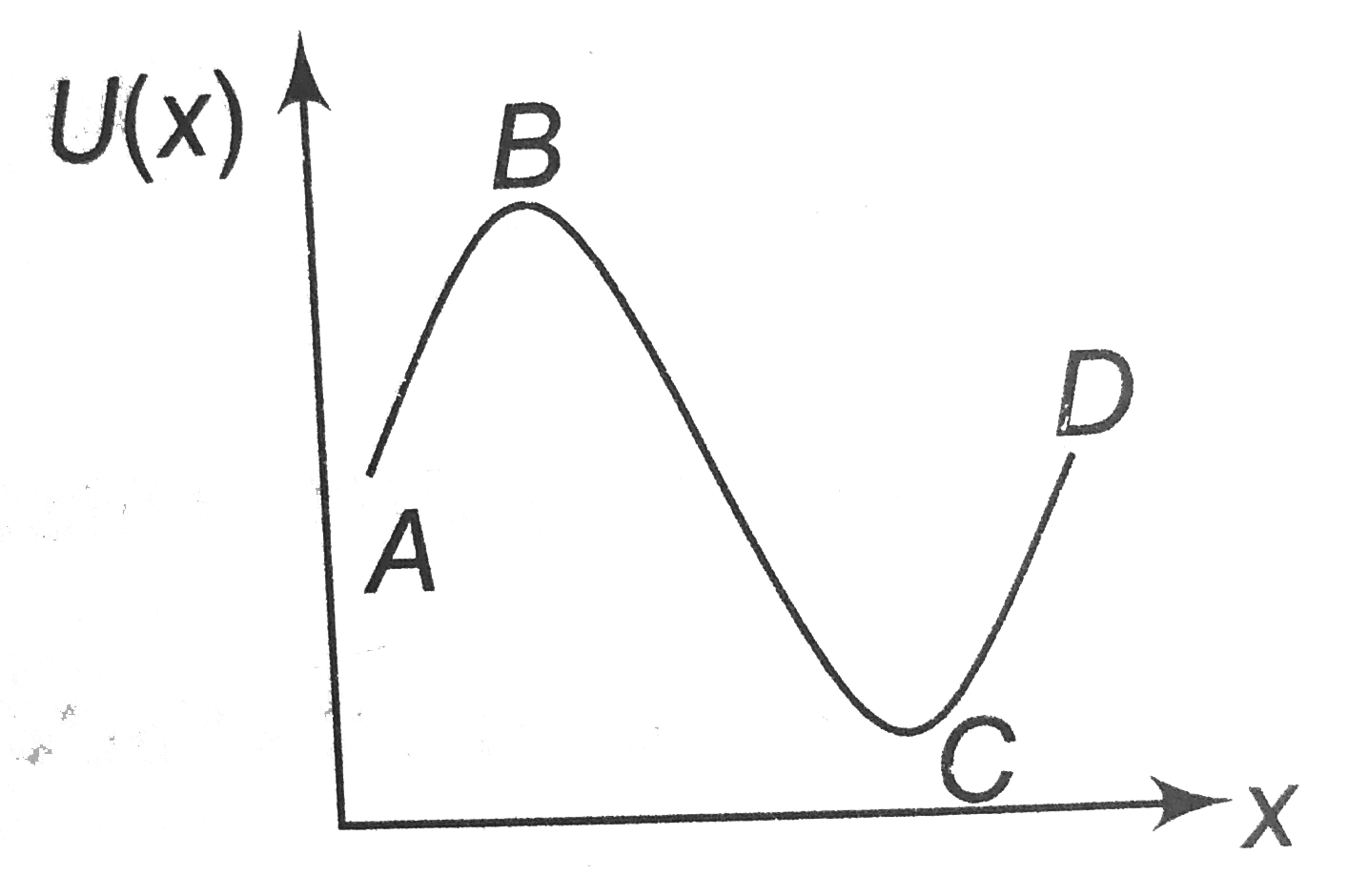
The force acting on the partical is zero at
C
B
B and C
A and D
F=−dUdx it is clear that slop of U−x curve is zero at point BandC
Topper's Solved these Questions
Similar Questions
The potential energy of a partical varies as
. U(x)=E0for0≤x≤1 =0forx>1For0≤x≤1, de- Broglie wavelength is λ1 and for xgt the de-Broglie wavelength is λ2. Total energy of the partical is 2E_0. find λ1λ2.
View SolutionThe potential energy of a partical is SHM is 2×10−4 J at the extreme positions. What will be its potential energy when the particle is midway between the mean and extreme position ?
View Solution
Knowledge Check
The potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
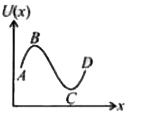 ACBBCB and CDA and D
ACBBCB and CDA and DThe potential energy of a particle varies with distance x as shown in the graph. The force acting on the particle is zero at
 ACBBCB and CDA and D.
ACBBCB and CDA and D.force F on a partical moving in a straight line veries with distance d as shown in the figure. The work done on the partical during its displacement of 12m is
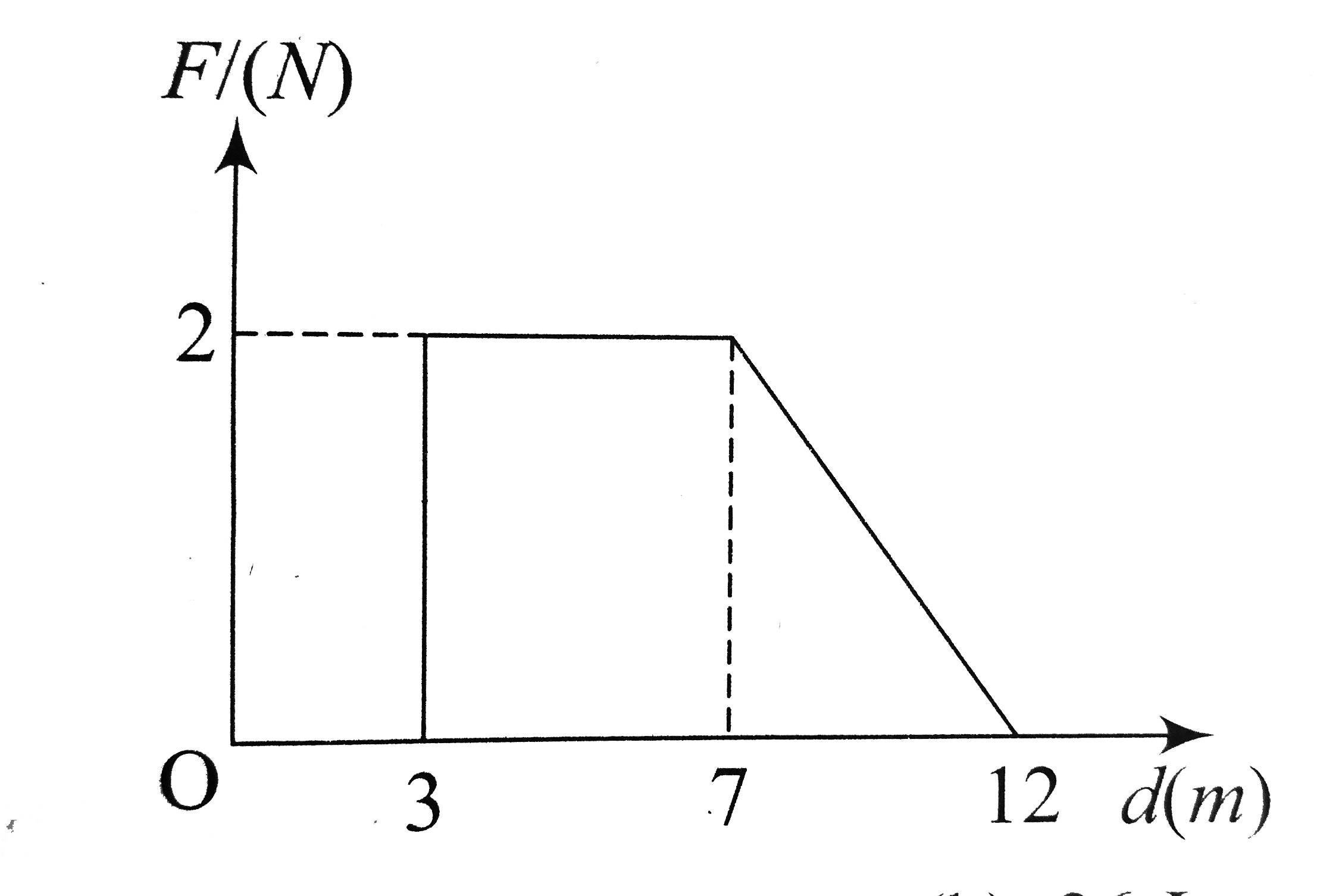 A21JB26JC13JD18J
A21JB26JC13JD18J
The potential energy ‘V’ of a particle moving along the positive x-direction in a conservative force field varies as shown in the figure. The total energy is E=2. Draw the corresponding kinetic energy K vs x graph.
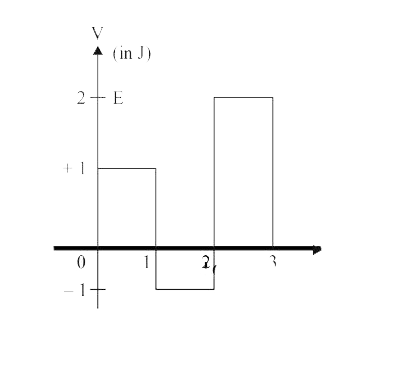
View SolutionA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
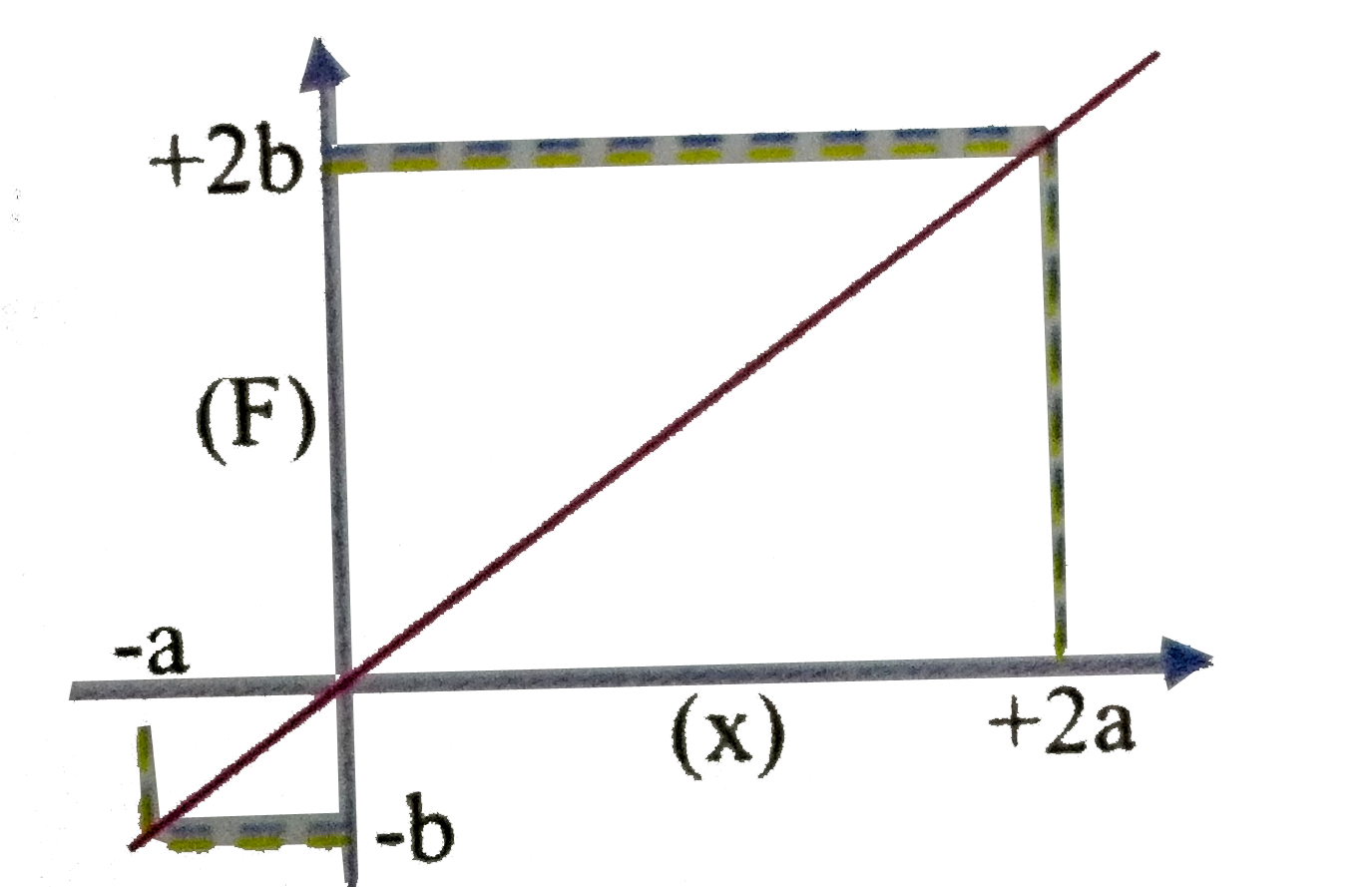 .
.
View SolutionThe variation of potential energy U of a system is shown in figure. The force acting on the system is best represented by
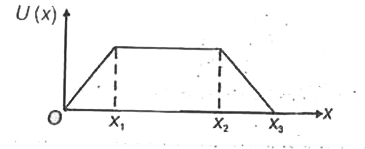
View SolutionThe potential energy of a body is given by U=A−Bx2 (where x is the displacement). The magnitude of force acting on the partical is
View SolutionAssertion: The change in kinetic energy of a partical is equal to the work done on it by the net force.
Reason: Change in kinetic energy of partical is equal to the work done in case of a system of one partical.
View Solution
