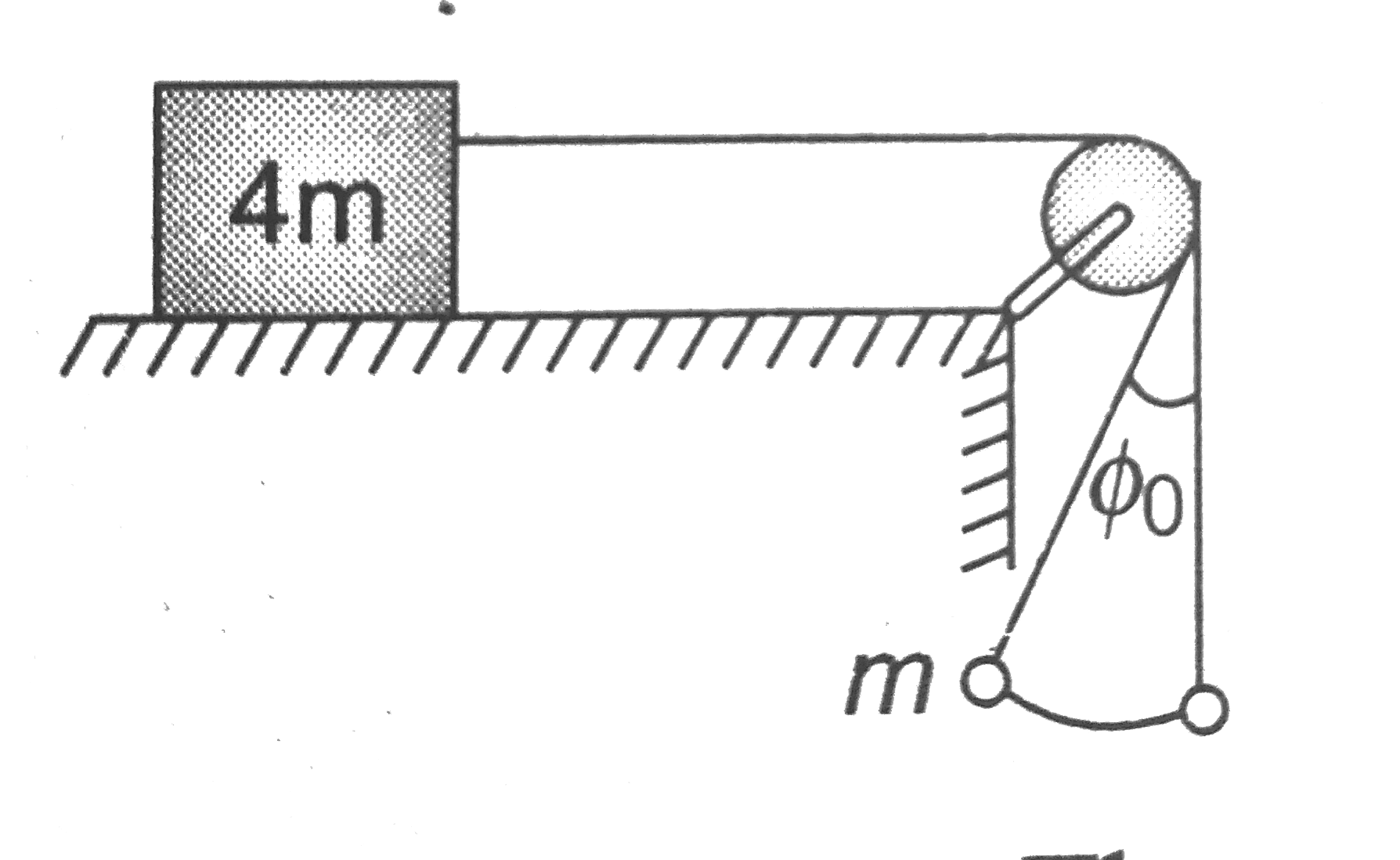
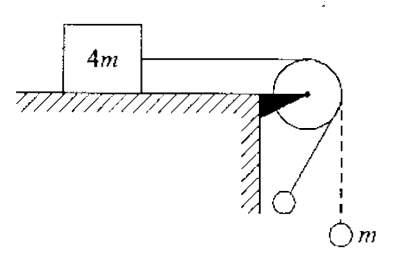
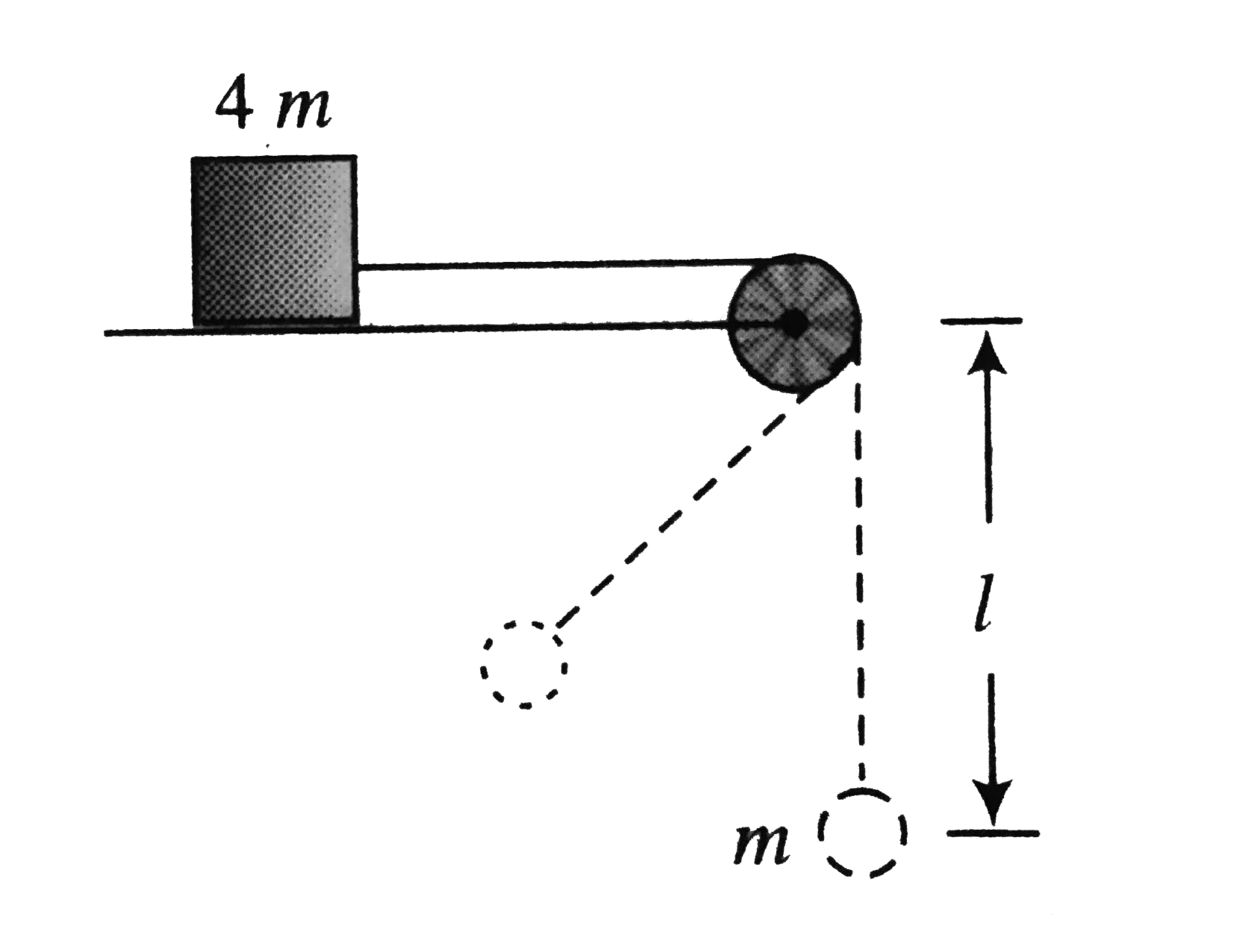
Two bodies of mass m and 4m are attached with string of length l is excurting oscillations of angular amplitude θ0 while the other body is at rest . The minimum coefficient of friction between the mass 4m and the horizontal surface should be:
(2−cosθ03)
2cos2(θ02)
(1−cosθ02)
(3−cosθ04)
Maximum tension in the string is in its lowest position.
∴ Speed of mass m in its lowest position is
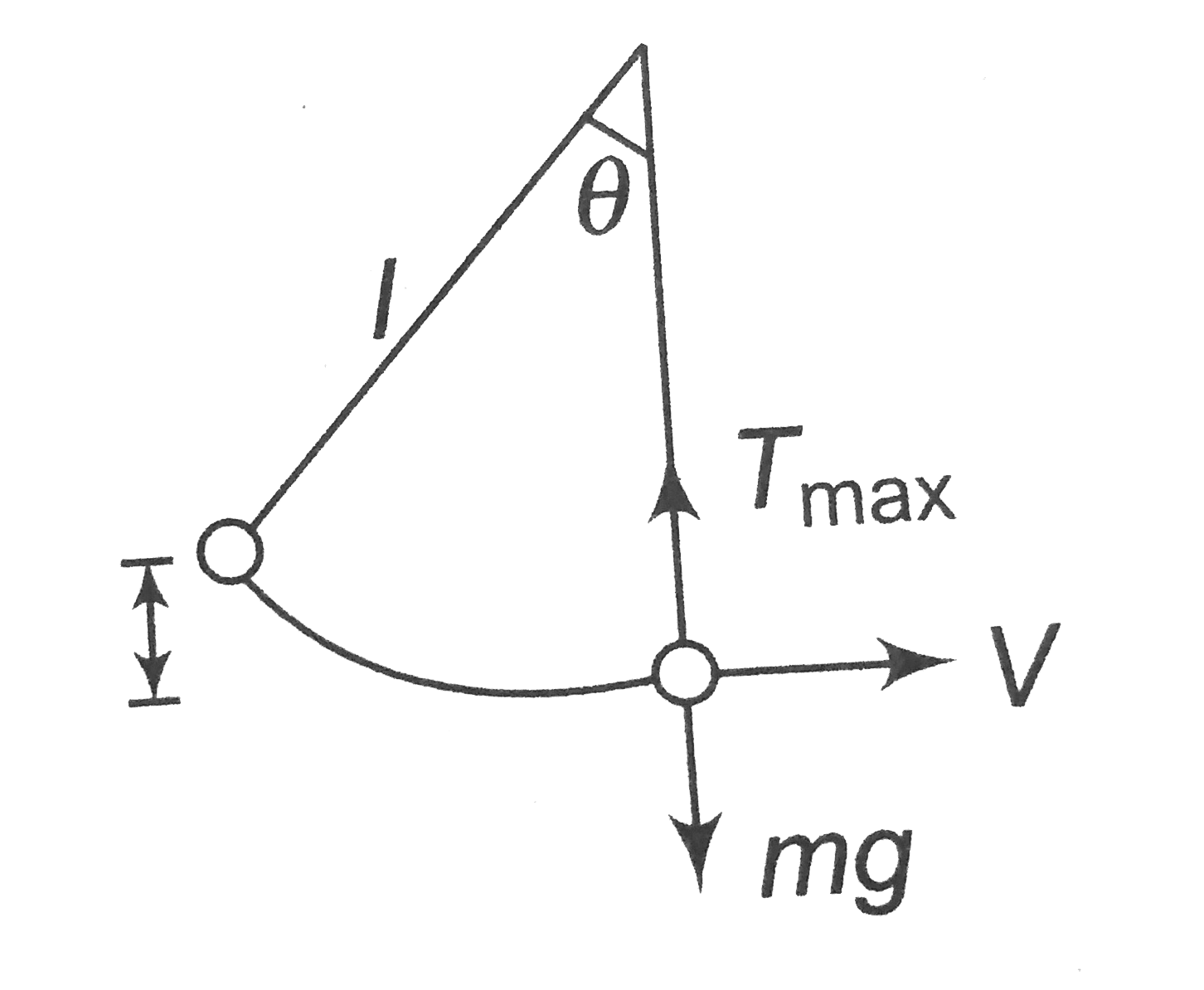
v2=2gh=2hl(1−cosθ)
Tmax−mg=mv2l
Tmax−mg+2mg(1−cosθ)
=mg(3−cosθ)
Block of mass 4m does not move.
So μ(4mg)≥Tmax
or 5μmg≥mg(3−cosθ)orμ≥(3−cosθ04)
Topper's Solved these Questions
Similar Questions
Shown in the diagram is a system of two bodies, a block of mas m and a disc of mass M, held in equilibrium. If the string 3 is burnt, find the acceleration of the disc. Neglect the masses of the pulleys P and Q. (The coefficient of friction between the block and horizontal surface is μ)
 View Solution
View SolutionTwo blocks A and B of respective masses 6 kg and 4 kg are connected with a string passing over a light friction less pulley as shown in the figure . The coefficient of friction between the block A and horizontal surface is 0.4 . Then the minimum mass of block C which should be placed over A to prevent it from moving is :
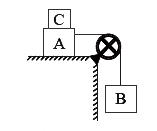 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
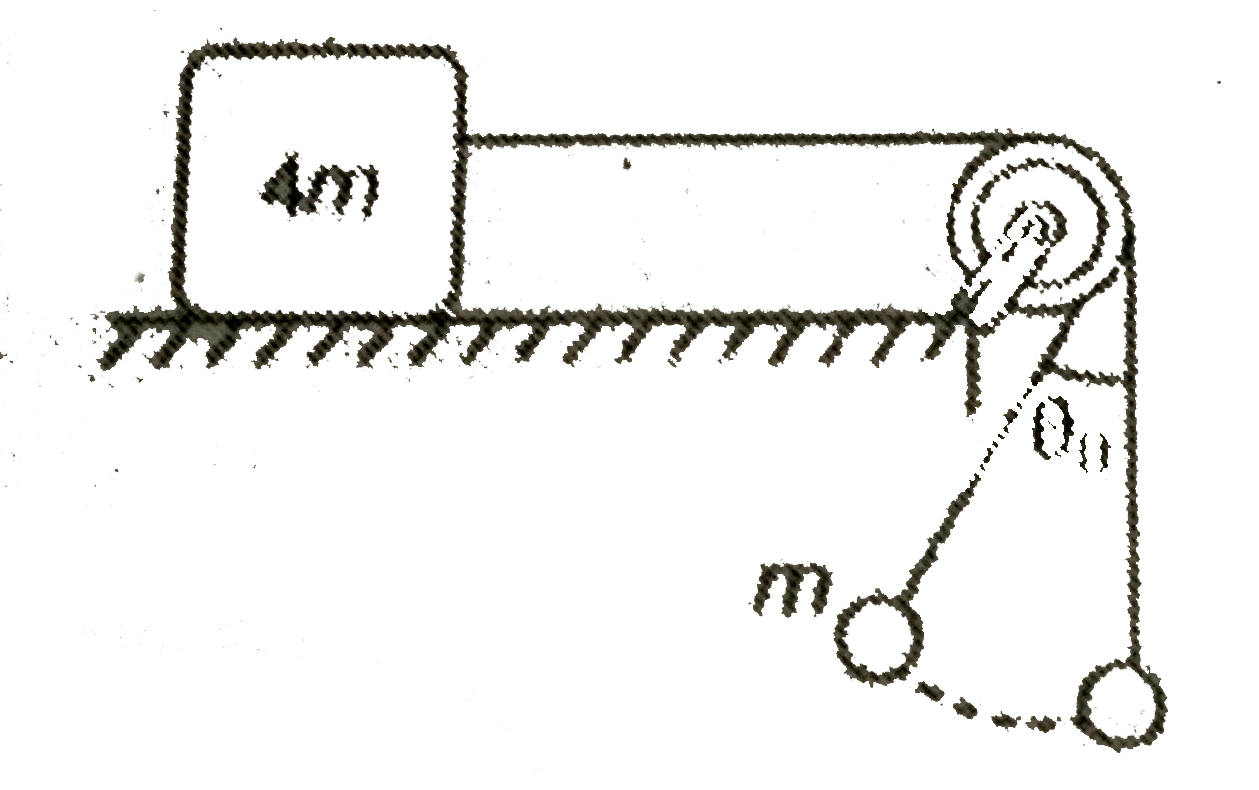
Two bodies of masses m and 4 m are attached with string as shown in the figure. The body of mass m hanging from a string of length l is executing oscillations of angular amplitude θ0 while the other body is at rest. The minimum coefficient of friction between the mass 4m and the horizontal surface should be
 A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04)
A(2−cosθ03)B2cos2(θ02)C(1−cosθ02)D(3−2cosθ04) - Question 2 - Select One
Two bodies of mass m and 4m are attached by a string shown in the figure-2.146. The body of mass m hanging from a string of length l is executing simple harmonic motion with amplitude A while other body is at rest on the surface. The minimum coefficient of friction between the mass 4m and the horizontal surface must be to keep it at rest is :
 A14(1−A2l2)B14(1+A2l2)C14AlcosθD14
A14(1−A2l2)B14(1+A2l2)C14AlcosθD14 - Question 3 - Select One
Two bodies of masses m and 4m are attached to a light string as shown in figure. A body of mass m hanging from string is executing oscillations with angular amplitude 60∘, while other body is at rest on a horizontal surface. The minimum coefficient of friction between mass 4m and the horizontal surface is (here pulley is light and smooth)
 A(a) 14B(b) 34C(c) 12D(d) 18
A(a) 14B(b) 34C(c) 12D(d) 18
In the arrangement of figure the masses m0, m1, and m2 of bodies are equal, the masses of the pulley and the threads are negligible, and there is no friction in the pulley. Find the acceleration w with which the body m0 comes down, and the tension of the thread binding together the bodies m1 and m2, if the coefficient of friction between these bodies and the horizontal surface is equal to k. Consider possible cases.
 View Solution
View SolutionTwo blocks of masses M1=4 kg and M2=6kg are connected by a string of negligible mass passing over a frictionless pulley as shown in the figure below. The coefficient of friction between the block M1 and the horizontal surface is 0.4. when the system is released, the masses M1 and M2 start accelrating. What additional mass m should be placed over M1 so that the masses (M1+m) slide with a uniform speed?
 View Solution
View SolutionTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
View SolutionTwo bodies of masses m and M are attached to the two ends of a light string passing over a fixed ideal pulley (M>>m). When the bodies are in motion, the tension in the string is approximately
View SolutionTwo blocks of masses m1 and m2 are connected by a spring having spring constant K. Initially , the spring is at its natural length. The coefficient of friction between the blocks and the surface is μ. What minimum constant force has to be applied in the horizontal direction to the block of mass m1, in order to shift the other block ?
View Solution

