Three identical thin rods each of length and mass are joined together to from a letter. . What is the moment of inertia of the system about one of the sides of ?
The correct Answer is:D
To find the moment of inertia of the system formed by three identical thin rods arranged in the shape of the letter "H" about one of the sides (let's say side AB), we can follow these steps:
Step 1: Identify the rods and their arrangement
We have three rods:
- Rod AB (vertical)
- Rod CD (horizontal)
- Rod EF (horizontal)
Step 2: Calculate the moment of inertia of rod CD about AB
Rod CD is perpendicular to rod AB. The moment of inertia I of a rod about an axis through one end and perpendicular to its length is given by the formula:
I=13ML2
For rod CD:
ICD=13Ml2
Step 3: Calculate the moment of inertia of rod EF about AB
Rod EF is parallel to rod AB and is at a distance l from it. The moment of inertia I of a rod about an axis parallel to it and at a distance d is given by the parallel axis theorem:
I=Icm+Md2
where Icm is the moment of inertia about its center of mass. For rod EF:
Icm=13Ml2
The distance d from AB to EF is l:
IEF=13Ml2+M(l)2=13Ml2+Ml2=13Ml2+33Ml2=43Ml2
Step 4: Total moment of inertia about AB
Now, we can find the total moment of inertia Itotal about the axis through AB:
Itotal=ICD+IEF=13Ml2+43Ml2=53Ml2
Step 5: Final expression
Thus, the moment of inertia of the system about one of the sides of H (AB) is:
Itotal=53Ml2
We have three rods:
- Rod AB (vertical)
- Rod CD (horizontal)
- Rod EF (horizontal)
Rod CD is perpendicular to rod AB. The moment of inertia I of a rod about an axis through one end and perpendicular to its length is given by the formula:
I=13ML2
For rod CD:
ICD=13Ml2
Rod EF is parallel to rod AB and is at a distance l from it. The moment of inertia I of a rod about an axis parallel to it and at a distance d is given by the parallel axis theorem:
I=Icm+Md2
where Icm is the moment of inertia about its center of mass. For rod EF:
Icm=13Ml2
The distance d from AB to EF is l:
IEF=13Ml2+M(l)2=13Ml2+Ml2=13Ml2+33Ml2=43Ml2
Now, we can find the total moment of inertia Itotal about the axis through AB:
Itotal=ICD+IEF=13Ml2+43Ml2=53Ml2
Thus, the moment of inertia of the system about one of the sides of H (AB) is:
Itotal=53Ml2
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Rotational Kinematics19videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Torque , Torque Equation And Equilibrium Of A Rigid Body29videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Displacement , Velocity And Acceleration Of Centre Of Mass30videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test30videos
THERMAL PROPERTIES OF MATTER
Similar Questions
Three identical thin rods, each of mass m and length l, are joined to form an equilateral triangular frame. Find the moment of inertia of the frame about an axis parallel to tis one side and passing through the opposite vertex. Also find its radius of gyration about the given axis.
View SolutionThree identical rods each of mass M, length l are joined to form an equilateral ΔABC . Find the Moment of Inertia about BC as shown.
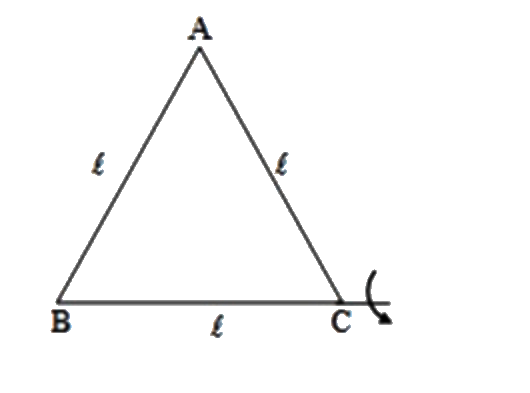 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Three identical thin rods each of length l and mass M are joined together to form a letter H. What is the moment of inertia of the system about one of the sides of H?
A16Ml2B14Ml2C23Ml2D43Ml2 - Question 2 - Select One
Three identical thin rods each of length l and mass M are joined together to from a letter H. What is the moment of inertia of the system about one of the sides of H ?
Aml24Bml23C2ml23D4ml22 - Question 3 - Select One
A rigid body is made of three identical thin rods, each of length L fastened together in the form of the letter H. The moment of inertia of this body about an axis that runs along the length of one of the legs of H is
AML23B4ML23CML2D3ML2
Two uniform, thin identical rods each of mass M and length l are joined together to form a cross. What will be the moment of inertia of the cross about an axis passing through the point at which the two rods are joined and perpendicular to the plane of the cross ?
View SolutionFour thin uniform rods each of length L and mass m are joined to form a square . The moment of inertia of square about an axis along its one diagonal is
View SolutionThree indentical thin rods each of mass m and length L are joined together to form an equilateral triangular frame . The moment of inertia of frame about an axis perpendicular to the palne of frame and apssing through a corner is
View SolutionThree thin rods each of length Land mass M are placed along x, y and z-axes such that one of each rod is at origin. The moment of inertia of this system about z-axis is
View SolutionTwo identical concentric rings each of mass m and radius R are placed perpendicularly. What is the moment of inertia of the system about the axis of one of the rings ?
View Solution

