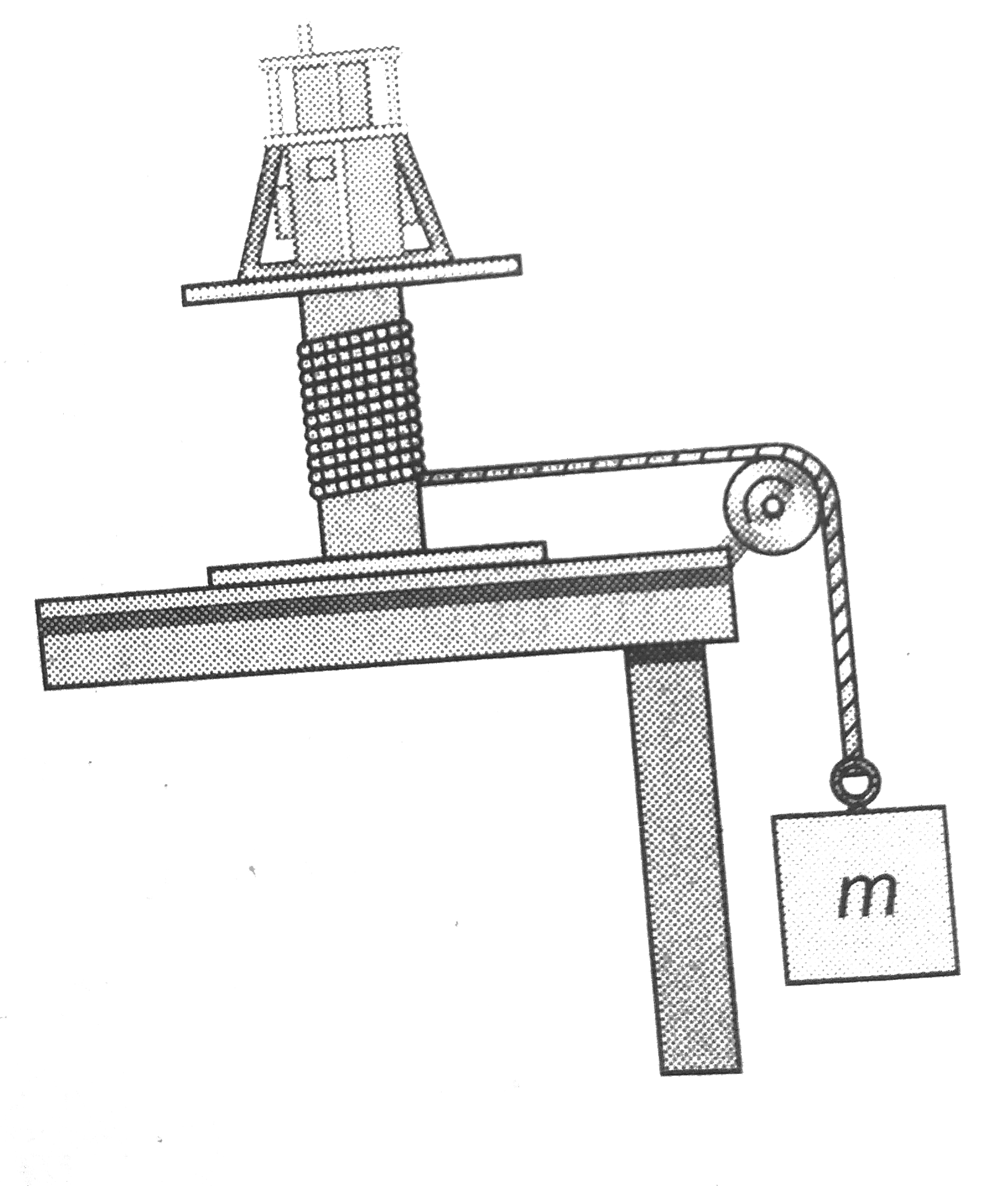
Figure shows a counterweight of mass $m$ suspended by a cord wound around a spool of radius $r$ . forming part of a turntable supporting the object. The turntable can rotate without friction. When the counterweight is released from rest, it descends through a distance $h$ , acquiring a speed $v$ . The moment of inertia $I$ of the rotating apparatus is.
.

$m r^{2} (\frac{2 g h}{v^{2}} + 1)$

$m r^{2} (\frac{g h}{v^{2}} + 1)$

$m r^{2} (\frac{2 g h}{v^{2}} - 1)$

$m r^{2} (\frac{g h}{v^{2}} + 1)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

A cord is wound around the circumference of wheel of radius r. The axis of the wheel is horizontal and $M I$ is $I$ . A weight mg is attached to the end of the cord and falls from rest. After falling through a distance h, the angular velocity of the wheel will be
A $\sqrt{\frac{2 g h}{I + m r^{2}}}$
B ${(\frac{2 m g h}{I + m r^{2}})}^{1 / 2}$
C ${(\frac{2 m g h}{I + 2 m r^{2}})}^{1 / 2}$
D $\sqrt{2 g h}$
A cord is wound round the circumference of a solid cylinder radius $R$ and mass $M$ . The axis of the cylinder is horizontal. A weight $m g$ is attached to the end of the cord and falls from rest. After falling through a distance $h$ .

A $\frac{2 m g}{M + 2 m}$
B $\sqrt{\frac{2 g h}{R^{2}}}$
C $(\frac{\sqrt{4 m g h}}{(M + 2 m) R^{2}})$
D $\sqrt{\frac{4 m g h}{M + 2 m}}$
A cord is wound round the circumference of wheel of radius $r$ . The axis of the wheel is horizontal and fixed and moment of inertia about it is $I$ . A weight $m g$ is attached to the end of the cord and falls from rest. After falling through a distance $h$ , the angular velocity of the wheel will be.
A $\sqrt{\frac{2 g h}{I + m r}}$
B $\sqrt{\frac{2 m g h}{I + m r^{2}}}$
C $\sqrt{\frac{2 m g h}{I + 2 m r^{2}}}$
D $\sqrt{2 g h}$