A body of radius R and mass m is rolling smoothly with speed v on a horizontal surface. It then rolls up a hill to a maximum height h. If h=3v2/4g. What might the body be ?
a solid circular cylinder
a hollow circular cylinder
a solid circular sphere
a hollow circular sphere.
The correct Answer is:A
(a) Interpreting h as the height increase for the centre of mass of the body, then mechanical energy conservation, Ki=Uf, leads to
12mv2com+12Iω2=mgh⇒12mv2+12I(vR)2
=mg(3v24g)
from which v cancels and we obtain I=12mR2
This moment on inertia is the moment of inertia solid cylinder.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Rotation And Translation Combined And Rolling Motion
18 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Problems Based On Mixed Concepts
31 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Angular Momentum And Its Conservation
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
Similar Questions
A ball of radius R and mass m is rolling without slipping on a horizontal surface with velocity of its centre of mass vCM. It then rolls wilthout slippig up a hill to a height h before momentarily coming to rest. Find h
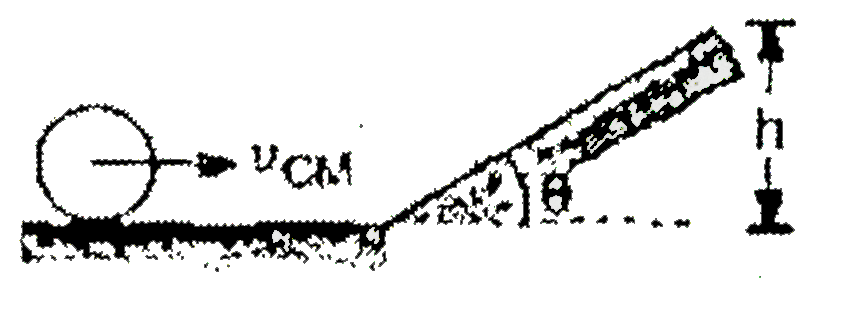
View SolutionA solid ball of radius 6.0 cm is initially rolling smoothly at 10m/s along a horizontal floor. It then rolls smoothly up a ramp until it momentarily stops. What maximum height above the floor does it reach?
View Solution
Knowledge Check
An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
Asolid sphereBhollow sphereCdiscDringA body of mass M and radius R is rolling horizontally without slipping with speed v . It then rolls up a hill to a maximum height h . If h=5v26g , what is the M.I of the body ?
AMR22B23MR2C34Mr2D25MR2An object of radius R and mass M is rolling horizontally without slipping with speed v . It then rolls up the hill to a maximum height h=3v24g . The moment of inertia of the object is ( g = acceleration due to gravity)
A25MR2BMR22CMR2D32MR2
A symmetrical body of mass M and radius R is rolling without slipping on a horizontal surface with linear speed v. Then its angular speed is
View SolutionA loop of mass M and radius R is rolling on a smooth horizontal surface with speed 'v'. It's total kinetic energy is
View SolutionA mass m of radius r is rolling horizontally without any slip with a linear speed v. It then rolls up to a height given by 34v2g
View SolutionA solid sphere of mass m and radius R rolls without slipping on a horizontal surface such that vc.m.=v0.
View SolutionA disc of radius R and mass M is rolling horizontally without slipping with speed with speed v. It then moves up an incline as shown in figure. The maximum height upto which it can reach is.
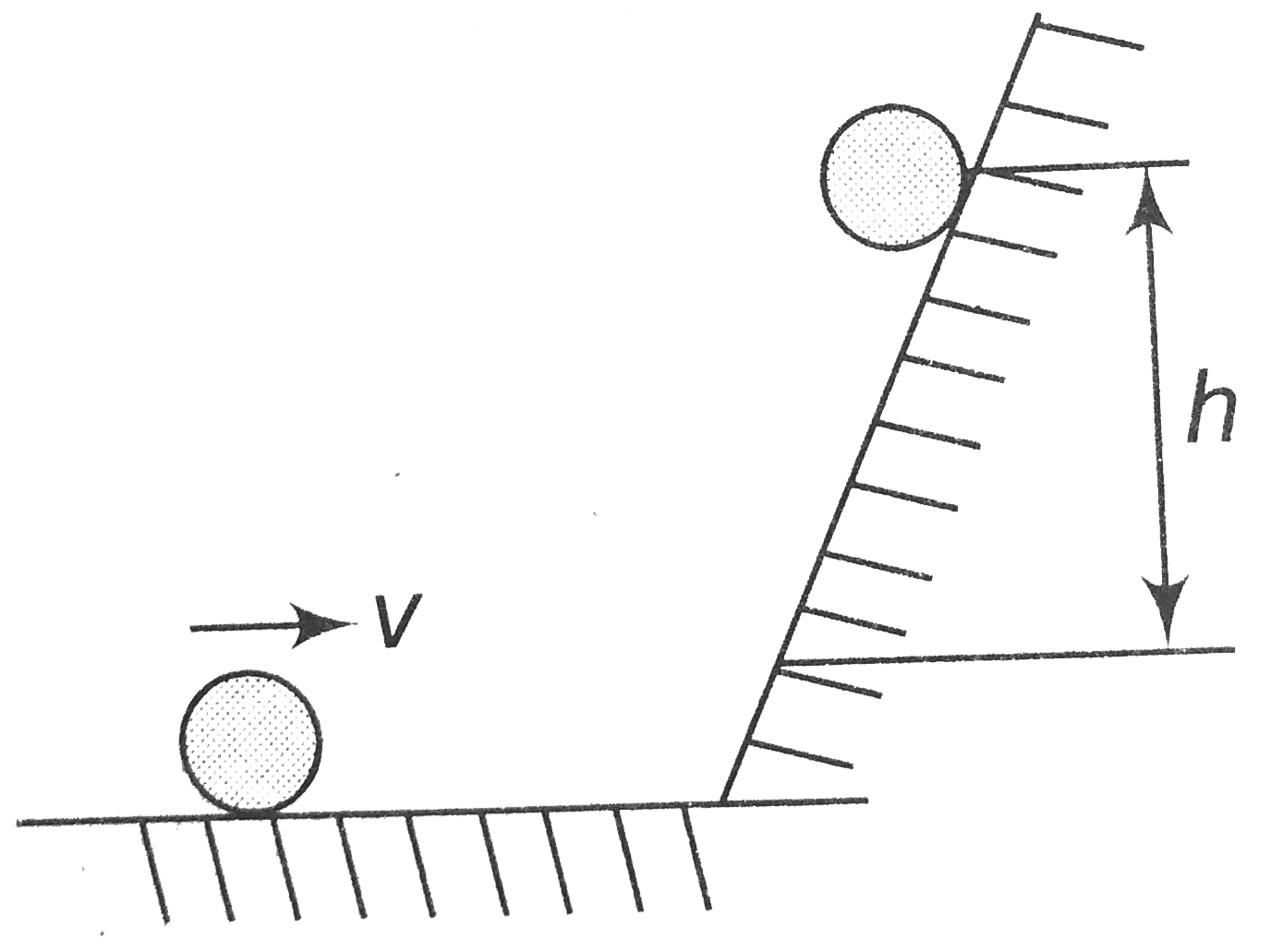 .
.
View Solution
