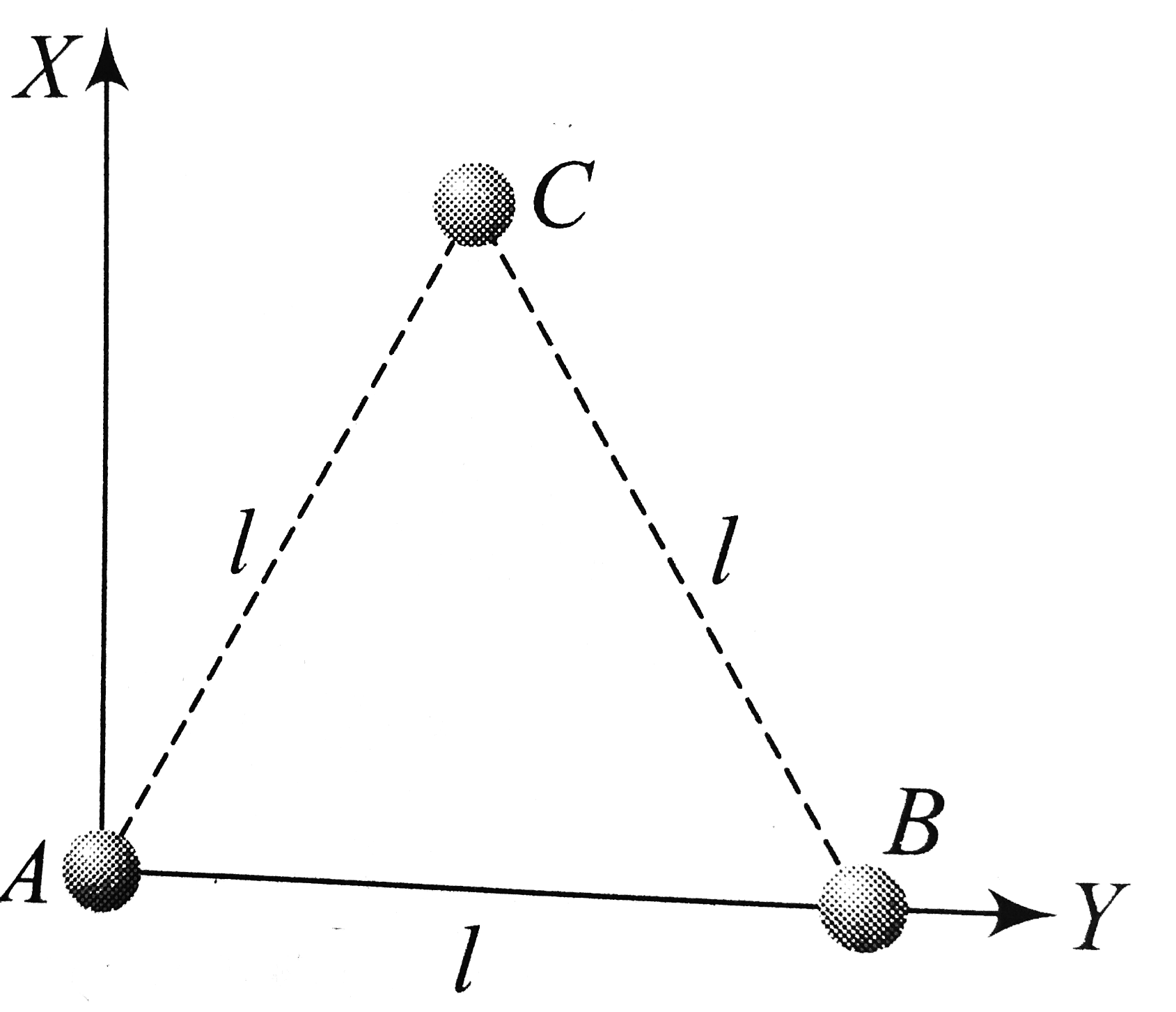
Three particles, each of mass m grams situated at the vertices of an equilateral triangle AbC of side I cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm^2 units will be.
 .
.
(3/4)ml2
2ml2
(5/4)ml2
(3/2)ml2
The correct Answer is:C
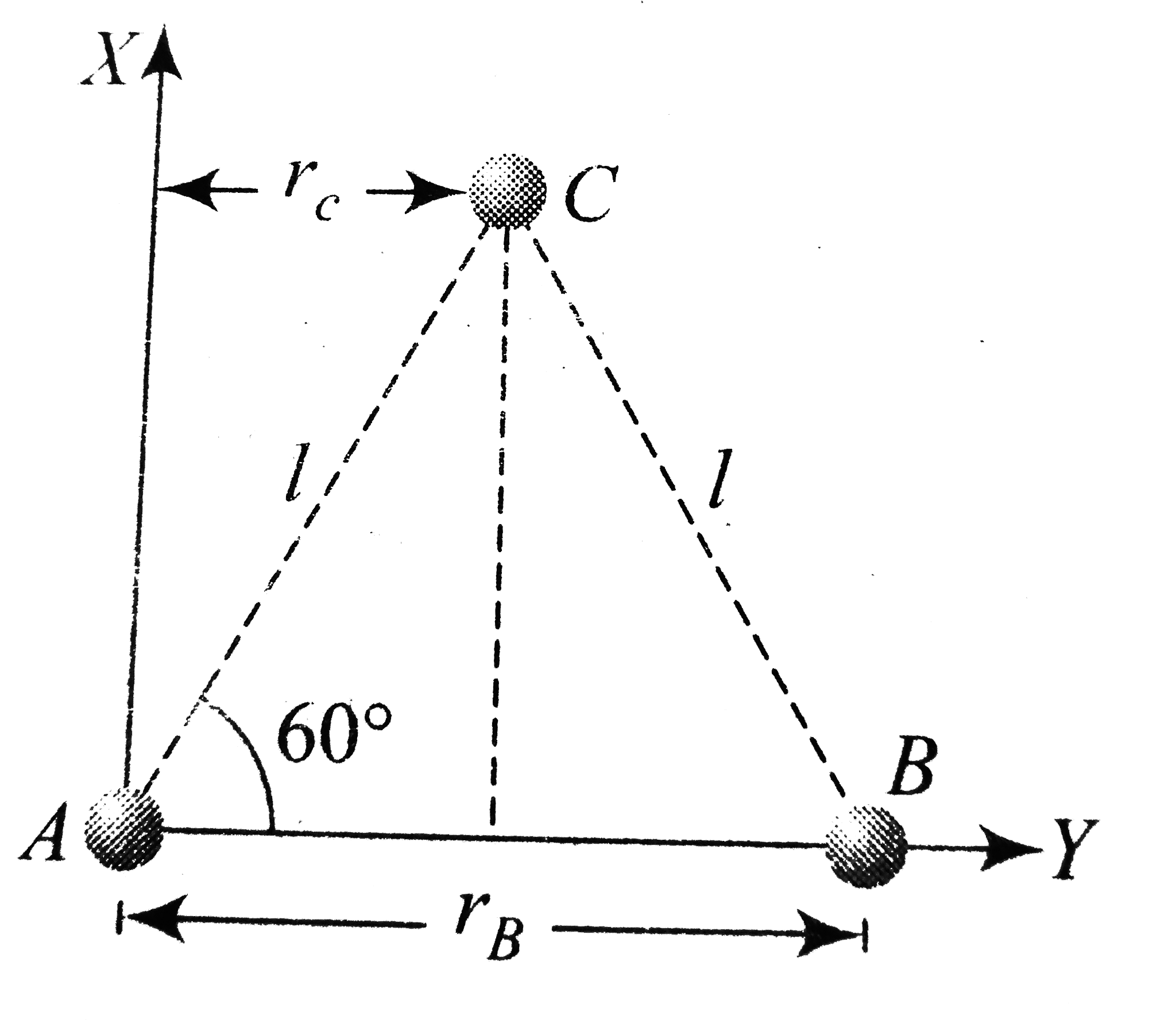
( c) Moment of inertia of the system about AX is given by
MI=mγ2AA+mBr2B+mCr2C
MI=m(0)2+m(l)2+m(lsin30∘)2
=ml2+ml24=54ml2.
 .
.
Topper's Solved these Questions
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - AIIMS Questions
40 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Assertion Reasoning
20 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
- THERMAL PROPERTIES OF MATTERBOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Chapter Test
30 Videos
Similar Questions
Three particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side l (as shown in the figure).
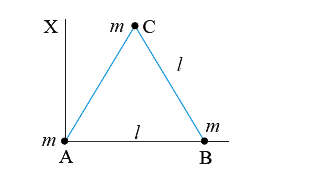
The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, will be:
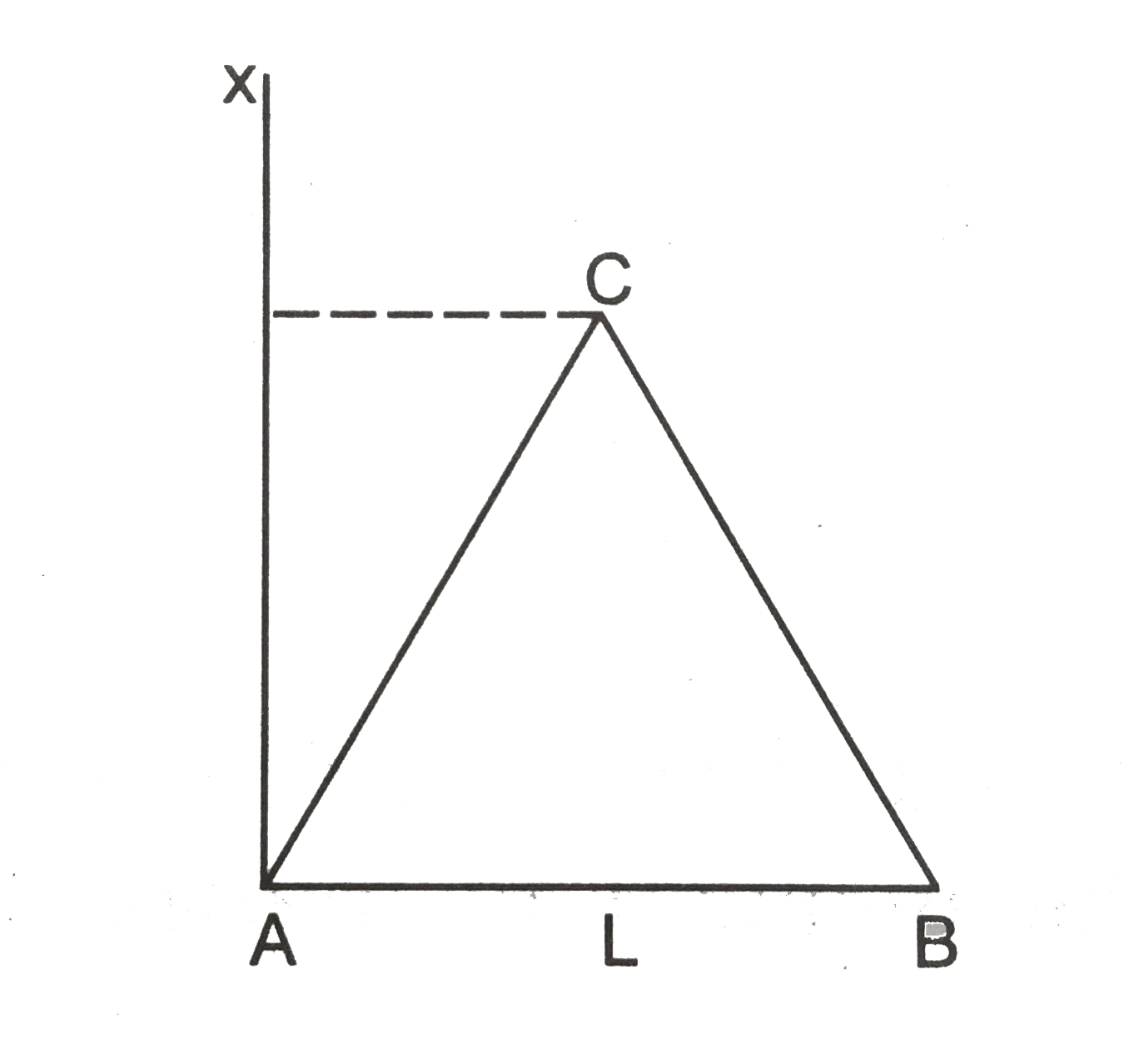
View SolutionThree particles, each of mass m are situated at the vertices of an equilateral triangle ABC of side L figure. Find thee moment of inertia of the system about the line AX perpendicular to AB in the plane of ABC
View Solution
Knowledge Check
Three particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
A2G2m2LBGm22LC3Gm22LD3Gm2LThree particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
A3ma2Bma2Cma2/3D2/3ma2Three rings each of mass M and radius R are arranged as shown in the figure. The moment of inertia of the system about YY¢ will be
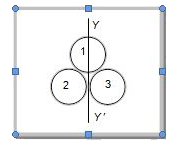 A3MR2B32MR2C5MR2D72MR2
A3MR2B32MR2C5MR2D72MR2
Three particles each of mass 12 g are located at the vertices of an equilateral triangle of side 10 cm. Calculate the moment of inertia of the system about an axis passing through the centroid and perpendicular to the plane of the triangle?
View SolutionThree particles each of mass m are kept at the vertices of an euilateral triangle of side L. The gravitational field at the centre due to these particle is
View SolutionThree point masses, each of mass m, are situated at the three corners of an equilateral triangle of each side l. The moment of inertia of this system about one of the sides of the triangle will be -
View SolutionThree masses each of mass m are placed at the vertices of an equilateral triangles ABC of side l as shown in figure. The force acting on a mass 2m placed at the centroid O of the triangle is
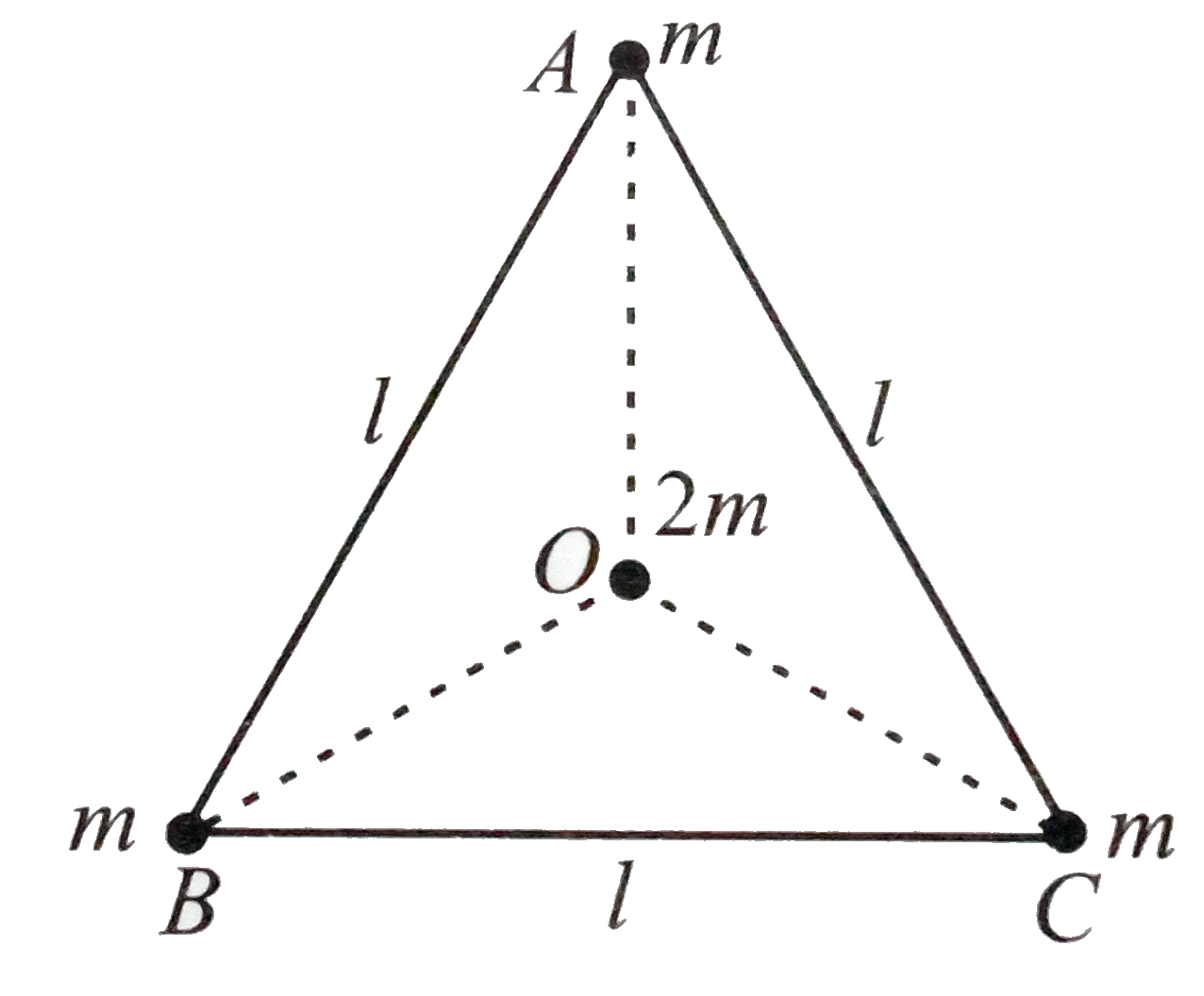
View SolutionThree point masses, each of mass m, are placed at the corner of an equilateral triangle of side 1. Then the moment of inertia of this system about an axis along one side of the triangle is
View Solution
