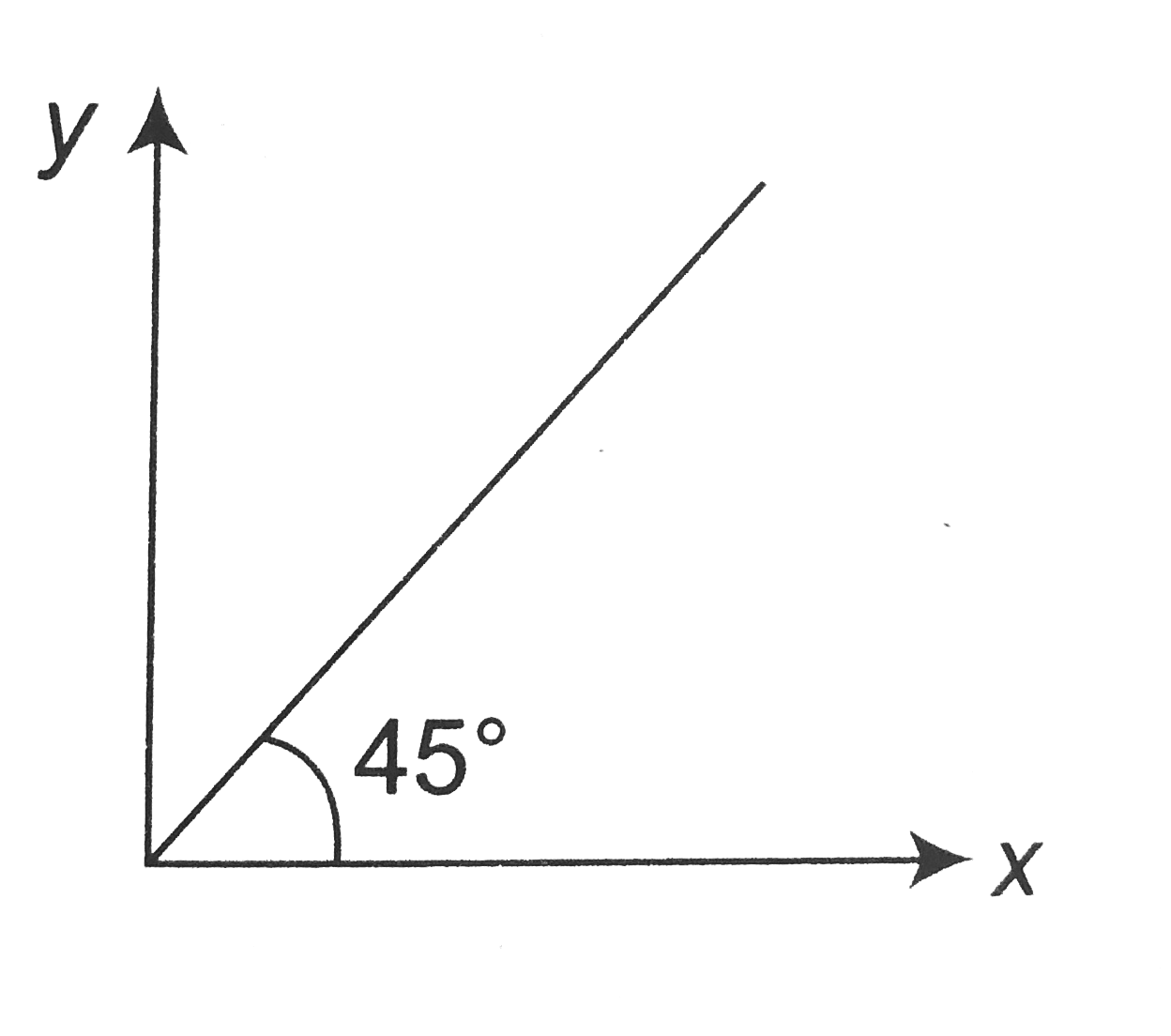
The product of Young's modulus of the material of the wire with its cross sectional area is equal to its length. Find the parameters representing x and y axes of the curve as shown:
The product of Young's modulus of the material of the wire with its cross sectional area is equal to its length. Find the parameters representing x and y axes of the curve as shown:

A

load and increase in length

B

stress and strain

C

Young's modulus and stress

D

Young's modulus and strain

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

Y=(WA)(△ll)=△l=(lYA)W
Given, YA=l Som △lW=1
also from curve its slope =tan45∘=1
So, x and y axes represent W=and△l
εW=10−1(mNm),εW=△llW
From curve, slope=tan45∘=1=lYA=△lW
So, εW=10−1=1l(△lW)=1l
l=110−1=10m=1000cm

Updated on:21/07/2023
|
Class 11PHYSICSPROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Y is the Young's modulus of the material of a wire of length L and cross-sectional area A. It is stretched through a length l. What is the force constant of the wire?

    AYA/L
    BYA/l
    CYL/A
    DYl/A

  • Young's modulus of the material of a wire is Y. ON pulling the wire by a force F, the increase in its length is x. The potential energy of the stretched wire is

    A12Fx
    B12Yx
    C12Fx2
    DNone of these

  • If Y is the Young's modulus of a wire of cross sectional area A, then the force required to increase its length by 0.1% will be

    AAY
    BAY/100
    CAY/1000
    D1000 AY