A force of is required for breaking material, If the density is then what should be the maximum length which can be hanged so that it is the point of breaking by its own weight?
The correct Answer is:A
To solve the problem step by step, we need to determine the maximum length of a material that can be suspended without breaking due to its own weight.
Step 1: Understand the Given Data
- Breaking Stress (σ): 106N/m2
- Density (ρ): 3×103kg/m3
- Acceleration due to gravity (g): 10m/s2 (approximate value)
Step 2: Relate Stress to Weight
The stress (σ) experienced by the material is given by the formula:
σ=WeightArea
The weight of the hanging material can be expressed as:
Weight=Volume×Density×g
The volume of the material can be expressed as:
Volume=Area×Length
Thus, the weight can be rewritten as:
Weight=Area×Length×ρ×g
Step 3: Substitute Weight into the Stress Formula
Substituting the expression for weight into the stress formula gives:
σ=Area×Length×ρ×gArea
This simplifies to:
σ=Length×ρ×g
Step 4: Solve for Length
Now, we can set the stress equal to the breaking stress:
106=Length×(3×103)×10
This simplifies to:
106=Length×3×104
Now, solve for Length:
Length=1063×104
Length=1063×104=1023=1003≈33.33m
Step 5: Conclusion
The maximum length of the material that can be hanged without breaking due to its own weight is approximately:
Length≈33.33m
- Breaking Stress (σ): 106N/m2
- Density (ρ): 3×103kg/m3
- Acceleration due to gravity (g): 10m/s2 (approximate value)
The stress (σ) experienced by the material is given by the formula:
σ=WeightArea
The weight of the hanging material can be expressed as:
Weight=Volume×Density×g
The volume of the material can be expressed as:
Volume=Area×Length
Thus, the weight can be rewritten as:
Weight=Area×Length×ρ×g
Substituting the expression for weight into the stress formula gives:
σ=Area×Length×ρ×gArea
This simplifies to:
σ=Length×ρ×g
Now, we can set the stress equal to the breaking stress:
106=Length×(3×103)×10
This simplifies to:
106=Length×3×104
Now, solve for Length:
Length=1063×104
Length=1063×104=1023=1003≈33.33m
The maximum length of the material that can be hanged without breaking due to its own weight is approximately:
Length≈33.33m
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Surface Tension And Surface Energy
29 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Pressure Difference And Capillarity
23 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Bulk Modulus And Shear Modulus
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- ROTATIONAL DYNAMICSBOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test
29 Videos
Similar Questions
Breaking stress for a material is 2×108N/m2. What maximum length of the wire of this material can be taken t the wire does not break by own weight? Density of material = 5×103kg/m3
View SolutionFor steel the breaking stressis 6×106N/m2 and the density is 8×103kg/m3. The maximum length of steel wire, which can be suspended witout breaking under its own weight is [g=10m/s2]
View Solution
Knowledge Check
A stress of 106N/m2 is required for breaking a material. If the density of the material is 3×103Kg/m3, then what should be the minimum length of the wire made of the same material so that it breaks by its own weight (g=10m/s2)
A33.4mB3.4mC34cmD3.4cmA stress of 106Nm−2 is required for breaking a material. If the density of the material is 3×103kgm−3., then what should be the length of the wire made of this material, so that it breakes under its own weight?
A10 mB33.3 mC5 mD66.6 mA force of 6×106Nm−2 required for breaking a material. The denisty ρ of the material is 3×103kgm−3. If the wire is to break under its own weight, then the length of the wire made of that material should be (Given, g = 10 ms−2)
A20 mB200 mC100 mD2000 m
A substance breaks down by a stress of 106N/m2. If the density of the material of the wire is 3×103kg/m3, then the length of the wire of that substance which will break under its own weight, when suspended vertically, is its own weight, when suspended vertically, is
View SolutionA substance breaks down by a stress of 106Nm−2. If the density of the material of the wire is 3×103kgm−3. Then the length of the wire of the substance which will break under its own weight when suspended vertically is
View SolutionA substance breaks down under a stress of 105 Pa. If the density of the substance is 2×103kg/m3, find the minimum length of the wire made of this substance which will break under its own weight (g=10m/s).
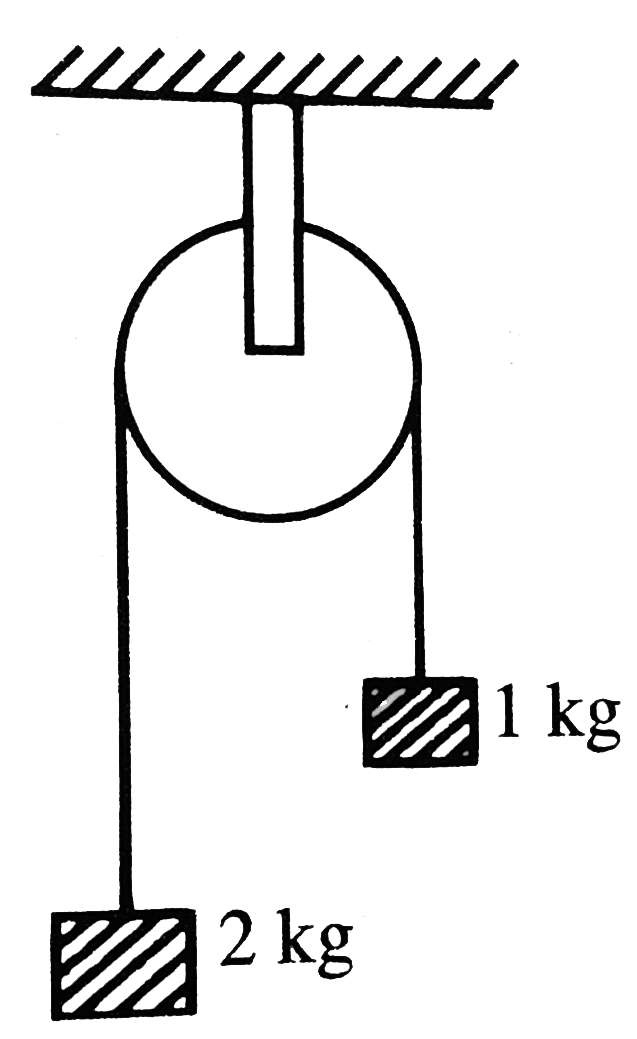
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire goijng over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−12, then what should be the minimum radlus of the wire used if it is not to break?
View SolutionA man slides down a light rope whose breaking strength in η times his weight (η<1). What should be his maximum acceleration so that the rope just breaks ?
View Solution
