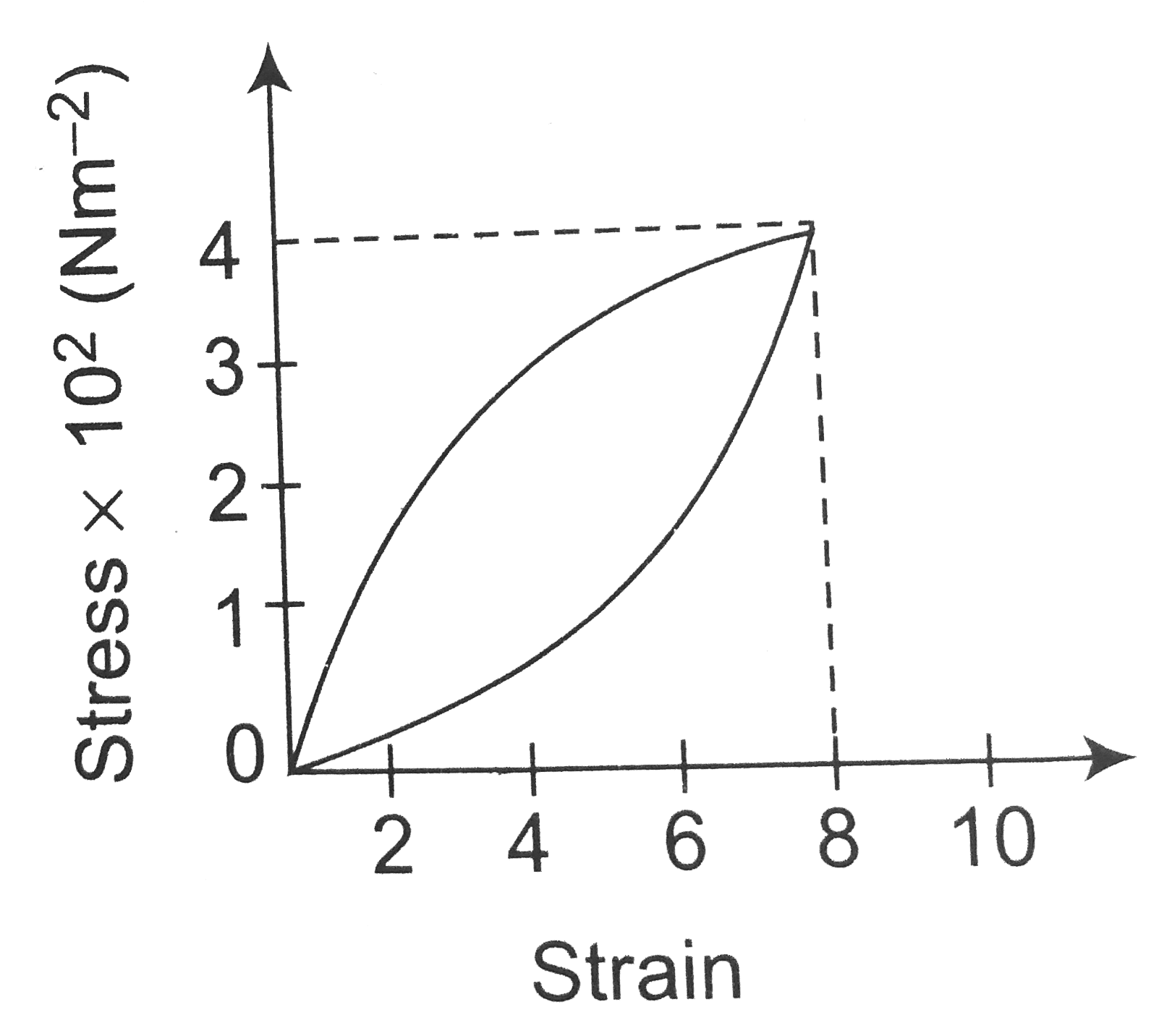
A rubber of volume 2000 cc is alternately subjected to tension and released. The figure shown the stress-strain curve of rubber. Each curve is a quadrant of an ellipse. The amount of energy lost as heat per cycle per unit volume will be
(π2−1)×16×102J
(π4−1)×8×102J
(π4−1)×32×102J
(π2−1)×32×102J
The correct Answer is:D
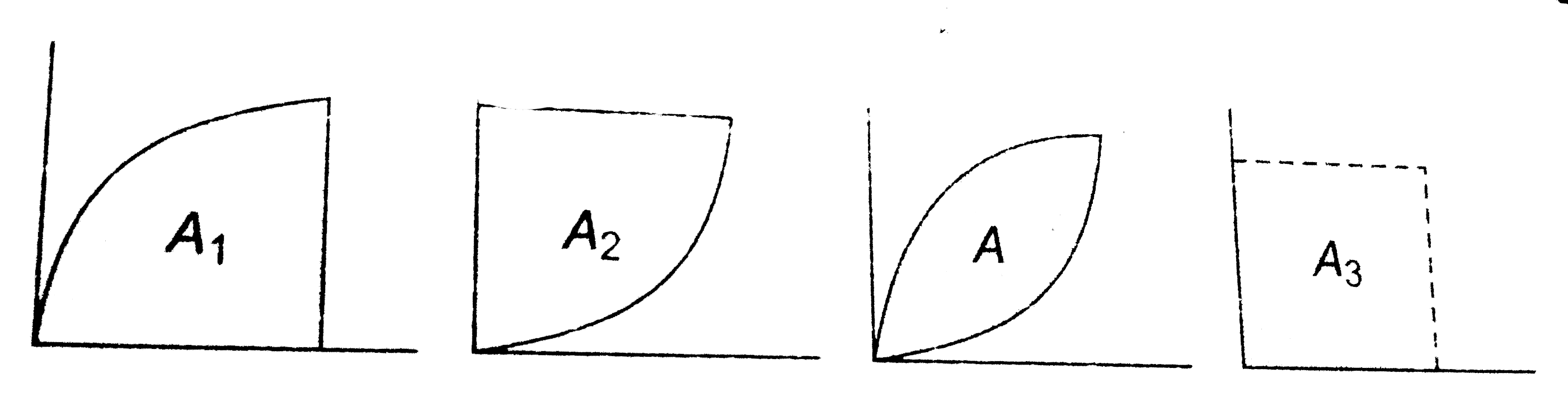
Hysteresis loss corresponding to elasticity per unit volume of a substance is given by the area of hysteresis loop, i.e., stress-strain curve corresponding to one complete loading and deloading
Area of an ellipse=π×semi-major axis×semi-minor axis
A1=14(π×8×4×102) and A2=14(π×8×4×102)
Also, A3=8×4×102
Area of hysteresis loop is A=A1+A2+A3
A=2[π4×8×4×102]−[8×4×102]
=work done per cycle
=energy lost per cycle per unit volume.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Surface Tension And Surface Energy29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Pressure Difference And Capillarity23videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Bulk Modulus And Shear Modulus29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
Knowledge Check
- Question 1 - Select One

The stress strain curves for brass, steel and rubber are shown in the figure. The lines A, B and C are forARubber, brass and steel respectivelyBBrass, steel and rubber respectivelyCSteel, brass and rubber respectivelyDSteel, rubber and brass respectively - Question 2 - Select One
If a number of little droplets of water, each of radius r, coalesce to form a single drop of radius R, show that the rise in temperature will be given by 3TJ(1r−1R) where T is the surface tension of water and J is the mechanical equivalent of heat.
A2TJ(1r−1R)B2TrJC3TrJD3TJ(1r−1R) - Question 3 - Select One
When a force is applied at one end of an elastic wire, it produce a strain E in the wire. If Y is the Young's modulus of the material of the wire, the amount of energy stored per unit volume of the wire is given by
AY×EB12(Y×E)CY×E2D12(Y×E2)
If 20kJ work is done by the water fall per unit volume of water and 30kJ heat was lost per unit volume, the energy change per unit volume of water is:
View SolutionLe chatelier's principle
If a system at equilibrium is subjected to a change of any one of the factors such as concentration, pressure or temperature, the system adjusts itself in such a way so as to minimise the effect of that change. Change of pressure: If a system in equilibrium consists of gases, then the concentrations of all the components can be altered by changing the pressure.When the pressure on the system is increased, the volume decreases proportionately.The total number of moles per unit volume will now be more and the equilibrium will shift in the direction in which there is decrease in number of moles i.e., towards the direction in which there is decrease in volume.
Effect of pressure on melting point : There are two types of solids :
(a)Solids whose volume decreases on melting e.g. ice, diamond , carborundum, magnesium nitride and quartz.
Solid (higher volume)⇔ Liquid (lower volume)
The process of melting is facilitated at high pressure, thus melting point is lowered.
(b)Solids whose volume increase on melting, e.g. Fe,Cu, Ag,Au, etc.
Solid (lower volume)⇔ Liquid (higher volume)
In this case the process of melting becomes difficult at high pressure, then melting point becomes high.
(c )Solubility of subtances : When solid substance are dissolved in water, either heat is evolved (exothermic) or heat is absorbed (endothermic).
KCl+aq⇔KCl(aq)-heat
In such cases,solubility increase with increase in temperature.
Consider the case of KOH, when this is dissolved heat is evolved.
KOH+aq⇔KOH(aq)+heat
In such cases, solubility decrease with increase in temperature.
(d)Solubility of gases in liquids : When a gas dissolves in liquid, there is decreases in volume. Thus, increases of pressure will favour the dissolution of gas in liquid.
Effect of temperature: Le-Chatelier's principle predicts a system at equilibrium will tend to shift in the endothermic direction when temperature is raised, for then energy is absorbed as heat and the rise in temperature is opposed.Conversely, an equilibrium will shift in the exothermic direction if the temperature is lowered, for then energy is released and the reduction in temperture is opposed Van't Hoff equation shows the dependence of equilibrium constant K on temperaure as :
ddTlnK=ΔH∘RT2orlnK=constant−ΔH∘R.1T
Au(s)⇔Au(l)View SolutionLe chatelier's principle
If a system at equilibrium is subjected to a change of any one of the factors such as concentration, pressure or temperature, the system adjusts itself in such a way so as to minimise the effect of that change. Change of pressure: If a system in equilibrium consists of gases, then the concentrations of all the components can be altered by changing the pressure.When the pressure on the system is increased, the volume decreases proportionately.The total number of moles per unit volume will now be more and the equilibrium will shift in the direction in which there is decrease in number of moles i.e., towards the direction in which there is decrease in volume.
Effect of pressure on melting point : There are two types of solids :
(a)Solids whose volume decreases on melting e.g. ice, diamond , carborundum, magnesium nitride and quartz.
Solid (higher volume)⇔ Liquid (lower volume)
The process of melting is facilitated at high pressure, thus melting point is lowered.
(b)Solids whose volume increase on melting, e.g. Fe,Cu, Ag,Au, etc.
Solid (lower volume)⇔ Liquid (higher volume)
In this case the process of melting becomes difficult at high pressure, then melting point becomes high.
(c )Solubility of subtances : When solid substance are dissolved in water, either heat is evolved (exothermic) or heat is absorbed (endothermic).
KCl+aq⇔KCl(aq)-heat
In such cases,solubility increase with increase in temperature.
Consider the case of KOH, when this is dissolved heat is evolved.
KOH+aq⇔KOH(aq)+heat
In such cases, solubility decrease with increase in temperature.
(d)Solubility of gases in liquids : When a gas dissolves in liquid, there is decreases in volume. Thus, increases of pressure will favour the dissolution of gas in liquid.
Effect of temperature: Le-Chatelier's principle predicts a system at equilibrium will tend to shift in the endothermic direction when temperature is raised, for then energy is absorbed as heat and the rise in temperature is opposed.Conversely, an equilibrium will shift in the exothermic direction if the temperature is lowered, for then energy is released and the reduction in temperture is opposed Van't Hoff equation shows the dependence of equilibrium constant K on temperaure as :
ddTlnK=ΔH∘RT2orlnK=constant−ΔH∘R.1T
The plot of log K against 1T is a straight line with positive slope ( K being the equilibrium constant of a reaction ), which of the following is then correct ?View SolutionLe chatelier's principle
If a system at equilibrium is subjected to a change of any one of the factors such as concentration, pressure or temperature, the system adjusts itself in such a way so as to minimise the effect of that change. Change of pressure: If a system in equilibrium consists of gases, then the concentrations of all the components can be altered by changing the pressure.When the pressure on the system is increased, the volume decreases proportionately.The total number of moles per unit volume will now be more and the equilibrium will shift in the direction in which there is decrease in number of moles i.e., towards the direction in which there is decrease in volume.
Effect of pressure on melting point : There are two types of solids :
(a)Solids whose volume decreases on melting e.g. ice, diamond , carborundum, magnesium nitride and quartz.
Solid (higher volume)⇔ Liquid (lower volume)
The process of melting is facilitated at high pressure, thus melting point is lowered.
(b)Solids whose volume increase on melting, e.g. Fe,Cu, Ag,Au, etc.
Solid (lower volume)⇔ Liquid (higher volume)
In this case the process of melting becomes difficult at high pressure, then melting point becomes high.
(c )Solubility of subtances : When solid substance are dissolved in water, either heat is evolved (exothermic) or heat is absorbed (endothermic).
KCl+aq⇔KCl(aq)-heat
In such cases,solubility increase with increase in temperature.
Consider the case of KOH, when this is dissolved heat is evolved.
KOH+aq⇔KOH(aq)+heat
In such cases, solubility decrease with increase in temperature.
(d)Solubility of gases in liquids : When a gas dissolves in liquid, there is decreases in volume. Thus, increases of pressure will favour the dissolution of gas in liquid.
Effect of temperature: Le-Chatelier's principle predicts a system at equilibrium will tend to shift in the endothermic direction when temperature is raised, for then energy is absorbed as heat and the rise in temperature is opposed.Conversely, an equilibrium will shift in the exothermic direction if the temperature is lowered, for then energy is released and the reduction in temperture is opposed Van't Hoff equation shows the dependence of equilibrium constant K on temperaure as :
ddTlnK=ΔH∘RT2orlnK=constant−ΔH∘R.1T
For the reaction 12N2(g)+12O2(g)⇔NO(g)View SolutionThe stored energy per unit volume of a stretched wire is
View Solution

