If layer thickness L2 is 1.4cm, then its thermal conductivity K2 will have value (in W/mK)
2×10−2
2×10−3
4×10−2
4×10−3
The correct Answer is:A
ΔQΔT∣∣∣layer2 = ΔQΔT∣∣∣layer4
⇒0.06×A×51.5×10−2=K2×A×141.4×10(−2)
⇒K2=0.02W/mK.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Transmission Of Heat : Radiation28videos
THERMAL PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Problems Baesd On Mixed Concepts18videos
THERMAL PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Calorimetry41videos
THERMAL PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
- BOOK - A2ZCHAPTER - UNIT, DIMENSION AND ERROR ANALYSISEXERCISE - Chapter Test28videos
UNIT, DIMENSION AND ERROR ANALYSIS
Similar Questions
Show that the SI units of thermal conductivity are W/m−K.
View SolutionTwo plates each of area A thickness L1 and L2 thermal conductivities K1 and K2 respectively are joined to from a single plate of thickness (L1+L2) If the temperatures of the free surfaces are θ1 and θ2 Calculate
(a) Rate of flow of heat
(b) Temperature of interface
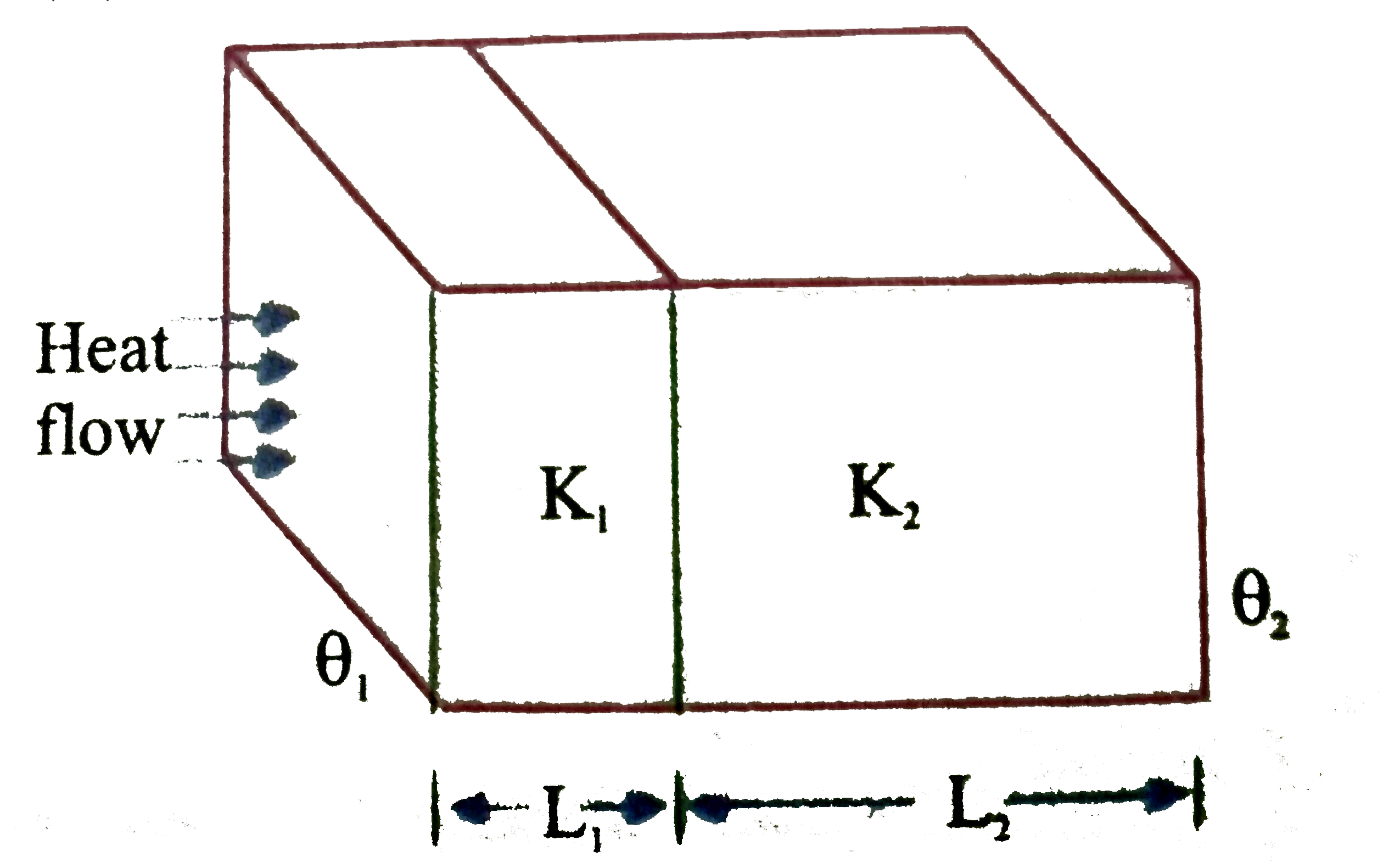 .View Solution
.View Solution
Knowledge Check
- Question 1 - Select One
Assertion : The equivalent thermal conductivity of two plates of same thickness in contact (series) is less than the smaller value of thermal conductivity.
Reason : For two plates of equal thickness in contact (series) the equivalent thermal conductivity is given by
1K=1K1+1K2AIf both the assertion and reason are true and reason is the correct explanation of the assertion.BIf both the assertion and reason are true but the reason is not correct explanation of the assertion.CIf the assertion is true but the reason is falseDIf the both the assertion and reason are false. - Question 2 - Select One
A wall has two layers A and B each made of different materials. The layer A is 10cm thick and B is 20 cm thick. The thermal conductivity of A is thrice that of B. Under thermal equilibrium temperature difference across the wall is 35∘C. The difference of temperature across the layer A is
A30∘CB14∘CC8.75∘CD5∘C - Question 3 - Select One
A slab consists of two parallel layers of two different materials of same thickness having thermal conductivities K1andK2. The equivalent conductivity of the combination is
AK1+K2BK1+K22C2K1K2K1+K2DK1+K22K1K2
A composite slab is prepared by pasting two plates of thickness L1 and L2 and thermal conductivites K1 and K2 . The slab have equal cross-sectional area. Find the equivalent conductivity of the composite slab.
View SolutionTwo plates eachb of area A, thickness L1andL2 thermal conductivities K1andK2 respectively are joined to form a single plate of thickness (L1+L2). If the temperatures of the free surfaces are T1andT2. Calculate.

(a) rate of flow of heat
(b) temperature of interface and
(c) equivalent thermal conductivity.View SolutionFigure shows the cross section of a wall made of three layers. The layer thicknesses are L1,L2=0.750L1, and L3=0.350L1. The thermal conductivities are k1,k2=0.900k1, and k3=0.800k1. The temperature at the left side and right side of the wall are TH=30.0∘C and TC=−15.0∘C, respectively. Thermal conduction is steady . (a) What is the temperature difference ΔT2 across layer 2 ( between the left and right sides of the layer ) ? If k2 were, instead, equal to 1.1k1, (b) would the reate at which energy is conducted through the wall be greater than, less than, or the same as proviously, and (c ) what would be the value of ΔT2 ?
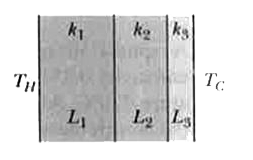 View Solution
View SolutionDefine coefficient of thermal conductivity. Two metal slabs of same area of cross-section, thickness d1 and d2 having thermal conductivities K1 and K2 respectively are kept in contact. Deduce expression for equivalent thermal conductivity.
View SolutionA wall consists of two layer, one of thickness 3 cm and other of 6 cm. the thermal conductivities of the materials of these layers are K and 3K respectively. The temperature of the outer surfaces of the two layers are −5∘C and 20∘C respectively. determine the temperature of the surface of contact of the two layers in the steady state.
View Solution

