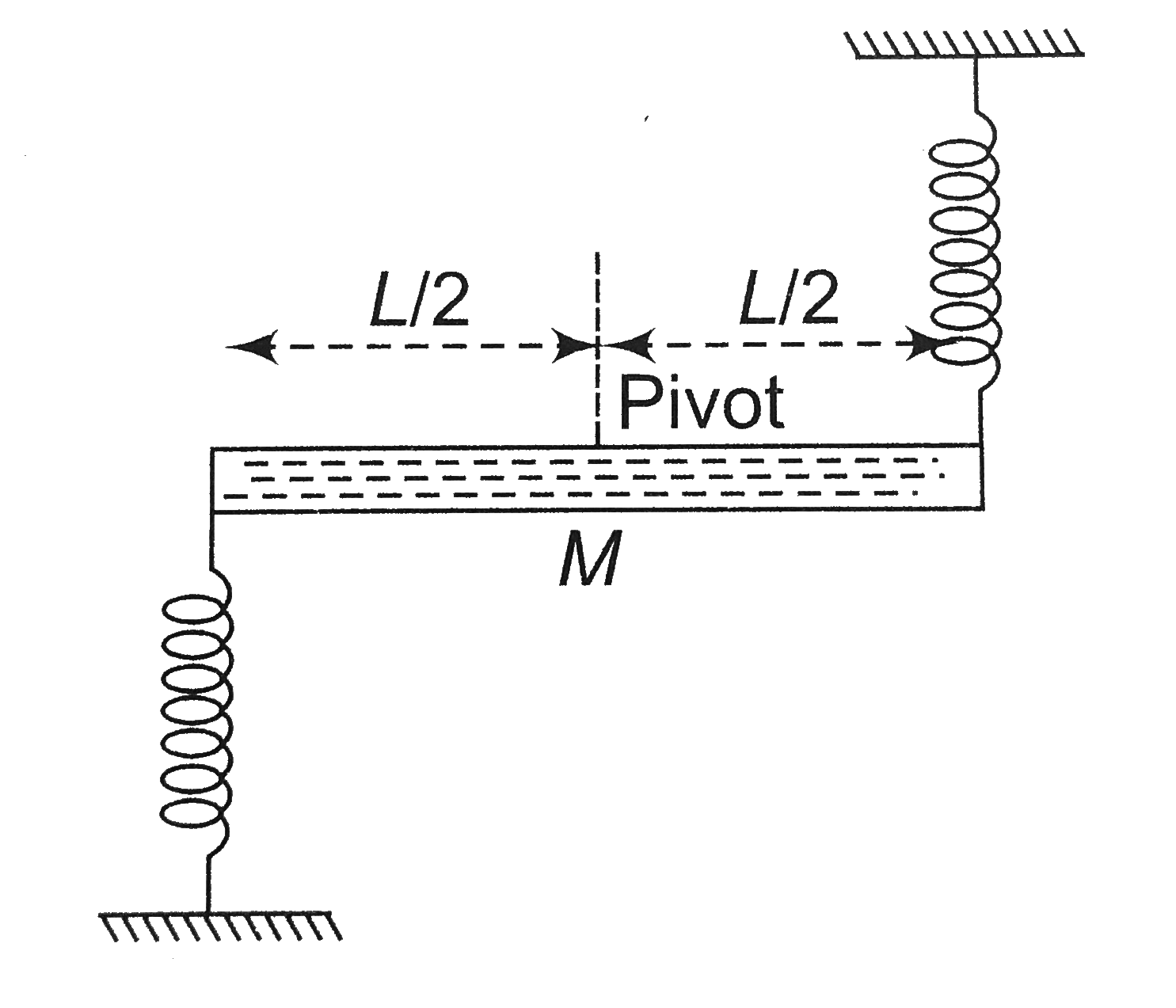
A uniform stick of mass M and length L is pivoted its come its ands are fast to two spring each of the constant K. In the position shown in figure the same through a small length when spring is display through a small angle of and released. The stick :
executes non- periodic motion
executes periodic motion which in its not simple harmonic
executesS.H.M. of frequency 12π√6KM
executesS.H.M. of frequency 12π√K2M
The correct Answer is:C
if stick is rotated through x small angle θthe spring as streached by a distance L2g Therefore resulting force is spring =K(k2g) each spring causes a temper τ(=Fd)=(kLθ2)L2 an the same direction Therefore equation of rotation motion is
τ=1a
−2(KLθ2)k2=1awith1=ML212
a=−(68M)gg
syanderd equation of angle S.H.M is a=−ω2θ
ω2=6kM
equencyf=ω2π=12π√6kM
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning22videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - NEET Questions39videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Superposition Of Shm And Compound Pendulum19videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test30videos
NEWTONS LAWS OF MOTION
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test29videos
PROPERTIES OF MATTER
Similar Questions
two light identical springs of spring constant K are attached horizontally at the two ends of a uniform horizontal rod AB of length l and mass m. the rod is pivoted at its centre 'o' and can rotate freely in horizontal plane . The other ends of the two springs are fixed to rigid supportss as shown in figure . the rod is gently pushed through a small angle and released , the frequency of resulting oscillation is :
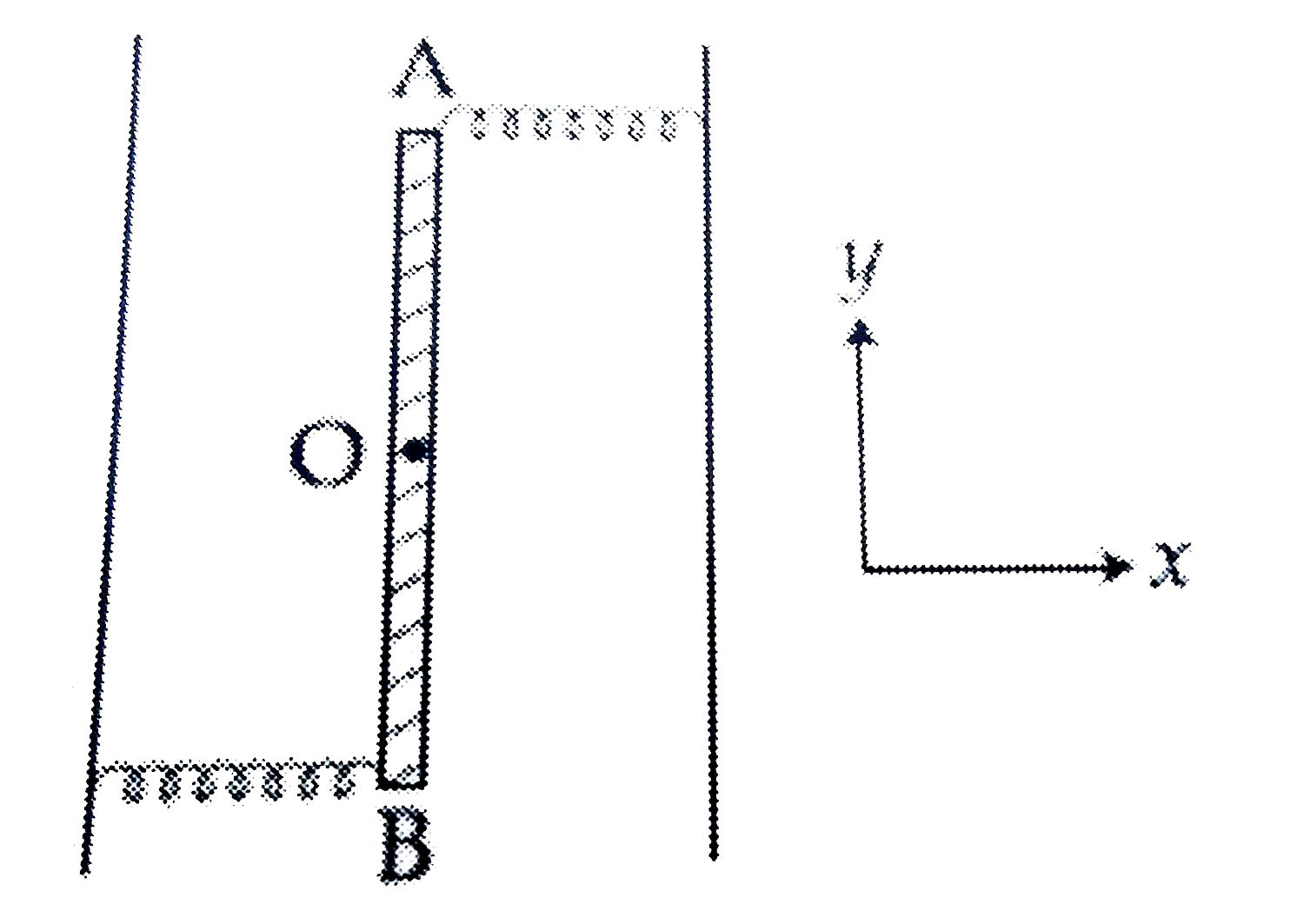 View Solution
View Solution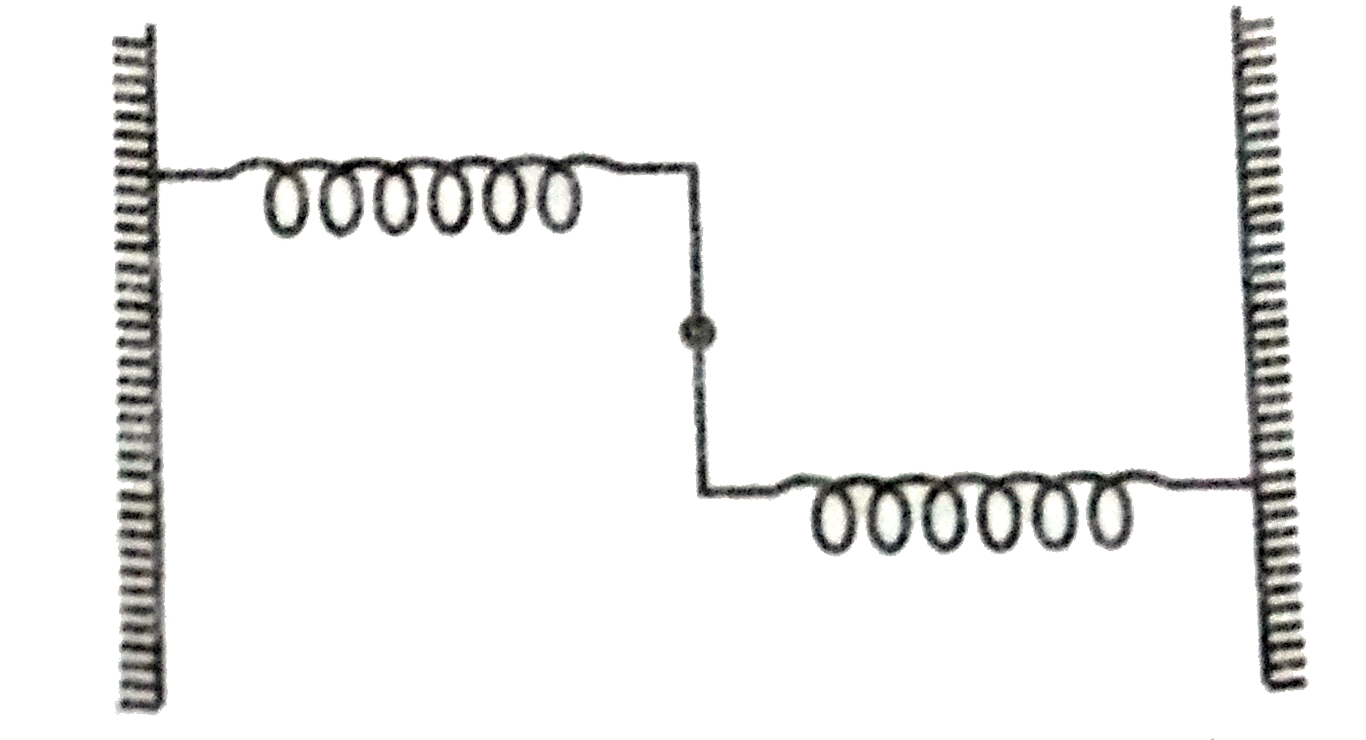
A uniform rod of length l and mass M is pivoted at the centre. Its two ends are attached to two ends are attached to two springs of equal spring constant k. the springs are fixed to rigid support as shown in figure and the rod is free to oscillate in the horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscillation isView Solution
Knowledge Check
- Question 1 - Select One
A stick of mass m and length l is pivoted at one end and is displaced through an angle θ. The increase in potential energy is
 Amg(l)2(1−cosθ)Bmg(l)2(1+cosθ)Cmg(l)2(1−sinθ)Dmg(l)2(1+sinθ)
Amg(l)2(1−cosθ)Bmg(l)2(1+cosθ)Cmg(l)2(1−sinθ)Dmg(l)2(1+sinθ) - Question 2 - Select One
A uniform rod of length L and mass M is pivotedat the centre. Its two ends are attached to two springs of equal spring constants. k. The springs as shown in the figure, and the rod is free to oscillate in hte horizontal plane. the rod is gently pushed through a small angle θ in one direction and released. the frequency of oscilllation is-
 A12π√2kMB12π√kMC12π√6kMD12π√24kM
A12π√2kMB12π√kMC12π√6kMD12π√24kM - Question 3 - Select One

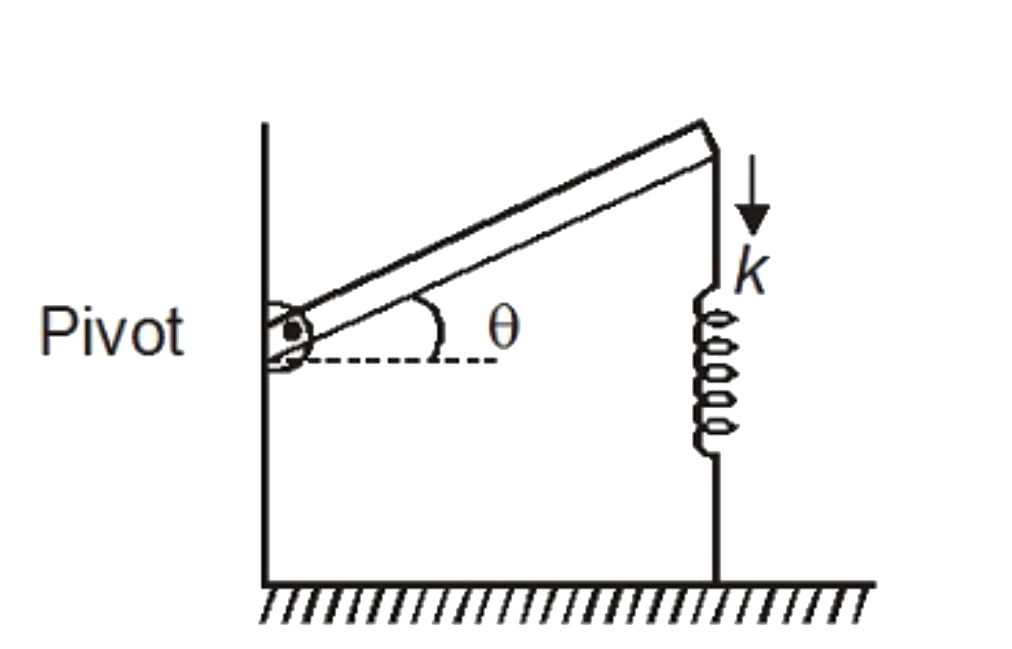
A horizontal rod of mass m and length L is pivoted at one end The rod's other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released. The angular frequency of the subsequent simple harmonic motion isA√3kmB√k3mC√3km+3g2LD√km
A horizontal rod of mass m=3kπ2 kg and length L is pivoted at one end . The rod at the other end is supported by a spring of force constant k. The rod is displaced by a small angle θ from its horizontal equilibrium position and released . The time period (in second) of the subsequent simple harmonic motion is
 View Solution
View SolutionA uniform rod of mass 2m and length L is hinged at one end and carries a particle of mass m at the other end.Two springs each of force constant k are installed at distances as shown.The whole arrangement rests on a smooth horizontal surface.The frequency of small oscillations will be?
View Solution
A thin uniform vertical rod of mass m and length l pivoted at point O is shown is Fig. The combined stiffness of the springs is equal to k. The mass of the spring is negligible. The frequency of small oscillation is .View SolutionA thin uniform vertical rod of mass m and length l pivoted at point O is shown in Fig. The combined stiffness of the springs is equal to k. The mass of the springs is negligible. The angular frequency of small oscillation is
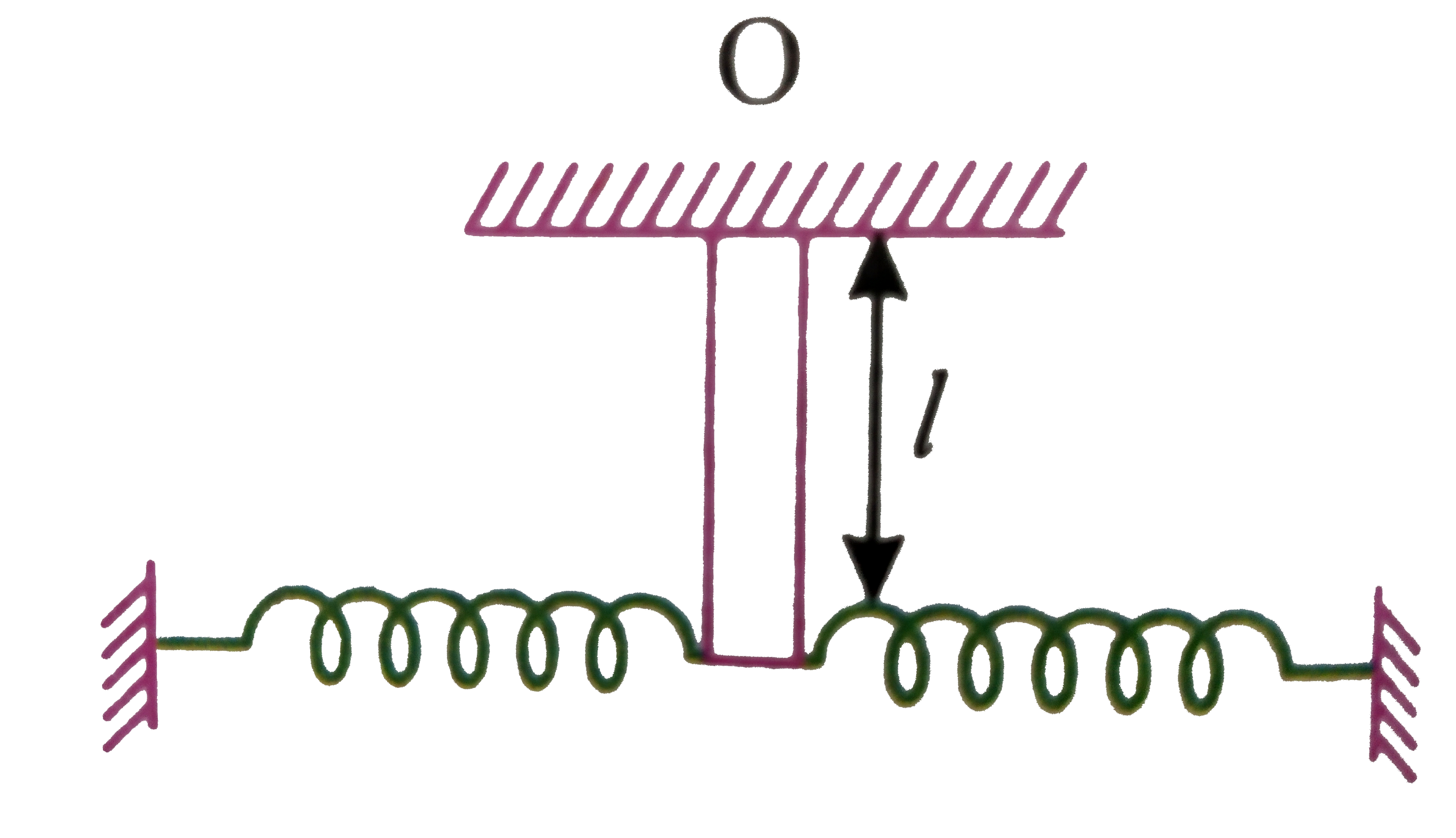 View Solution
View SolutionA uniform disc of mass m is attached to a spring of spring constant k as shown in figure and there is sufficient friction to prevent slipping of disc. Time period of small oscillations of disc is:
 View Solution
View Solution

