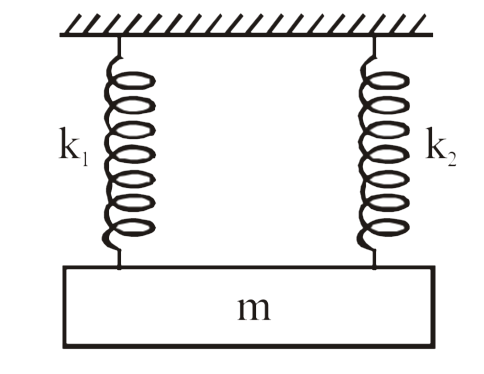
A mass m is suspended separately by two different springs of spring constant k1 and k2 given the time period t1 and t2 respectively. If the same mass m is shown in the figure then time period t is given by the relation

t=t1+t2
t=t1t2t1+t2
t2=t21+t22
t−2=t−21+t−22
The correct Answer is:D
t1=2π√mk1 and t2=2π√mk2
Equivalant constant for shown combination is , (K1+K2 so time period t is given by
t=2π√mK1+K2
By solving these equations we get T2=t21+t22
Topper's Solved these Questions
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - AIIMS Questions
24 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test
29 Videos
- OSCILLATION AND SIMPLE HARMONIC MOTIONBOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Assertion Reasoning
22 Videos
- NEWTONS LAWS OF MOTIONBOOK - A2ZCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Chapter Test
30 Videos
- PROPERTIES OF MATTERBOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Chapter Test
29 Videos
Similar Questions
A mass is suspended separately by two different springs in successive order, then time periods is t1andt2 respectively. It is connected by both springs as shown in fig. then time period is t0. The correct relation is
View SolutionTwo spring of spring constants k1 and k2 ar joined and are connected to a mass m as shown in the figure. Calculate the frequency of oscillation of mass m.

View Solution
Knowledge Check
A mass is suspended separately by two different springs in successive order then time periods is t1 and t2 respectively. If it is connected by both spring as shown in figure then time period is to, the correct relation is
 At20=t21+t22Bt−20=t−21+t−22Ct−10=t−11+t−12Dt0=t1+t2
At20=t21+t22Bt−20=t−21+t−22Ct−10=t−11+t−12Dt0=t1+t2A mass is suspended separately by two springs of spring constants k1 and k2 in successive order. The time periods of oscillations in the two cases are T1 and T2 respectively. If the same mass be suspended by connecting the two springs in parallel, (as shown in figure) then the time period of oscillations is T. The correct relations is
 AT2=T21+T22BT−2=T−21+T−22CT−1=T−11+T−12DT=T1+T2
AT2=T21+T22BT−2=T−21+T−22CT−1=T−11+T−12DT=T1+T2When a block of mass m is suspended separately by two different springs have time period t1 and t2. If same mass is connected to parallel combination of both springs, then its time period is given by :-
At1t2t1+t2Bt1t2√t21+t22C√t1t2t1+t2Dt1+t2
A mass m is suspended from the two coupled springs connected in series. The force constant for springs are k1andk2. The time period of the suspended mass will be
View SolutionA mass is suspended separately by two springs and the time periods in the two cases are T1 and T2. Now the same mass is connected in parallel (K=K1+K2) with the springs and the time is suppose TP. Similarly time period in series is TS, then find the relation between T1,T2 and TP in the first case and T1,T2 and TS in the second case.
View SolutionWhen a body is suspended from two light springs separately, the periods of vertical oscillations are T1 and T2. When the same body is suspended from the two spring connected in series, the period will be
View SolutionA mass m is suspended from the two coupled springs connected in series. The force constant for spring are k1 and k2. The time period of the suspended mass will be:
View SolutionA mass M is suspended by two springs of force constants K1andK2 respectively as shown in the diagram. The total elongation (stretch) of the two springs is

View Solution