
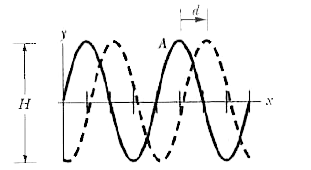
A sinusoidal wave moving along a string is shown twice in the figure. As crest A travels in the positive direction of an x axis by distance d=6.0 cm in 4.0m. The tick marks along the axis are separated by 10cm, height H=6.00mm. The wave equation is
y=(3mm)sin[16x−2.4×102t]
y=(3mm)sin[16x+2.4×102t]
y=(3mm)sin[8x+2.4×102t]
y=(3mm)sin[8x−2.4×102t]
The correct Answer is:A
The amplitude A is half of the 6.00 mm vertical range shown in the figure, that is ,A=3.0mm
The speed of the wave is v=d/t=15m/s, where d=0.060m and t=0.0040s. The angular wave number is k=2πλ where λ=0.40m. Thus, k=(2π)/(λ)=16(rad)/(m). The angular frequency is found from
ω=kv=(16radm)(15ms)=2.4×102rad/s. We choose the minus sign (between kx and ωt) in the argument of the sine function because the wave is shown traveling to the right (in the +x direction). Therefore, with SI units understood, we obtain
y=Asin[kx−ωt]=(3mm)sin[16x−2.4×102t]
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Superposition And Interference23videos
WAVES AND ACOUSTICS
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Beats20videos
WAVES AND ACOUSTICS
- BOOK - A2ZCHAPTER - WAVES AND ACOUSTICSEXERCISE - Chapter Test30videos
WAVES AND ACOUSTICS
- BOOK - A2ZCHAPTER - VECTORSEXERCISE - Chapter Test29videos
VECTORS
- BOOK - A2ZCHAPTER - WORK, ENERGY, POWER AND COLLISIONEXERCISE - Chapter Test29videos
WORK, ENERGY, POWER AND COLLISION
Similar Questions
In Fig 16-46, a sinusoidal wave moving along a string is shown twice as crest A travels in the positive direction of any x axis by distance d=6.0 cm in 3.0 ms. The tick marks along the axis are separated by 10cm, height H=6.00MM. The equation for the wave is in the form y(x,t) =ymsin(kx±ωt). so what are (a) ym,(b)k,(c)ω and (d) the correct choice of sign in front of ω?
 View Solution
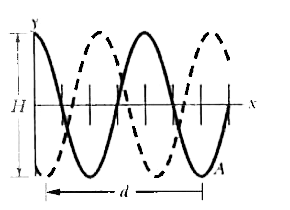
View SolutionTwo sinusoidal waves with the same amplitude of 6.00 mm and the same wavelength travel together along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16 39. as velley travels in the negative direction of the x axis by distance d= 56.0 cm in 8.0 ms. The lick matks along the axis are separated by 10cm, and height H is 8.0mm. Let the equation for one wive be of the form y(x,t) =ymsin(kx±ωt+ϕ1), where ϕ1=0 and you must choose the correct sign in front of ω. For the equation for the other wave, what are (a) ym,(b)k,(c)ω,(d)ϕ2, and (e) the sign in front of ω?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The equation of a simple harmonic progressive wave along the positive direction of X axis is given by
Ay=asin2π[tT−xλ]By=asin(2πnt)Cy=asin2π[tT+xλ]Dy=acos(2πnt) - Question 2 - Select One
An electromagnetic wave is traveling in the positive x direction with its electric filed along the z axis and its magnetic field along the y axis . The fields are related by
A∂E∂x=μ0ε0∂B∂xB∂E∂x=μ0ε0∂B∂tC∂B∂x=μ0ε0∂E∂tD∂B∂x=μ0ε0∂E∂t - Question 3 - Select One
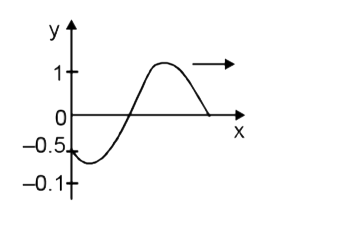
the equation of a wave travelling along the positive x - axis ,as shown in figure at t = 0 is given by
 Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
Asin(kx−ωt+π6)Bsin(kx−ωt−π6)Csin(ωt−kx+π6)Dsin(ωt−kx−π6)
Two sinusoidal waves with the same amplitude and wavelength travel through each other along a string that is stretched along an x axis. Their resultant wave is shown twice in Fig. 16-53, as the antinode A travels from an extreme upward displacement to an extreme downward displacement in 6.0 ms. The tick marks along the axis are separated by 15 cm, height H is 1.20 cm. Let the equation for one of the two waves be of the form y(x,t)=ymsin(kx+ω). In the equation for the other wave, what are (a)ym(b)k,(c)ω, and (d) the sign in front of ω?
 View Solution
View SolutionThe equation of a wave travelling along the positive x-axis, as shown in figure at t=0 is given by
 View Solution
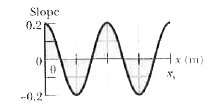
View SolutionA sinusoidal wave travels along a string under tension. Figure 16-52 gives the slopes along the string at time t=0. The scale of the x axis is st by xs=0.40m What is the amplitude of the wave?
 View Solution
View Solutionvx is the velocity of a particle moving along the x-axis as shown in the figure. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s ?
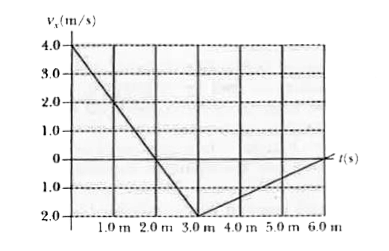 View Solution
View SolutionFor a particle moving along x-axis, a scaled x-6 graph is shown in figure. Mark the correct statement (s).
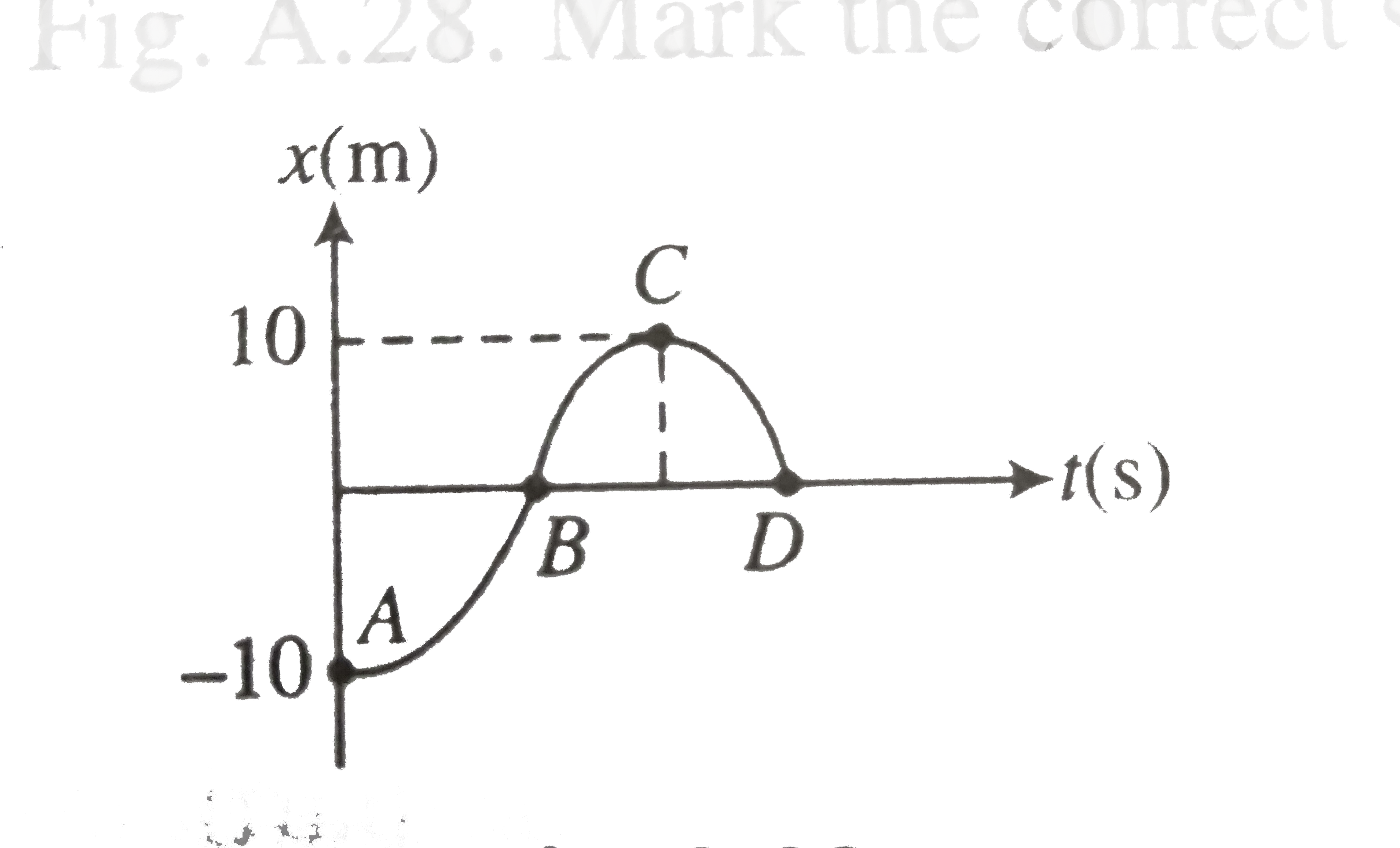 View Solution
View Solution

