Two object, each of mass 1.5kg, are moving in the same straight line but in opposite directions, The velocity of each object is 2.5ms−1 before the collision during which they stick together. What will be the velocity of the combined object after collision?
To solve the problem of two objects colliding and sticking together, we will use the principle of conservation of momentum. Here’s a step-by-step solution:
Step 1: Identify the masses and velocities of the objects
- Mass of object 1, m1=1.5kg
- Velocity of object 1, v1=2.5m/s (let's assume this is in the positive direction)
- Mass of object 2, m2=1.5kg
- Velocity of object 2, v2=−2.5m/s (since it is moving in the opposite direction)
Step 2: Calculate the initial momentum of both objects
The total initial momentum pinitial can be calculated using the formula:
pinitial=m1⋅v1+m2⋅v2
Substituting the values:
pinitial=(1.5kg⋅2.5m/s)+(1.5kg⋅−2.5m/s)
Calculating each term:
pinitial=3.75kg m/s−3.75kg m/s=0kg m/s
Step 3: Apply the conservation of momentum
According to the conservation of momentum, the total momentum before the collision is equal to the total momentum after the collision:
pinitial=pfinal
Let V be the final velocity of the combined mass after the collision. The combined mass after the collision is:
mcombined=m1+m2=1.5kg+1.5kg=3kg
Thus, the final momentum can be expressed as:
pfinal=mcombined⋅V=3kg⋅V
Step 4: Set the initial momentum equal to the final momentum
Since we calculated that the initial momentum is 0:
0=3kg⋅V
Step 5: Solve for the final velocity V
To find V:
V=03kg=0m/s
Conclusion
The velocity of the combined object after the collision is 0m/s. This means that after the collision, the two objects come to rest.
---
- Mass of object 1, m1=1.5kg
- Velocity of object 1, v1=2.5m/s (let's assume this is in the positive direction)
- Mass of object 2, m2=1.5kg
- Velocity of object 2, v2=−2.5m/s (since it is moving in the opposite direction)
The total initial momentum pinitial can be calculated using the formula:
pinitial=m1⋅v1+m2⋅v2
Substituting the values:
pinitial=(1.5kg⋅2.5m/s)+(1.5kg⋅−2.5m/s)
Calculating each term:
pinitial=3.75kg m/s−3.75kg m/s=0kg m/s
According to the conservation of momentum, the total momentum before the collision is equal to the total momentum after the collision:
pinitial=pfinal
Let V be the final velocity of the combined mass after the collision. The combined mass after the collision is:
mcombined=m1+m2=1.5kg+1.5kg=3kg
Thus, the final momentum can be expressed as:
pfinal=mcombined⋅V=3kg⋅V
Since we calculated that the initial momentum is 0:
0=3kg⋅V
To find V:
V=03kg=0m/s
The velocity of the combined object after the collision is 0m/s. This means that after the collision, the two objects come to rest.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - SHORT ANSWER QUESTIONS44videos
FORCES AND LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - LONG ANSWER QUESTIONS10videos
FORCES AND LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MOCK TEST36videos
FORCES AND LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - FLOTATIONEXERCISE - Problem For Practice6videos
FLOTATION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Model Test paper (1)36videos
GRAVITATION
Similar Questions
Two object, each of mass 1.5kg, are moving in the same straight line but in opposite directions, The velocity of each object is 2.5ms−1 before the collision during which they stick together. What will be the velocity of the combined object after collision?
View SolutionTwo objects each of mass 5 kg are moving in the same straight line but in the opposite direction towards each other with some speed of 3 m/s. They stick to each other after collision. What will be the velocity of the combined object after collision?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
There is a head on collision between two bodies A and B. The mass of A is 5 kg and it is moving with a velocity of 4m/s towards right. The mass of B is 4 kg and it is moving with a velocity of 5m/s in the opposite direction. After collision, they stick together. What is their common velocity after collision?
A1 m/s towards leftB54 m/s towards rightC45 m towards leftDzero
Two objects each of mass 5 kg are moving in the same straight line but in the opposite direction towards each other with some speed of 3 m/s. They stick to each other after collision. What will be the velocity of the combined object after collision?
 View Solution
View SolutionTwo objects m1andm2 are moving in the straight line approaching each other as shown. After collisions these objects together. What will be the velocity of the combined object after collisions?
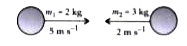 View Solution
View SolutionTwo object A and B are moving along the same straight line in opposite directions with velocities 10m/s and 5m/s respectively. They collide during which they stick to each other. If mass of A is 1.5kg and mass of B is 1kg, what is the velocity of the combinations?
View SolutionA block of mass 5 kg moves from left to right with a velocity of 2ms−1 and collides with another block of mass 3 kg moving along the same line in the opposite direction with velocity 4ms−1.
(i) If the collision is perfectly elastic, determine velocities of both the blocks after their collision.
(ii) If coefficient of restitution is 0.6, determine velocities of both the blocks after their collision.View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View SolutionTwo objects of masses 100g and 200g are moving along the same line in the same line in the same direction with velocities of 2m/s and 1m/s, respectively. They collide and after the collison, the first object moves at a velocity of 1.67m/s in the same direction. Determine the velocity of the second object.
View SolutionTwo spheres made of clay of masses 'm1' and 'm2' moving along a straight line in the same direction collide with each other. Their velocities just before collision are 'u1' and 'u2' respectively. After collision, they stick together and move with teh same velocity, in the same direction, along the straight line. Find the velocity with which they move together.
View Solution

