Three identical blocks, each having a mass , are pushed by a force on a frictionless table as shown in (figure) What is the acceleration of the blocks? What is net force on block ? What force does apply on ? What force does apply on ? show action reaction pairs on the contact surface of the blocks.
To solve the problem step by step, we will analyze the situation involving three identical blocks on a frictionless table being pushed by a force F.
Step 1: Calculate the Total Mass
The total mass of the three blocks can be calculated as follows:
- Each block has a mass M.
- Therefore, the total mass Mtotal=M+M+M=3M.
Step 2: Calculate the Acceleration of the Blocks
Using Newton's second law of motion, which states that F=ma, we can find the acceleration a of the blocks.
- The total force applied is F.
- The total mass is 3M.
- Therefore, we can write the equation:
F=(3M)⋅a
- Rearranging the equation to solve for acceleration a:
a=F3M
Step 3: Calculate the Net Force on Block A
The net force acting on block A can be calculated using the formula Fnet=ma.
- The mass of block A is M.
- The acceleration we found in Step 2 is F3M.
- Therefore, the net force on block A is:
Fnet, A=M⋅a=M⋅F3M=F3
Step 4: Calculate the Force that Block A Applies on Block B
To find the force that block A applies on block B, we consider the combined mass of blocks B and C.
- The mass of blocks B and C together is 2M.
- The acceleration is still F3M.
- The force that block A applies on block B is:
FA→B=(2M)⋅a=(2M)⋅F3M=2F3
Step 5: Calculate the Force that Block B Applies on Block C
Similarly, to find the force that block B applies on block C:
- The mass of block C is M.
- The acceleration is F3M.
- The force that block B applies on block C is:
FB→C=M⋅a=M⋅F3M=F3
Step 6: Identify Action-Reaction Pairs
According to Newton's third law, for every action, there is an equal and opposite reaction. The action-reaction pairs on the contact surfaces of the blocks are:
- The force that block A applies on block B (FA→B) is equal and opposite to the force that block B applies on block A (FB→A).
- The force that block B applies on block C (FB→C) is equal and opposite to the force that block C applies on block B (FC→B).
Summary of Results
1. Acceleration of the blocks: a=F3M
2. Net force on block A: Fnet, A=F3
3. Force that A applies on B: FA→B=2F3
4. Force that B applies on C: FB→C=F3
The total mass of the three blocks can be calculated as follows:
- Each block has a mass M.
- Therefore, the total mass Mtotal=M+M+M=3M.
Using Newton's second law of motion, which states that F=ma, we can find the acceleration a of the blocks.
- The total force applied is F.
- The total mass is 3M.
- Therefore, we can write the equation:
F=(3M)⋅a
- Rearranging the equation to solve for acceleration a:
a=F3M
The net force acting on block A can be calculated using the formula Fnet=ma.
- The mass of block A is M.
- The acceleration we found in Step 2 is F3M.
- Therefore, the net force on block A is:
Fnet, A=M⋅a=M⋅F3M=F3
To find the force that block A applies on block B, we consider the combined mass of blocks B and C.
- The mass of blocks B and C together is 2M.
- The acceleration is still F3M.
- The force that block A applies on block B is:
FA→B=(2M)⋅a=(2M)⋅F3M=2F3
Similarly, to find the force that block B applies on block C:
- The mass of block C is M.
- The acceleration is F3M.
- The force that block B applies on block C is:
FB→C=M⋅a=M⋅F3M=F3
According to Newton's third law, for every action, there is an equal and opposite reaction. The action-reaction pairs on the contact surfaces of the blocks are:
- The force that block A applies on block B (FA→B) is equal and opposite to the force that block B applies on block A (FB→A).
- The force that block B applies on block C (FB→C) is equal and opposite to the force that block C applies on block B (FC→B).
1. Acceleration of the blocks: a=F3M
2. Net force on block A: Fnet, A=F3
3. Force that A applies on B: FA→B=2F3
4. Force that B applies on C: FB→C=F3
Topper's Solved these Questions
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:VALUE BASED QUESTIONS
Explore 4 Videos
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:EXERCISE
Explore 24 Videos
- FORCES AND LAWS OF MOTIONBook:PRADEEPChapter:FORCES AND LAWS OF MOTIONExercise:VERY SHORT ANSWER QUESTIONS
Explore 29 Videos
- FLOTATIONBook:PRADEEPChapter:FLOTATIONExercise:Problem For Practice
Explore 6 Videos
- GRAVITATIONBook:PRADEEPChapter:GRAVITATIONExercise:Model Test paper (1)
Explore 36 Videos
Similar Questions
Three identical blocks each of mass M are along a frictionless table and a force F is acting as shown. Which of the following statements is false ?
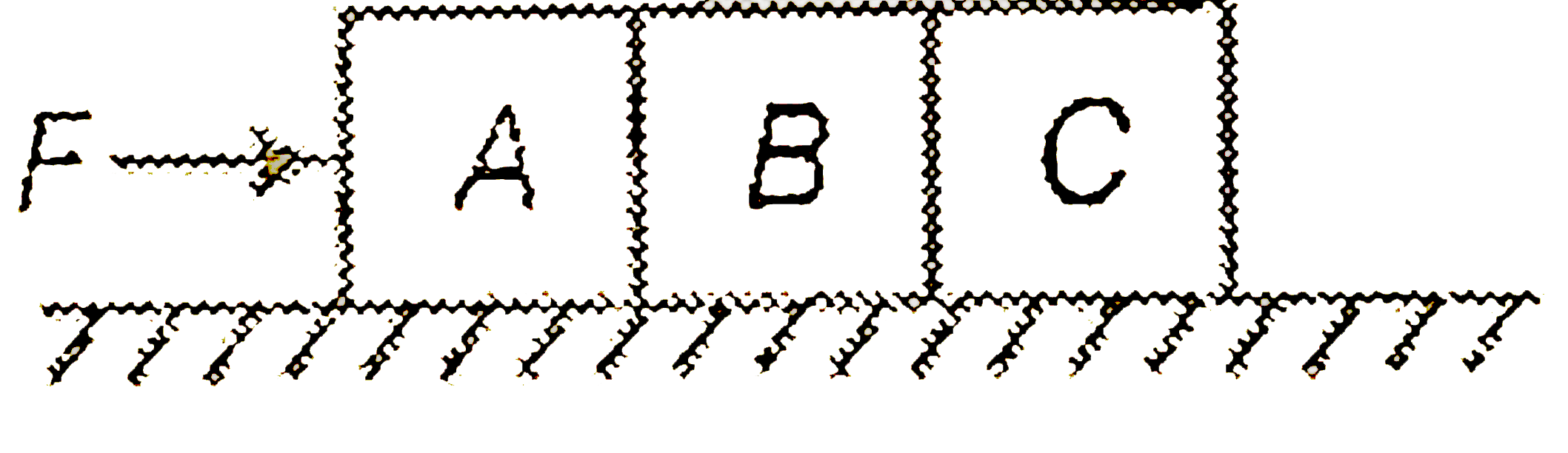
View SolutionThree identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What is the net force on the block A?

View Solution
Knowledge Check
Three identical blocks of masses m=2kg are drawn by a force 10.2 N on a frictionless surface. What is the tension (in N) in the string between the blocks B and C?
 A9.2B8C3.4D9.8
A9.2B8C3.4D9.8Two forces act on a 4.5 kg block resting on a frictionless surface as shown in the given figure. What is the magnitude of the horizontal acceleration of the block ?
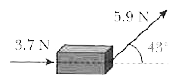 A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2
A1.8 m/s2B1.2 m/s2C0.82 m/s2D3.2 m/s2A block of mass √3kg rests on a horizontal frictionless surface. What will be the acceleration of the block if it is subjected to two forces as shown in the figure.
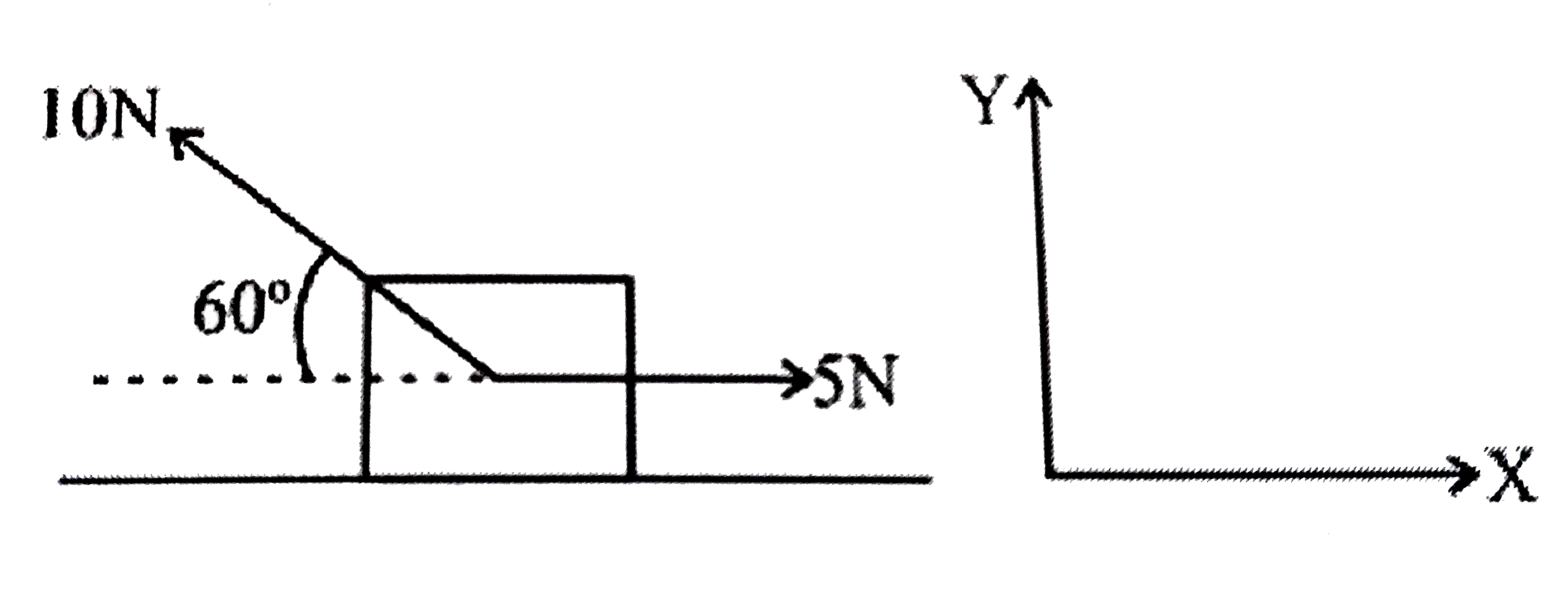 AAcceleration will be along Y-axisBAcceleration will be along X-axisCAcceleration will be in between X & YDNo acceleration will be there
AAcceleration will be along Y-axisBAcceleration will be along X-axisCAcceleration will be in between X & YDNo acceleration will be there
Three identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What force does B apply on C?

View SolutionThree identical blocks, each having a mass m are pushed by a force F on the Frictionless table as shown in figure.
What force does A apply on B?

View SolutionA horizontal force of 4 N is applied to a block of mass 2 kg resting on a frictionless table. What is the acceleration of the block in ms−2 ?
View SolutionFind the contact force between the block and acceleration of the blocks as shown in figure.
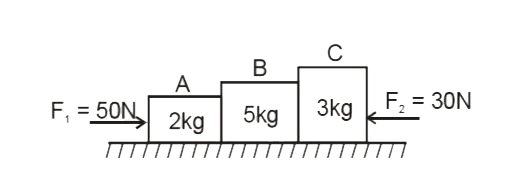
View SolutionThree identical blocks of masses m=2kg are drawn by a force F=10.2N with an acceleration of 0.6ms−2 on a frictionless surface, then what is the tension (in N) in the string between the blocks B and C?

View Solution