A bullet of mass 20gram moving with a velocity of 300m/s gets embedded in a freely suspened wooden block of mass 880gram. What is the velocity acquired by the blocks?
To solve the problem, we will use the principle of conservation of momentum. According to this principle, the total momentum before an event must equal the total momentum after the event, provided no external forces act on the system.
1. Identify the masses and velocities:
- Mass of the bullet (m1) = 20 grams = 20 × 10^(-3) kg (since 1 gram = 10^(-3) kg)
- Velocity of the bullet (v1) = 300 m/s
- Mass of the wooden block (m2) = 880 grams = 880 × 10^(-3) kg
- Initial velocity of the wooden block (v2) = 0 m/s (since it is at rest)
2. Calculate the initial momentum of the system:
- Initial momentum (p_initial) = momentum of the bullet + momentum of the block
- p_initial = (m1 * v1) + (m2 * v2)
- p_initial = (20 × 10^(-3) kg * 300 m/s) + (880 × 10^(-3) kg * 0 m/s)
- p_initial = 6000 × 10^(-3) kg·m/s
- p_initial = 6 kg·m/s
3. Calculate the total mass after the bullet embeds in the block:
- Total mass (m_total) = m1 + m2
- m_total = (20 × 10^(-3) kg) + (880 × 10^(-3) kg)
- m_total = 900 × 10^(-3) kg
- m_total = 0.9 kg
4. Let the final velocity of the combined mass (v_final) be what we need to find.
- According to the conservation of momentum:
- p_initial = p_final
- p_final = m_total * v_final
- Therefore, 6 kg·m/s = (0.9 kg) * v_final
5. Solve for v_final:
- v_final = 6 kg·m/s / 0.9 kg
- v_final = 20/3 m/s
- v_final ≈ 6.67 m/s
Final Answer:
The velocity acquired by the block after the bullet embeds in it is approximately 6.67 m/s.
---
- Mass of the bullet (m1) = 20 grams = 20 × 10^(-3) kg (since 1 gram = 10^(-3) kg)
- Velocity of the bullet (v1) = 300 m/s
- Mass of the wooden block (m2) = 880 grams = 880 × 10^(-3) kg
- Initial velocity of the wooden block (v2) = 0 m/s (since it is at rest)
- Initial momentum (p_initial) = momentum of the bullet + momentum of the block
- p_initial = (m1 * v1) + (m2 * v2)
- p_initial = (20 × 10^(-3) kg * 300 m/s) + (880 × 10^(-3) kg * 0 m/s)
- p_initial = 6000 × 10^(-3) kg·m/s
- p_initial = 6 kg·m/s
- Total mass (m_total) = m1 + m2
- m_total = (20 × 10^(-3) kg) + (880 × 10^(-3) kg)
- m_total = 900 × 10^(-3) kg
- m_total = 0.9 kg
- According to the conservation of momentum:
- p_initial = p_final
- p_final = m_total * v_final
- Therefore, 6 kg·m/s = (0.9 kg) * v_final
- v_final = 6 kg·m/s / 0.9 kg
- v_final = 20/3 m/s
- v_final ≈ 6.67 m/s
The velocity acquired by the block after the bullet embeds in it is approximately 6.67 m/s.
Topper's Solved these Questions
- FORCES AND LAWS OF MOTIONBOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - ORAL TESTING
20 Videos
- FORCES AND LAWS OF MOTIONBOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - QUIZ TESTING
12 Videos
- FORCES AND LAWS OF MOTIONBOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - VALUE BASED QUESTIONS
4 Videos
- FLOTATIONBOOK - PRADEEPCHAPTER - FLOTATIONEXERCISE - Problem For Practice
6 Videos
- GRAVITATIONBOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Model Test paper (1)
36 Videos
Similar Questions
A bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is

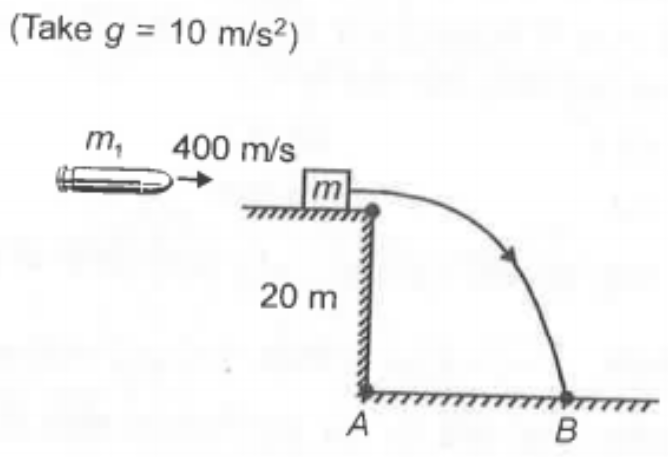
View SolutionA bullet of mass 0.05 kg moving with velocity 400 m/s gets embedded after collision with a block of mass 3.95 kg placed on a smooth horizontal platform as shown in the figure. If height of the platform from the ground is 20 m and block strikes the ground at B, then the value of AB is
View Solution
Knowledge Check
A bullet of mass 10 g moving with a velocity of 400 m/s gets embedded in a freely suspended wooden block of mass 900 g. What is the velocity acquired by the block ?
 A44 m/sB4.4 m/sC0.44 m/sD440 m/s
A44 m/sB4.4 m/sC0.44 m/sD440 m/sA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 A√2ghBM+mm√ghCmM+m2ghDM+mM√2gh
A√2ghBM+mm√ghCmM+m2ghDM+mM√2ghA bullet of mass m moving with velocity υ1 strikes a suspended wooden block of mass M as shown in the figure and sticks to it. If the block rises to a height y. the initial of the bullet is
 A√2ghBM+mm√2ghCmM+m2ghDM+mM√2gh
A√2ghBM+mm√2ghCmM+m2ghDM+mM√2gh
A bullet of mass m moving with a speed v strikes a wooden block of mass M & gets embedded into the block. The final speed is
View SolutionA bullet of mass 50 gram is fired from a 5 kg gun with a velocity of 1 km/s . the speed of recoil of the gun is
View SolutionA bullet of mass 10 gm moving with a horizontal velocity 100m/s passes through a wooden block of mass 100 gm. The block is resting on a smooth horizontal floor. After passing through the block the velocity of the bullet is 10m/s. the velocity of the emerging bullet with respect to the block is
View SolutionA bullet of mass 0.04 kg moving with a speed of 600 m/s penetrates a heavy wooden block. It stops after a penetration of 500 cm. The resistive force exerted by the block on the bullet is
View SolutionA bullet of mass 50 gram is fired from a 5 kg gun with a velocity of 1 km/s . the speed of recoil of the gun is
View Solution
