Two satelites of a planet have period 32 days and 256 days. If the radius of orbit of former is R, find the orbital radius of the latter.
The correct Answer is:4R
To solve the problem of finding the orbital radius of the second satellite given the period of both satellites, we can use Kepler's Third Law of Planetary Motion, which states that the square of the period of a satellite is directly proportional to the cube of the semi-major axis of its orbit.
1. Identify the Given Values:
- Period of the first satellite (T1) = 32 days
- Period of the second satellite (T2) = 256 days
- Radius of the first satellite's orbit (R1) = R (unknown value)
- Radius of the second satellite's orbit (R2) = ? (to be found)
2. Apply Kepler's Third Law:
According to Kepler's Third Law:
T21T22=R31R32
3. Substitute the Known Values:
Substitute T1 and T2 into the equation:
(32)2(256)2=R3R32
4. Calculate the Left Side:
Calculate 322 and 2562:
322=1024
2562=65536
Therefore:
102465536=R3R32
5. Simplify the Fraction:
Simplifying 102465536:
102465536=164
So we have:
164=R3R32
6. Cross Multiply:
Cross multiplying gives:
R32=64R3
7. Take the Cube Root:
Taking the cube root of both sides:
R2=R⋅4
8. Final Answer:
The orbital radius of the second satellite is:
R2=4R
Summary:
The orbital radius of the second satellite is four times the radius of the first satellite.
- Period of the first satellite (T1) = 32 days
- Period of the second satellite (T2) = 256 days
- Radius of the first satellite's orbit (R1) = R (unknown value)
- Radius of the second satellite's orbit (R2) = ? (to be found)
According to Kepler's Third Law:
T21T22=R31R32
Substitute T1 and T2 into the equation:
(32)2(256)2=R3R32
Calculate 322 and 2562:
322=1024
2562=65536
Therefore:
102465536=R3R32
Simplifying 102465536:
102465536=164
So we have:
164=R3R32
Cross multiplying gives:
R32=64R3
Taking the cube root of both sides:
R2=R⋅4
The orbital radius of the second satellite is:
R2=4R
The orbital radius of the second satellite is four times the radius of the first satellite.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Oral testing16videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Quiz testing10videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - GRAVITATIONEXERCISE - Value Based Questions4videos
GRAVITATION
- BOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MOCK TEST36videos
FORCES AND LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - MOTIONEXERCISE - Mock test24videos
MOTION
Similar Questions
Find the mass of the Earth knowing the orbital period and the radius of the Moon.
View SolutionAn artificial satellite of mass m is revolving in a circualr orbit around a planet of mass M and radius R. If the radius of the orbit of satellite be r, then period of satellite is
T=2πR√r3g
Justify the relation using the method of dimensions.View Solution
Knowledge Check
- Question 1 - Select One
The radius of a planet is 74×103km. A satellite of this planet completes one revolution in 16.7 days. If the radius of the orbit of satellite is 27 times the radius of planet, then the mass of planet is
A2.3×1027kgB2.3×1030kgC2.3×1032kgD2.3×1042kg - Question 2 - Select One
If the radius of first Bohr's orbit is r, then radius of second orbit will be
A2rBr2C4rD√2r - Question 3 - Select One
If r is the radius of first orbit, the radius of nth orbit of the H atom will be:
Arn2BrnCrnDr2n2
If a satellite is revolving around a planet of mass M in an elliptical orbit of semi-major axis a. Show that the orbital speed of the satellite when it is at a distance r from the planet will be given by v2=GM[2r−1a]
View SolutionTwo planets revolve with same angular velocity about a star. The radius of orbit of outer planet is twice the radius of orbit of the inner planet. If T is time period of the revolution of outer planet, find the time in which inner planet will fall into the star. If it was suddenly stopped.
View SolutionThe orbital velocity of a satellite at point B with radius rB and n. The radius of a point A is rA. If the orbit is increased in radial distance so that rA becomes .12rA find the orbital velocity at (1.2rA):
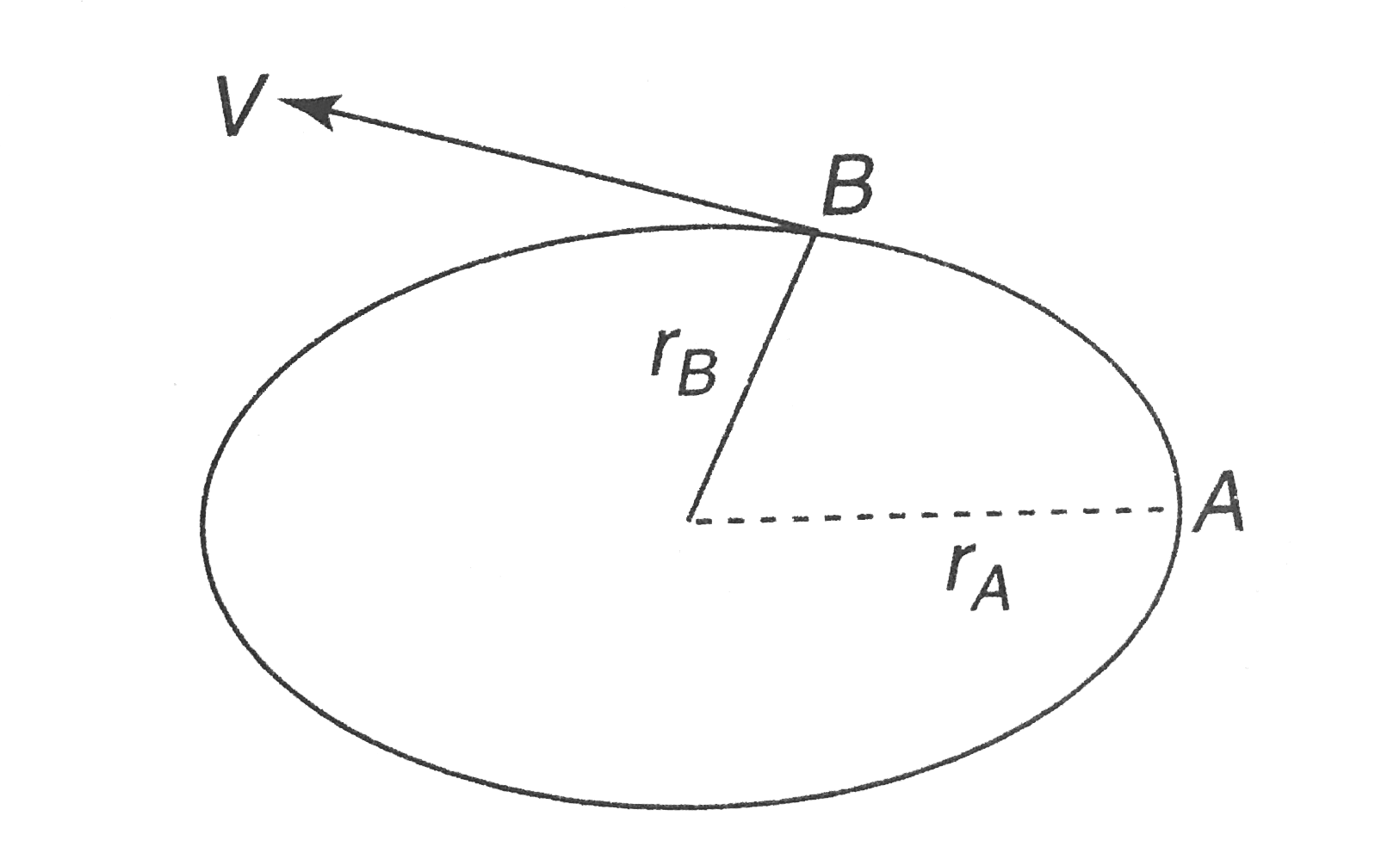 View Solution
View SolutionThe period of a planet around sun is 27 times that of earth the ratio of radius of planet orbit to the radius of earth's orbit is
View SolutionThe work done to increases the radius of orbit of a satellite of mass 'm' revolving around a planet of mass M from orbit of radius R into another orbit of radius 3R is
View Solution

