A cubical block of water is dipped completely in water. Each edge of the block is 1 cm is length. Find the bouyant force acting on the block.
Here, volume of the block, V=1cm×1cm×1cm=1cm3=10−6m3
mass of water displaces, M=V×d=(10−6m3)(100kgm3)=10−3kg
weight of water displaced Wi=Mg=(10−3kg)(10ms)=10−2N
Buoyant force acting on the block i.e., FB=Wi=10−2N
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - FLOTATIONEXERCISE - PROBLEMS FOR PRACTICE18videos
FLOTATION
- BOOK - PRADEEPCHAPTER - FLOTATIONEXERCISE - ASSESSMENT THROUGH PAPER-PEN TEST30videos
FLOTATION
- BOOK - PRADEEPCHAPTER - FLOTATIONEXERCISE - Value Based Questions4videos
FLOTATION
- BOOK - PRADEEPCHAPTER - FORCES AND LAWS OF MOTIONEXERCISE - MOCK TEST36videos
FORCES AND LAWS OF MOTION
Similar Questions
Knowledge Check
- Question 1 - Select One
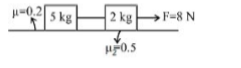
Find fiction force acting on 2 kg block.A10 NB2NC8ND0N - Question 2 - Select One
As shown in the figure , the friction force acting on the block is
 A50NB30NC20NDNone
A50NB30NC20NDNone - Question 3 - Select One
If coefficient of friction between both the block is μ−12 . Find friction force acting between both block.
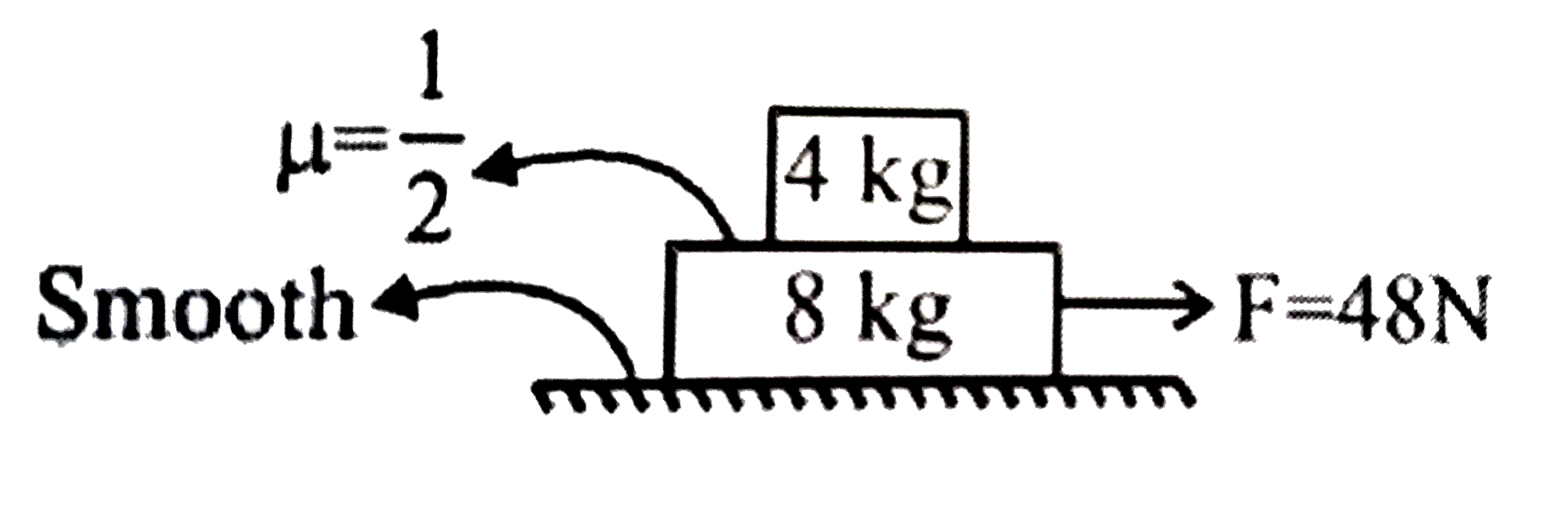 A16NB20NC8ND10N
A16NB20NC8ND10N
The frictional force acting on 1 kg block is
 View Solution
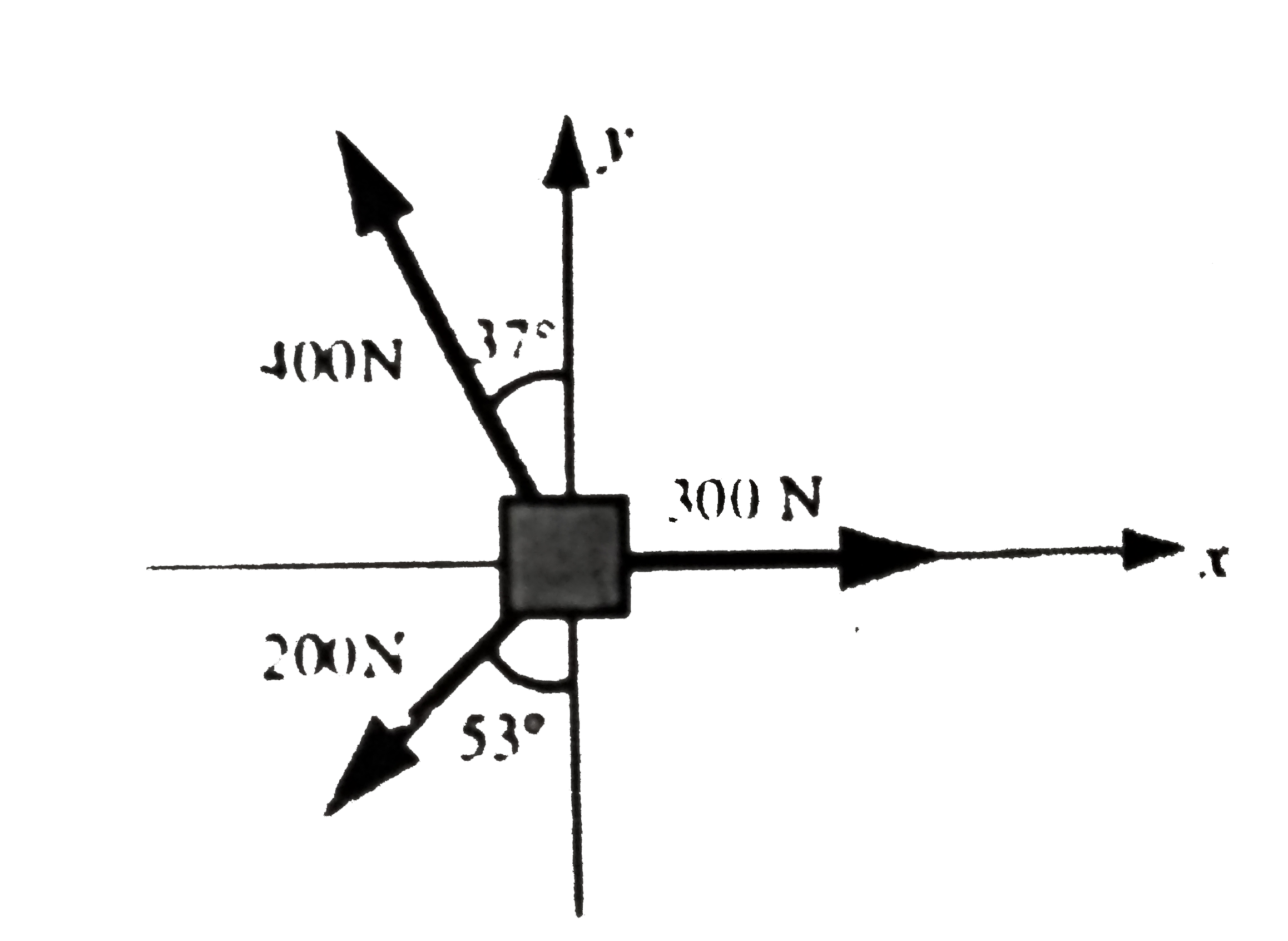
View SolutionA block is placed on a rough horizontal plane. Three horizontalforces are applied on the block as shown in the figure. If the block is in equilibrium, find the friction force acting on the block.
 View Solution
View SolutionA block of mass m is kept on a horizontal table. If the static friction coefficient is μ., find the frictional force acting on the block.
View SolutionFigure shows a string stretched by a block going over a pulley. The string vibrates in its tenth harmonic in unison with a particular tuning fork. When a beaker containing water is brought under the block so that the block is completely dipped into the beaker, the string vibrates in its eleventh harmonic. Find the density of the material of the block.
 .View Solution
.View SolutionA tank contains water on top of mercury as shown in figure. A cubical block of side 10 cm is in equilibrium inside the tank. The depth of the block inside mercury is (RD of the material of block =8.56, RD of mercury =13.6)
 View Solution
View Solution


