Explain how will you measure (i) the size of astronomical object and (ii) the distance of a nearby star.
To measure the size of an astronomical object and the distance of a nearby star, we can follow these steps:
(i) Measuring the Size of an Astronomical Object
1. Use of Telescopes: The first step is to utilize a telescope, which allows us to observe distant astronomical objects clearly. Telescopes can gather more light than the human eye, making faint objects visible.
2. Determine the Angular Size: When observing an astronomical object, we can determine its angular size (θ) in the sky. This is the angle that the object appears to span from our viewpoint on Earth.
3. Calculate the Actual Size: To find the actual size (D) of the object, we can use the formula:
D=d⋅θ
where d is the distance to the astronomical object and θ is in radians. If the angle is given in degrees, we need to convert it to radians by using:
radians=degrees×π180
(ii) Measuring the Distance of a Nearby Star
1. Parallax Method: To measure the distance of a nearby star, we use the parallax method. This involves observing the star from two different positions in Earth's orbit around the Sun.
2. Measure the Baseline: The baseline (B) is the distance between the two observation points on Earth, typically the diameter of Earth's orbit (about 2 AU, where 1 AU is the average distance from the Earth to the Sun).
3. Observe the Parallax Angle: As we observe the star from these two positions, we measure the angle (θ) formed at the star by the two observation points. This angle is known as the parallax angle.
4. Calculate the Distance: The distance (D) to the star can be calculated using the formula:
D=B2⋅tan(θ2)
For small angles, we can approximate tan(θ)≈θ (in radians), leading to:
D≈Bθ
Summary
- To measure the size of an astronomical object, we use telescopes to determine the angular size and apply the distance to calculate the actual size.
- To measure the distance to a nearby star, we utilize the parallax method, measuring the parallax angle from two different positions on Earth.
D=d⋅θ
where d is the distance to the astronomical object and θ is in radians. If the angle is given in degrees, we need to convert it to radians by using:
radians=degrees×π180
D=B2⋅tan(θ2)
For small angles, we can approximate tan(θ)≈θ (in radians), leading to:
D≈Bθ
- To measure the distance to a nearby star, we utilize the parallax method, measuring the parallax angle from two different positions on Earth.
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Very short Answer Questions
Explore 89 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Short Answer Question 2 marks
Explore 8 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Short answer Questions 3 marks
Explore 23 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:multiple choice Questions
Explore 13 Videos
- PROPERTIES OF BULK MATTERBook:PRADEEPChapter:PROPERTIES OF BULK MATTERExercise:Multiple choice questions
Explore 7 Videos
Similar Questions
Knowledge Check
What is the unit of measurement of the distance of stars from the earth?
ALight yearBFathomsCNautical milesDKilometresA convex mirror of focal length f produces an image (1n)th of the size of the object. Then the distance of the object from the mirror is
AnfB(n+1)fC(n-1)fD(nn+1)f
Explain how our eyes can detect both nearby and faraway objects.
View SolutionA parsec is a convenient unit of length on the astronomical scale. It is the distance of an object that will show a parallax of 1 (second) of arc from opposite ends of a baseline equal to the distance from the earth to the sun. How much is parsec in terms of metres ?
View SolutionWhat is meant by the apparent size of an object ? With a neat and labelled diagram, explain the relation between the apparent size of an object and the angle subtended by the object at the eye.
View SolutionGiven below as Figure 13.8 is the distance-time graph of the motion an object.
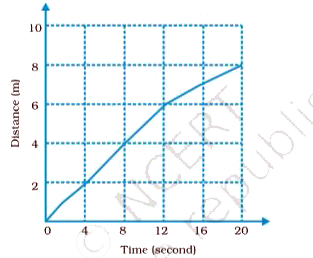
(i) What will be the position of the object at 20s?
(ii) What will be the distance travelled by the object in 12s?
(iii) What is the average speed of the object?
View SolutionExplain measurement of specific heat of solid object by mixing method.
View SolutionExplain measurement of specific heat of solid object by mixing method.
View Solution