Let I = current through a conductor, R =its resistance and V = potential difference across its ends. According to Ohm's law, product of two of these quantites equals the third. Obtain Ohm's law from dimensional analysis. Dimensional formula for R and V are [ML2T−3A−2]and[ML2T−2A−1] respectively.
Let V=IaTb
∴[ML2T−3A−1]=Aa[ML2T9−3)A−2]b=MbL2bT−3bAa−2b
Applying the principle of homogeneity of dimensions, we get
b = 1, 2b = 2, -3b = -3
a-2b = -1, a = -1 +2b = -1+ 2 =1
Putting these values in (i), we get
V=I1R1
This is Ohm's law.
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Value Based Questions
5 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Problems for Practice
130 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Curiosity Questions
7 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - multiple choice Questions
13 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
Similar Questions
Let I= current through a conductor, R= its resistance and V= potential difference across its ends. According to Ohm's law, product of two of these quantities equals the third. Obtain Ohm's law from dimensional analysis. Dimensonal formulae for R andV are ML2I−2T−3andML2T−3I−1 respectively.
View SolutionIf a current of 3 A flows through a wire of resistance 8 ohms, calculate the potential difference applied across its ends.
View Solution
Knowledge Check
The SI unit of a physical quantity having the dimensional formula of [ML^(0)T^(-2) A^(-1)]
AteslaBweberCamp metreDamp m2How much current is flowing through a 1kΩ resistor when a potential difference of 2 V is applied across its end ?
A2μAB2mAC2AD1AWhen a current I is passed through a wire of constant resistance, it produces a potential difference V across its ends. The graph drawn between log I and log V will be
A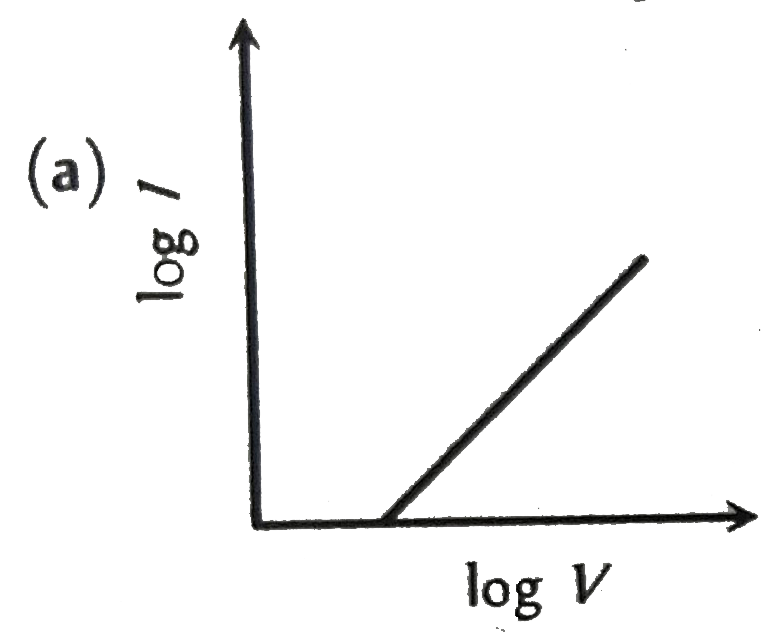 B
B C
C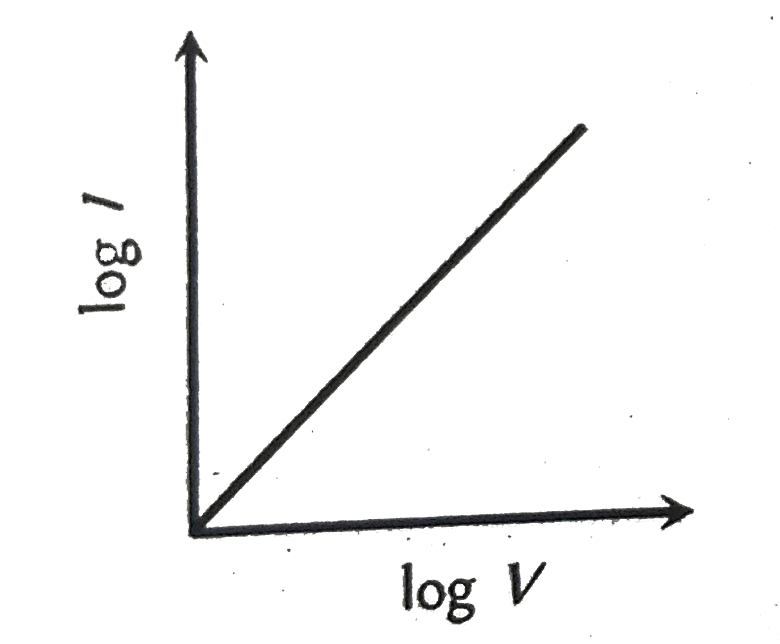 D
D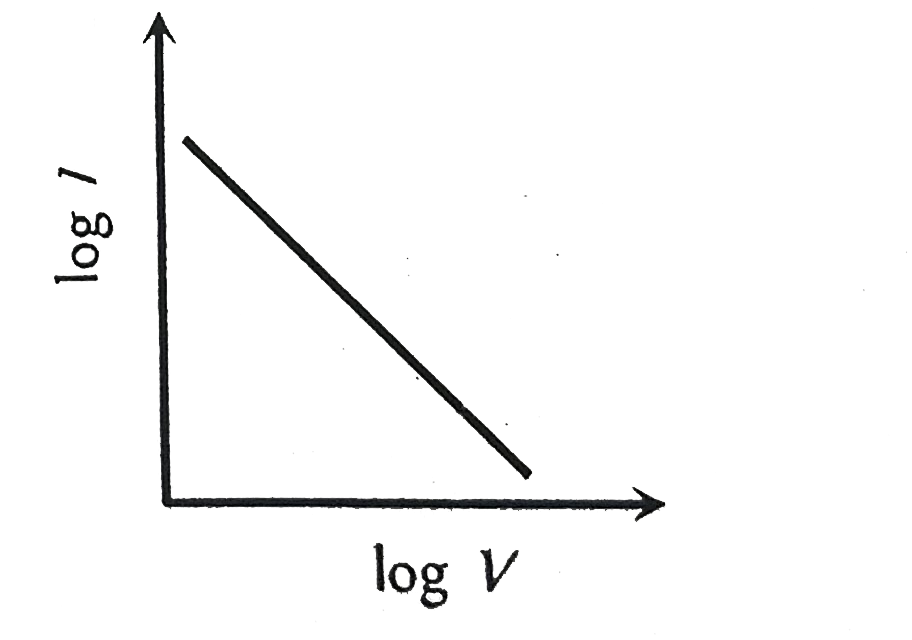
How much current flows through a 2 kΩ resistor when a potential difference of 4 V is applied across its ends ?
View SolutionHow much current flows through a 2kΩ resistor when a potential difference of 4V is applied across its ends?
View SolutionName the physical quantities that have dimensional formula [ML−1T−2].
View SolutionName the physical quantities whose dimensional formulae are as follows:ML2T−3
View Solution[ML−1T−2) is the dimensional formula of
View Solution