Expermients show that frequency (n) of a tuning fork depends on lentght (I) fo the prong, density (d) and the Young's modulus (Y) of its meterial. On the basis of dimensional analysis, dericve an expression for frequency of tunnig fork.
The correct Answer is:n=Kl√Yd
To derive an expression for the frequency (n) of a tuning fork based on the length (L) of its prong, density (d), and Young's modulus (Y) of its material using dimensional analysis, we can follow these steps:
Step 1: Identify the Variables
We know that the frequency n depends on:
- Length of the prong L
- Density of the material d
- Young's modulus of the material Y
Step 2: Write the Relationship
We can express the relationship as:
n=k⋅LA⋅dB⋅YC
where k is a dimensionless constant, and A, B, and C are the powers we need to determine.
Step 3: Write the Dimensions
Next, we need to write the dimensions of each variable:
- Frequency n has dimensions of (T−1)
- Length L has dimensions of (L)
- Density d has dimensions of (ML−3)
- Young's modulus Y has dimensions of (ML−1T−2)
Step 4: Substitute the Dimensions
Substituting the dimensions into the equation gives:
(T−1)=(L)A⋅(ML−3)B⋅(ML−1T−2)C
Expanding this, we have:
(T−1)=(L)A⋅(M)B⋅(L)−3B⋅(M)C⋅(L)−C⋅(T)−2C
Step 5: Combine the Dimensions
Combining the dimensions on the right side:
(T−1)=(M)B+C⋅(L)A−3B−C⋅(T)−2C
Step 6: Set Up the Equations
Now, we equate the powers of M, L, and T from both sides:
1. For mass M: B+C=0 (1)
2. For length L: A−3B−C=0 (2)
3. For time T: −2C=−1 (3)
Step 7: Solve the Equations
From equation (3):
C=12
Substituting C into equation (1):
B+12=0
B=−12
Now substitute B and C into equation (2):
A−3(−12)−12=0
A+32−12=0
A+1=0
A=−1
Step 8: Write the Final Expression
Now we have:
- A=−1
- B=−12
- C=12
Substituting these values back into the original equation:
n=k⋅L−1⋅d−12⋅Y12
Rearranging gives:
n=k⋅1L⋅√Yd
Final Expression
Thus, the expression for the frequency n of the tuning fork is:
n=k⋅1L⋅√Yd
We know that the frequency n depends on:
- Length of the prong L
- Density of the material d
- Young's modulus of the material Y
We can express the relationship as:
n=k⋅LA⋅dB⋅YC
where k is a dimensionless constant, and A, B, and C are the powers we need to determine.
Next, we need to write the dimensions of each variable:
- Frequency n has dimensions of (T−1)
- Length L has dimensions of (L)
- Density d has dimensions of (ML−3)
- Young's modulus Y has dimensions of (ML−1T−2)
Substituting the dimensions into the equation gives:
(T−1)=(L)A⋅(ML−3)B⋅(ML−1T−2)C
(T−1)=(L)A⋅(M)B⋅(L)−3B⋅(M)C⋅(L)−C⋅(T)−2C
Combining the dimensions on the right side:
(T−1)=(M)B+C⋅(L)A−3B−C⋅(T)−2C
Now, we equate the powers of M, L, and T from both sides:
1. For mass M: B+C=0 (1)
2. For length L: A−3B−C=0 (2)
3. For time T: −2C=−1 (3)
From equation (3):
C=12
B+12=0
B=−12
A−3(−12)−12=0
A+32−12=0
A+1=0
A=−1
Now we have:
- A=−1
- B=−12
- C=12
n=k⋅L−1⋅d−12⋅Y12
n=k⋅1L⋅√Yd
Thus, the expression for the frequency n of the tuning fork is:
n=k⋅1L⋅√Yd
Topper's Solved these Questions
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Test Your Grip
50 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Fill in the blanks
50 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Value Based Questions
5 Videos
- OSCILLATIONS AND WAVESBOOK - PRADEEPCHAPTER - OSCILLATIONS AND WAVESEXERCISE - multiple choice Questions
13 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
Similar Questions
The period of vibration of a tunign fork depends on the length I of its prong, density d and Young's modulus Y of the meterial. Deduce an expression for the period of vibration (T) using dimensional analysis.
View SolutionThe frequency of vibration of string depends on the length L between the nodes, the tension F in the string and its mass per unit length m. Guess the expression for its frequency from dimensional analysis.
View Solution
Knowledge Check
A tuning fork produces 6 beats/sec with sonometer wire when its tensions are either 169N or 196N. The frequency of that fork is
A162 HzB190 HzC200 HzD80 HzA tuning fork produces 6 beats/sec with sonometer wire when its tensions are either 169N or 196N. The frequency of that fork is
A162HzB190HzC200HzD80HzWhen two tuning forks A and B are sounded together x beats/s are heard. Frequency A is n. Now when one prong of B is loaded with a little wax, the number of beats/s decreases. The frequency of fork B is
An+xBn−xCn−x2Dn−2x
A vibrating string of certain length l under a tension T resonates with a mode corresponding to the first overtone (third harmonic ) of an air column of length 75cm inside a tube closed at one end. The string also generates 4beats/s with a tuning fork of frequency n . Now when the tension of the string is slightly increased the number of beats reduces to 2 per second. Assuming the velocity of sound in air to 340m/s , the frequency n the tuning fork in HZ is
(a) 344
(b) 336
(c ) 117.3
(d) 109.3
View SolutionState the formulae for the frequency N of a tuning fork in Melde's experiment (i) in perpendicular position and (ii) in paraller position, if L is the vibrating length of the string having linear density m and under tension T.
View SolutionThe energy E of an oscillating body is simple harmonic motion depends on its mass m, frequency n and emplitude a using the method of dimensional analysis find the relation between E ,m, n and a .
View SolutionA metal wire of diameter 1mm is held on two knife edges separated by a distance of 50cm . The tension in the wire is 100 N. the wire vibrates with its fundamental frequency and a vibrating tuning fork together produce 5 beat/s. The tension in the wire is the reduced to 81N. When the two are excited , beat are heard at the same rate, then the frequency of the fork will be ,
View SolutionFigure shown a clamped metal string of length 30cm and linear mass density 0.1kg/m. Which is taut at a tension of 40N. A small rider ( piece of paper ) is placed on string at point P as shown. An external vibrating tuning fork is brought near this string and oscillations of rider are carefully observed.
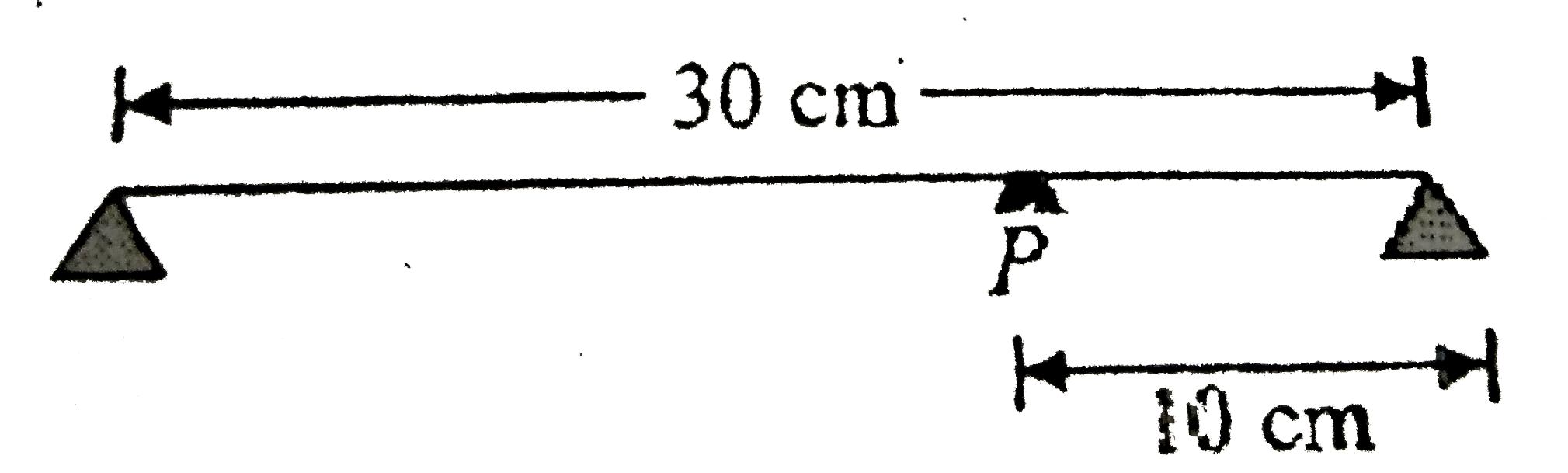
Now if the tensio in the string is made 160N, at which of the following frequencies of turning fork , rider will not vibrate at all
View Solution
