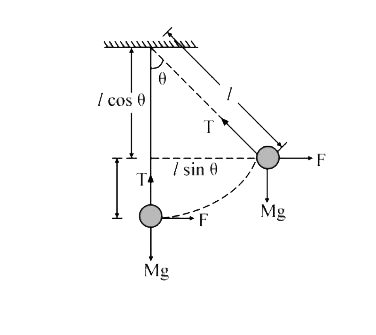
A mass of M kg is suspended by a weightless string. The horizontal force required to displace it until string makes an angle of 45∘ with the initial vertical direction is:
Mg√2
Mg(√2−1)
Mg(√2+1)
Mg√2
The correct Answer is:B
According to work energy theorem “work done by all forces is equal to change kinetic energy”.
∴Wtotal=ΔK
WF+Wgravity+WT=(Kfinal−Kinitial)=(0−0)=0
Work done by F,WF=F×lsin45∘=F1√2
Work done by gravity ,
Wgravity=−Mg(1−lcos45∘)=−Mgl(1−1√2)
Work done by tension = 0
∴F1√2+⎛⎜
⎜⎝−Mgl(√2−1)√2⎞⎟
⎟⎠=0 or F=Mg(√2−1) .
Similar Questions
Knowledge Check
A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
AMg(√2+1)BMg√2CMg√2DMg(√2−1)A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
AMg(√2+1)BMg√2CMg√2DMg(√2−1)A mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle of 45∘ with the initial vertical direction is
A(a) Mg(√2+1)B(b) Mg√2C(c) Mg√2D(d) Mg(√2−1)
Derermine the horizontal force required to displace a mass of 0.03kg suspended by a string until the string makes an angle 300 with the vertical.
View SolutionA body of mass √3 kg is suspended by a string to a rigid support. The body is pulled horizontally by a force F until the string makes an angle of 30° with the vertical. The value of F and tension in the string are.
View SolutionA mass of M kg is suspended by a weightless string. The horizontal force that is required to displace it until the string makes an angle 45∘ with the initial vertical direction is
View SolutionA body of mass √3 kg is suspended by a string to rigid support.The body is pulled horizontally by a force F until the string makes an angle of 30∘ with the vertical.The value of F and tension in the string are
View SolutionA mass of 10 kg is suspended from a spring balance, it is pulled aside by a horizontal string so that it makes an angle 60∘ with the vertical. The new reading of the balance is:
View Solution
