Two inclined planes (AB) and (BC) are placed as shown in Fig. 2 (ABC).3 A particle is projected from the foot of the plane of angle α along its line witn a velocity just sufficient to carry it to the top after which the particle slides down the other inclined plane. Fing the total time it will take to reach the pont (C ).
To solve the problem of finding the total time it takes for a particle projected from the foot of an inclined plane (AB) to reach point C after sliding down the second inclined plane (BC), we can break the problem into two parts: the time taken to ascend the first inclined plane and the time taken to descend the second inclined plane.
Step 1: Analyze the motion on the first inclined plane (AB)
1. Identify the parameters:
- Let the angle of inclination of plane AB be α.
- Let the height of plane AB be h.
- The initial velocity u is just sufficient to reach the top, which means at the top, the final velocity v=0.
2. Use the equations of motion:
- The motion can be analyzed using the equation:
v2=u2+2as
- Here, v=0 (at the top), a=−gsin(α) (the component of gravitational acceleration acting down the incline), and s=h/sin(α) (the distance along the incline).
3. Substituting the values:
0=u2−2gsin(α)⋅hsin(α)
Simplifying gives:
u2=2gh
Therefore, the initial velocity u=√2gh.
4. Calculate the time to reach the top:
- Using the equation of motion:
v=u+at
- At the top, v=0:
0=√2gh−gsin(α)t
Rearranging gives:
t=√2ghgsin(α)
Step 2: Analyze the motion on the second inclined plane (BC)
1. Identify the parameters:
- Let the angle of inclination of plane BC be β.
- The height from which the particle slides down is the same height h.
2. Calculate the time to slide down:
- The acceleration down the incline is gsin(β).
- The distance down the incline is h/sin(β).
3. Using the equations of motion:
- The initial velocity at the top of plane BC is 0 (as it comes to rest at the top of AB).
- Using the equation:
s=ut+12at2
- Here, s=hsin(β), u=0, and a=gsin(β):
hsin(β)=0+12gsin(β)t2
Rearranging gives:
t2=2h/sin(β)gsin(β)
Therefore:
t=√2hgsin2(β)
Step 3: Calculate the total time
1. Total time:
T=tAB+tBC=√2ghgsin(α)+√2hgsin2(β)
Final Expression
Thus, the total time taken to reach point C is:
T=√2h√gsin(α)+√2hgsin2(β)
- Let the angle of inclination of plane AB be α.
- Let the height of plane AB be h.
- The initial velocity u is just sufficient to reach the top, which means at the top, the final velocity v=0.
- The motion can be analyzed using the equation:
v2=u2+2as
- Here, v=0 (at the top), a=−gsin(α) (the component of gravitational acceleration acting down the incline), and s=h/sin(α) (the distance along the incline).
0=u2−2gsin(α)⋅hsin(α)
Simplifying gives:
u2=2gh
Therefore, the initial velocity u=√2gh.
- Using the equation of motion:
v=u+at
- At the top, v=0:
0=√2gh−gsin(α)t
Rearranging gives:
t=√2ghgsin(α)
- Let the angle of inclination of plane BC be β.
- The height from which the particle slides down is the same height h.
- The acceleration down the incline is gsin(β).
- The distance down the incline is h/sin(β).
- The initial velocity at the top of plane BC is 0 (as it comes to rest at the top of AB).
- Using the equation:
s=ut+12at2
- Here, s=hsin(β), u=0, and a=gsin(β):
hsin(β)=0+12gsin(β)t2
Rearranging gives:
t2=2h/sin(β)gsin(β)
Therefore:
t=√2hgsin2(β)
T=tAB+tBC=√2ghgsin(α)+√2hgsin2(β)
Thus, the total time taken to reach point C is:
T=√2h√gsin(α)+√2hgsin2(β)
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - NCRT Exercises22videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - Additional Exercises13videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 6 Long answer (NCERT)9videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
A paricle is projected up from the bottom of an inlined plane of inclination α with velocity v0 If it returns to the points of projection after an elastic impact with the plane, find the total time of motion of the particle.
View SolutionA body is projected from the bottom of a smooth inclined place with a velocity of 20ms−1, If it is just sufficient to carry it to the top in 4s, find the inclination and height of the plane.
View Solution
Knowledge Check
- Question 1 - Select One
A particle is projected with a velocity u from the foot of an inclined plane whose inclination to the horizon is β. It strikes. the plane at right angles if
Atan(α−β)=cotβB2tan(α−β)=cotβC2cot(α−β)=cotβDNone of these - Question 2 - Select One
A particle is projected at an angle α with the horizontal from the foot of an inclined plane making an angle β with horizontal . Which of the following expressions holds good if the particle strikes the inclined plane normally?
Acotβ=−tan(α−β)Bcotβ=2tan(α−β)Ccotα=tan(α−β)Dcotα=2tan(α−β) - Question 3 - Select One
A ball is projected perpendicularly from an inclined plane of angle θ, with speed 'u' as shown. The time after which the projectile is making angle 45∘ with the inclined plane is :
 AugsinθBugcosθCug{sinθ+cosθ}Dug{sinθ−cosθ}
AugsinθBugcosθCug{sinθ+cosθ}Dug{sinθ−cosθ}
A ball is projected from the foot of an inclined plane of inclination 30∘ at an angle 60∘ with the horizontal,with velocity 20√3ms−1 .The time after which the ball will strike the plane is
View SolutionA particle is projected from the bottom of an inclined plane of inclination 30∘ with velocity of 40m/s at an angle of 60∘ with horizontal. Find the speed of the particle when its velocity vector is parallel to the plane. Take g=10m/s2.
View SolutionA particle is projected with a certain velocity at an angle α above the horizontal from the foot of an inclined plane of inclination 30∘. If the particle strikes the plane normally then α is equal to
View SolutionA particle sides down from rest on an inclined plane of angle θ with horizontal. The distances are as shown. The particle slides down to the position A, where it velocity is v.
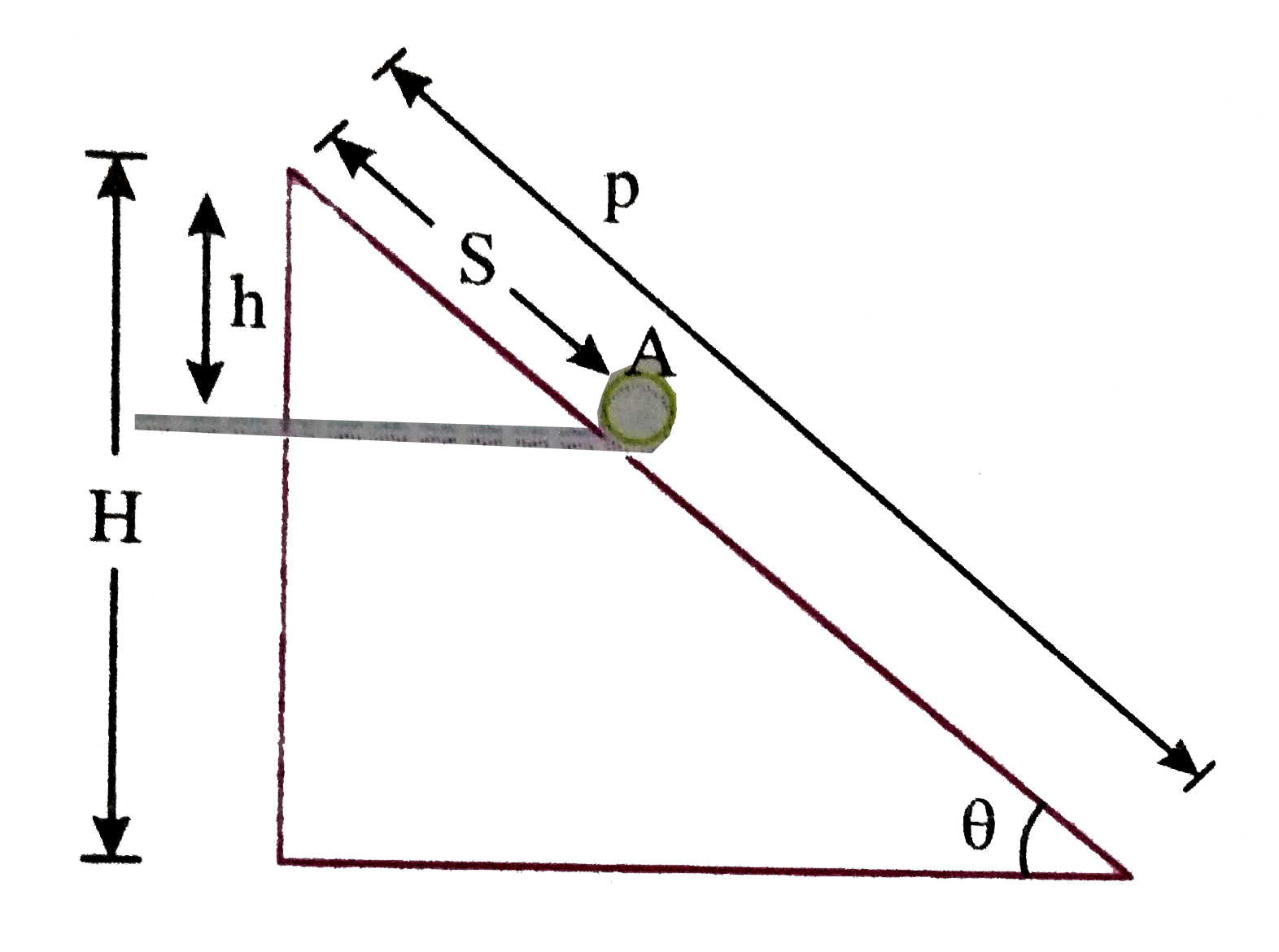 .View Solution
.View SolutionA particle is projected with a velocity of 20 m/s at an angle of 30∘ to an inclined plane of inclination 30∘ to the horizontal. The particle hits the inclined plane at an angle 30∘, during its journey. The time of flight is -
View Solution

