Question

An object $A$ is kept fixed at the point $x=3m$ and $y=1.25m$ on a plank $p$ raised above the ground . At time $t=0$ the plank starts moving along the $+x$ direction with an acceleration $1.5m/s^2$. At the same instant a stone is projected from the origin with a velocity $\overrightarrow{u}$ as shown . A stationary person on the ground observes the stone hitting the object during its downward motion at an angle $45(\circ )$ to the horizontal . All the motions are in the $X-Y$plane . Find $\overrightarrow{u}$ and the time after which the stone hits the object . Take $g=10m/s$

Explanation

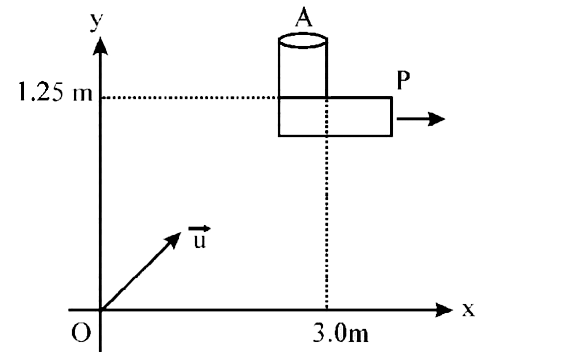
Let the stone be promected from (O) with velocity (u), making an angle ` theta` with X-axis . It hits the object ` A and at ` B` in time 9t) . It means , the object gores from ` A to B` in time 9t) . Let`vec v`be the velocity of stone at ` B. Fig. 2 (APC). 5.`
.
Taking horizontal motion from ` O to B`, here `
` OB-1 = OA_1 + A-1 B-1`
So ` u cos theta theta t = 3.0 + 1/2 xx 1. 5 t^2` ...(i)
Taking vertical motion from ` O to B`, here
` 1.25 = ( u sin theta) t 2/2 gt^2` ...(ii)
Also ` v cos 45^@ = u cos theta` ...(iii)
and `- v sin 45^2 =u theta - gt` ...9iv)
Diveding (iii) by (v) , we get
` -1= ( u cos theta0/( u sin theta- gt)` or ` u cos theta + u sin theta = gt`
or ` u ( cos theta + sin theta0 = gt` ....(v) ltBrgt ` From (ii), ( u sin theta) t = 1.25 + 1/2 gt^2` ...9iv)`
Adding (i) and (vi), we have
` ut (cos theta + sing theta )`
`=3.0 + 1/2 1.5 t^2 + 1.25 + 1/2 gt^2`
` gt^2 = 4.25 + 1/2 xx 3/2t^2 = 1/2 gt^2` [ From (v0 ]`
` 10 t^2 = 4. 25 + 0. 7 5 t^2 + 5 t^2 [ :. g= 10 ms^(-2) ]`
or 910 - 5.75 ) t^2 = 4. 25 or t^2 = 1 or t= 1 s`
Putting ` t= 1 s` in ( i) and (ii), we have
` u cos theta = 3.0 = 1/2 xx 1.5 1^2 = 3. 75` ...(vii)`
:. u^2 (cos^2 theta + sin ^2 theta ) = (3. 75(=)^2 = 9 6.25)^2`
or ` u= sqrt( (3.75)^2 + ( 6.25 )^2 ) = 7. 30 ms^-1)`
Dividing (viiii) by (vii), we have
` tan theta (6. 25) /(3.75) = 5/3 or theta tan ^(-1) ( 5/3)`.