Two bodies were thrown simultaneously from the same point , on straight up and the other, at angle θ=60∘ to the horizontal . The initial velocity of each body is equal to u=30m/s. Neglecting the air resistance, find the distance between the bodies after 2 seconds.
For first body, the distance moved in vetical upward direction in time (t0 is y=ut−12>2
For second body, the horizontal dsitance, Mbrgt x'=ucosθ×t=30×12=30m
and vertical distance, y'=usinθt−12>2
Vertical distance between two dodies after time (t),
=y−y'=(ut−12>2)−(usinθt−12>2)
=ut−usinθt
=30×3−30×(√3/20×2≈8m.
The distance between two boies after tiem (t) is
=√(y−y)2+x'2=√82+302≈31m.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 Multiple choice10videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 2 Multiple choice10videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 3 Problems for practice67videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - GRAVIATIONEXERCISE - Assertion-Reason Type Questions19videos
GRAVIATION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Assertion- Reason Type Questions17videos
LAWS OF MOTION
Similar Questions
Two bodies were thrown simultaneously from the same point, one, straight up, and the other, at an angle of θ=60∘ to the horizontal. The initial velocity of each body is equal to v0=25m/s. Neglecting the air drag, find the distance between the bodies t=1.70s later.
View SolutionTwo bodies were thrown simultaneously from the same point, one straight up, and the other at an angle of θ=30∘ to the horizontal. The initial velocity of each body is 20ms−1. Neglecting air resistance, the distance (in meter) between the bodies at t=1.2 later is
View Solution
Knowledge Check
- Question 1 - Select One
Two projectiles thrown from the same point at angles 60∘and30∘ with the horizontal attain the same height. The ratio of their initial velocities is
A1B2C√3D1√3 - Question 2 - Select One
A body is projected with velocity 60m/s at 30∘ to the horizontal.The velocity of the body after 3seconds is
A20ˆi+20√3ˆjB30ˆiC10√3ˆjD30√3ˆi - Question 3 - Select One
Two bodies are projected with the same velocity. If one is projected at an angle of 30∘ and the other at an angle of 60∘ to the horizontal, the ratio of the maximum heights reached is
A3:1B1:3C1:2D2:1
Two bodies are thrown simultaneously from the same point. One thrown straight up and the other at an angle α with the horizontal. Both the bodies have velocity equal to u. Find the separation between the bodies at time t.
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneously towards each other, one is thrown horizontally with a velocity of 8m/s and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. This horizontal distance between points A and B equal to 8m.Then find
a)The initial velocity V0 of the body thrown at an angle 45∘
b)The time of flight t of the bodies before colliding
c) The coordinate (x,y) of the point of collision (consider the bottom of the tower A as origin )is
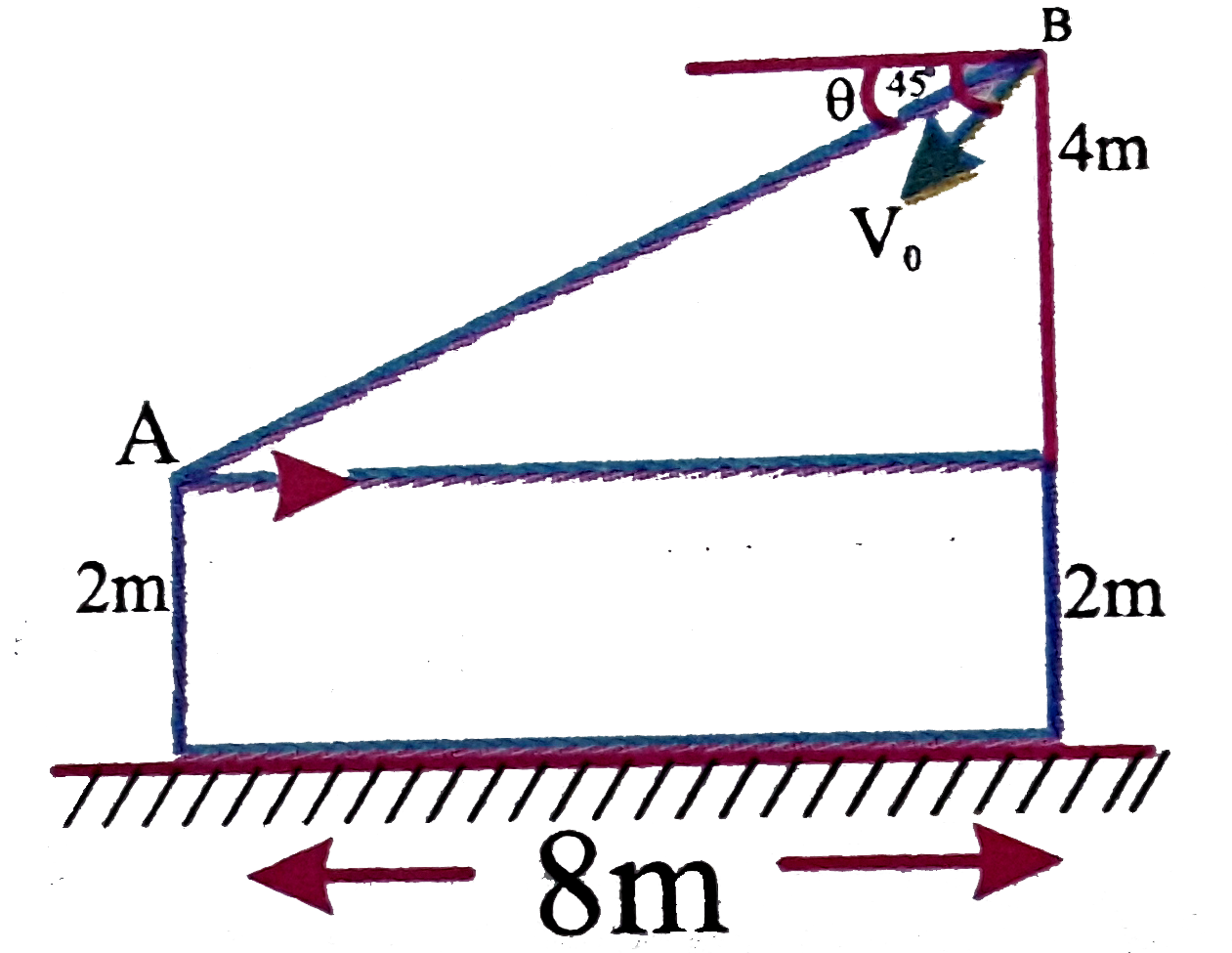 View Solution
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneouly towards each other, one is thrown horizontally with a velocity of 8ms and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. The horizontal distance between points A and B equal to 8m.Then find
The initial velocity V0 of the body thrown at an angle 45∘
The time of flight of the bodies before colliding
The coordinate (x,y) of the point of collision (consider the botton of the tower A as origin) isView SolutionTwo bodies are thrown at the same time and in opposite directions and with an equal velocity v0 at angles α1 and α2 to the horizon. What is the velocity with which the bodies move relative to each other -? What will be the distance between the bodies be after time t elapses ?
View SolutionA body is thrown horizontally from the top of a tower of height 5m. It touches the ground at a distance of 10m from the foot of the tower. Find the initial velocity of the body.
View Solution

