Two bodies were thrown simultaneously from the same point, one straight up, and the other at an angle of θ=30∘ to the horizontal. The initial velocity of each body is 20ms−1. Neglecting air resistance, the distance (in meter) between the bodies at t=1.2 later is
The correct Answer is:24
To solve the problem of finding the distance between two bodies thrown simultaneously, we can follow these steps:
Step 1: Analyze the motion of the first body
The first body is thrown straight up with an initial velocity of u1=20m/s. Since it is thrown vertically, its initial velocity vector can be expressed as:
u1=0^i+20^j
Step 2: Analyze the motion of the second body
The second body is thrown at an angle of θ=30∘ with the same initial velocity of u2=20m/s. We can resolve this velocity into its horizontal and vertical components:
u2x=20cos(30∘)=20⋅√32=10√3m/s
u2y=20sin(30∘)=20⋅12=10m/s
Thus, the initial velocity vector for the second body is:
u2=10√3^i+10^j
Step 3: Determine the relative acceleration
Both bodies are subject to the same gravitational acceleration acting downward, which is a=0^i−g^j where g≈9.81m/s2. Since both bodies experience the same acceleration, the relative acceleration between them is:
a12=a1−a2=0
Step 4: Calculate the relative velocity
The relative velocity between the two bodies can be calculated as:
u12=u1−u2=(0^i+20^j)−(10√3^i+10^j)
This simplifies to:
u12=−10√3^i+10^j
Step 5: Calculate the magnitude of the relative velocity
The magnitude of the relative velocity is given by:
|u12|=√(−10√3)2+(10)2=√300+100=√400=20m/s
Step 6: Calculate the distance between the bodies after t=1.2s
Since the relative acceleration is zero, the distance between the two bodies after time t can be calculated using:
Distance=|u12|⋅t
Substituting the values:
Distance=20m/s⋅1.2s=24m
Final Answer
The distance between the two bodies after t=1.2s is 24m.
---
The first body is thrown straight up with an initial velocity of u1=20m/s. Since it is thrown vertically, its initial velocity vector can be expressed as:
u1=0^i+20^j
The second body is thrown at an angle of θ=30∘ with the same initial velocity of u2=20m/s. We can resolve this velocity into its horizontal and vertical components:
u2x=20cos(30∘)=20⋅√32=10√3m/s
u2y=20sin(30∘)=20⋅12=10m/s
Thus, the initial velocity vector for the second body is:
u2=10√3^i+10^j
Both bodies are subject to the same gravitational acceleration acting downward, which is a=0^i−g^j where g≈9.81m/s2. Since both bodies experience the same acceleration, the relative acceleration between them is:
a12=a1−a2=0
The relative velocity between the two bodies can be calculated as:
u12=u1−u2=(0^i+20^j)−(10√3^i+10^j)
This simplifies to:
u12=−10√3^i+10^j
The magnitude of the relative velocity is given by:
|u12|=√(−10√3)2+(10)2=√300+100=√400=20m/s
Since the relative acceleration is zero, the distance between the two bodies after time t can be calculated using:
Distance=|u12|⋅t
Substituting the values:
Distance=20m/s⋅1.2s=24m
The distance between the two bodies after t=1.2s is 24m.
Topper's Solved these Questions
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 More Than One Correct
8 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- PROJECTILE MOTIONBOOK - DC PANDEYCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 1 Subjective
21 Videos
- MOTION IN A PLANEBOOK - DC PANDEYCHAPTER - MOTION IN A PLANEEXERCISE - (C )Medical entrances gallery
32 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEYCHAPTER - PROPERTIES OF MATTEREXERCISE - Integer
8 Videos
Similar Questions
Two bodies were thrown simultaneously from the same point, one, straight up, and the other, at an angle of θ=60∘ to the horizontal. The initial velocity of each body is equal to v0=25m/s. Neglecting the air drag, find the distance between the bodies t=1.70s later.
View SolutionTwo bodies were thrown simultaneously from the same point , on straight up and the other, at angle θ=60∘ to the horizontal . The initial velocity of each body is equal to u=30m/s. Neglecting the air resistance, find the distance between the bodies after 2 seconds.
View Solution
Knowledge Check
Two bodies are projected with the same velocity. If one is projected at an angle of 30∘ and the other at an angle of 60∘ to the horizontal, the ratio of the maximum heights reached is
A3:1B1:3C1:2D2:1Two bodies are thrown with the same initial velocity at angles θ and (90∘−θ) respectively with the horizontal, then their maximum height are in the ratio
A1 : 1Bsinθ:cosθCsin2θ:cos2θDcosθ:sinθTwo bodies are thrown simultaneously from a tower with same initial velocity v0: one vertically upwards, the other vertically downwards. The distance between the two bodies after time t is
A2v0t+12>2B2v0tCv0t+12g t2Dv0t
Two bodies are thrown simultaneously from the same point. One thrown straight up and the other at an angle α with the horizontal. Both the bodies have velocity equal to u. Find the separation between the bodies at time t.
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneously towards each other, one is thrown horizontally with a velocity of 8m/s and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. This horizontal distance between points A and B equal to 8m.Then find
a)The initial velocity V0 of the body thrown at an angle 45∘
b)The time of flight t of the bodies before colliding
c) The coordinate (x,y) of the point of collision (consider the bottom of the tower A as origin )is
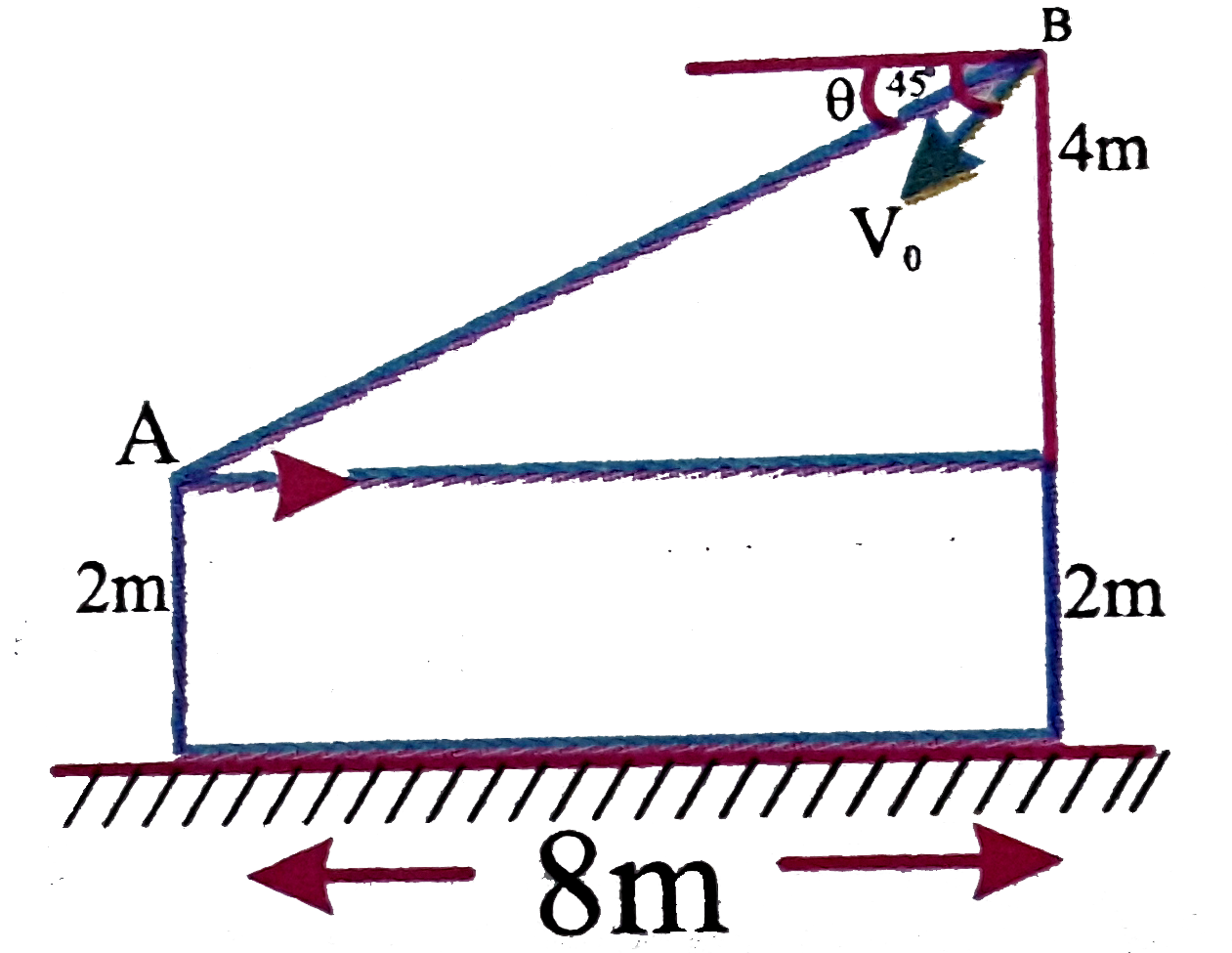
View SolutionFrom points A and B, at the respective heights of 2m and 6m, two bodies are thrown simultaneouly towards each other, one is thrown horizontally with a velocity of 8ms and the other, downward at an angle 45∘ to the horizontal at an initial velocity v0 such that the bodies collide in flight. The horizontal distance between points A and B equal to 8m.Then find
The initial velocity V0 of the body thrown at an angle 45∘
The time of flight of the bodies before colliding
The coordinate (x,y) of the point of collision (consider the botton of the tower A as origin) is
View SolutionA body is thrown horizontally from the top of a tower of height 5m. It touches the ground at a distance of 10 m from the foot of the tower. The initial velcotiy (in m/s) of the body is (g=10ms−2)
View SolutionTwo bodies are thrown at the same time and in opposite directions and with an equal velocity v0 at angles α1 and α2 to the horizon. What is the velocity with which the bodies move relative to each other -? What will be the distance between the bodies be after time t elapses ?
View Solution
