The resultant of two vectors →P and →Q is →R. If the magnitude of →Q is doubled, the new resultant vector becomes perpendicular to →P. Then, the magnitude of →R is equal to

A

P+Q

B

Q

C

P

D

P+Q2

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:B

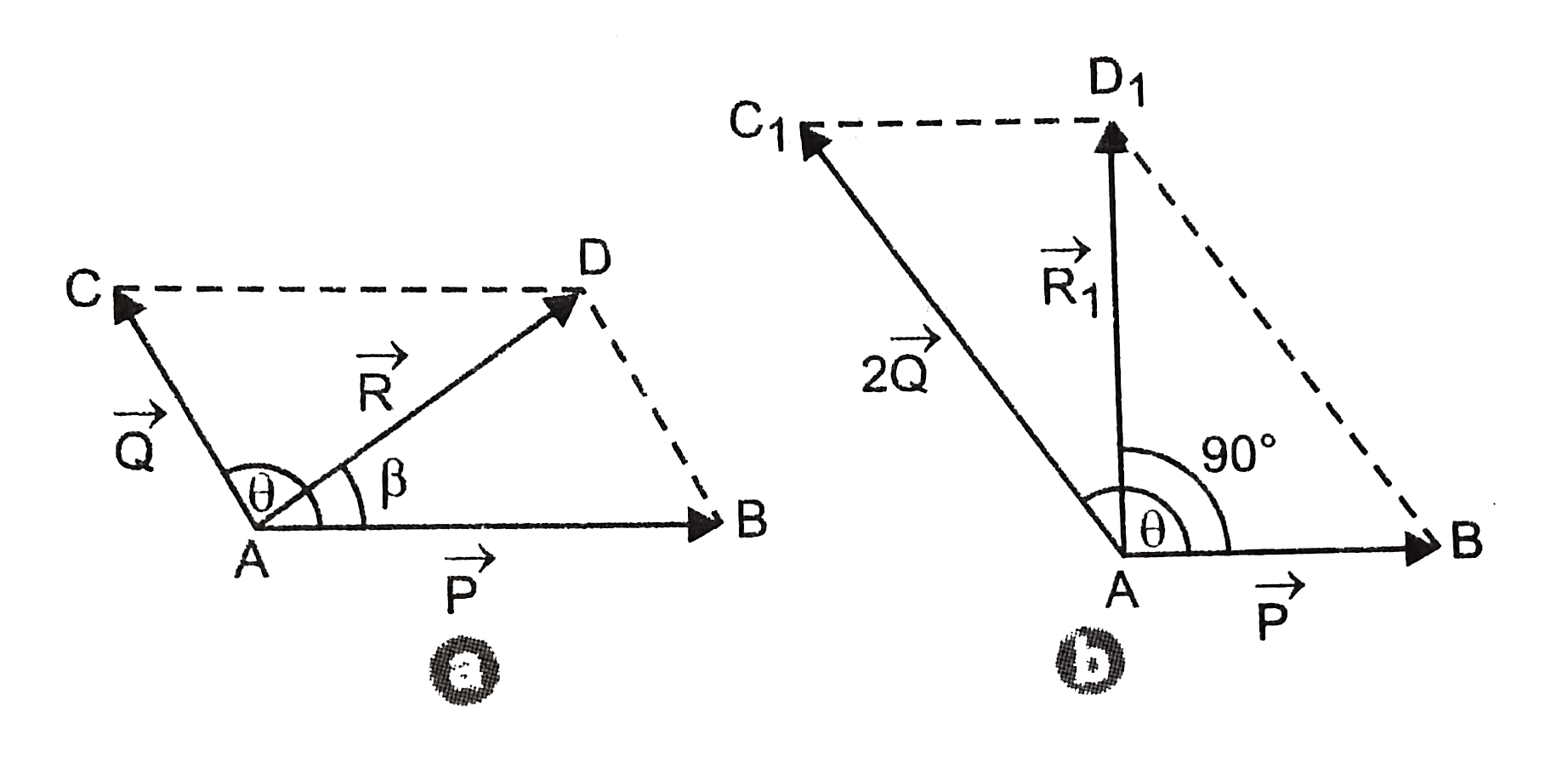ocr_image.
tanβ=QsinθP+Qcosθand
R2=P2+QPQcosθ ….(i)
When (Q)isdoub≤d,restant––––– vec R_1isperpendica––r→ vec P.Fig.2(CF).51(b).The<br> R_1^2 = P^2 + 4 Q^2 + 4 PQ cos thea....(ii)<br>Fromright∠d△ BAD_1,wehave<br> R-1^2 = ( 2 Q)^2 - P^2 = 4 Q^2 -P^2<br>Pu∈gthisvalue∈(ii),we≥t<br> Q^@ + 2 - P^2 =P^2 + 4 Q^2 + 4 PQ cos theta<bR>or P^2 + 2 PQ cos theta =0<br>Pu∈gthisvalue∈(ui),we≥t<br> R^2 = (P^2 +2 PQ cos theta =0<br>Pu∈gthisvalue∈(i),we≥t.<br> R^1 = (P^2 + 2 PQ cos theta) + Q^2 =0 + Q^2 =Q^2 or R=Q.

Updated on:21/07/2023
|
Class 11PHYSICSRECTILINEAR MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The resultant of two vectors →P and →Q is →R. If →Q is doubled then the new resultant vector is perpendicular to →P. Then magnitude of →R is :-

    AP2−Q22PQ
    BQ
    CPQ
    DP+QP−Q

  • The resultant →Pand→Q is perpendicular to →P. What is the angle between →Pand→Q?

    Acos−1(P/Q)
    Bcos−1(−P/Q)
    Csin−1(P/Q)
    Dsin−1(−P/Q)

  • if →P×→R=→Q×→R, then

    A→P=→Q
    B→P and →Q need not be equal
    CThere are infinite number of possibilities for →P (If →Q and →R are given ) which satisfy this relationship.
    D→p and →Q must be coplanar