The strings of a parachute can bear a maximum tension of wt . By what minimum acceleration can a person of 90 kg descend by means of this parachute ?
The correct Answer is: .
Here,
.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - JEE (Main and Advanced)/ Medical Entrance Special
93 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Integer Type Questions
7 Videos
- LAWS OF MOTIONBOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Fill in the blanks
20 Videos
- KINEMATICSBOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension
4 Videos
- MATHEMATICAL TOOLSBOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks
5 Videos
Similar Questions
The strings of a parachute can bear a maximum tension of 72 kg wt. By what minimum acceleration can a person of 96 kg descend by means of this parachute?
View SolutionA string tied on a roof can bear a maximum tension of 50 kg wt. The minimum acceleration that can be acquired by a man of 98 kg to descend will be [Take g=9.8m/s2]
View Solution
Knowledge Check
A string tied on a roof can bear a maximum tension of 50 kg wt. The minimum acceleration that can be acquired by a man of 98 kg to descend will be [take g = 9⋅8ms2]
A9⋅8ms2B4⋅9ms2C4⋅8ms2D5ms2A 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
A4.00ms−2B3.92ms−2C3.52ms−2D3.00ms−2One end of a massless rope, which passes over a massless and frictionless pulley P is tied to a hook C while the other end is free. Maximum tension that the rope can bear is 360 N. With what value of maximum safe acceleration (in ms−2) can a man of 60kg climb down the rope?
 A(a) 16B(b) 6C(c) 4D(d) 8
A(a) 16B(b) 6C(c) 4D(d) 8
A 70 kg man in sea is being lifted by a helicopter with the help of a rope , which can bear a maximum tension of 100 kg wt . With what maximum acceleration the helicopter should rise so that the rope does not break ? Take g=9.8m/s2 .
View SolutionA 50 kg man stuck in flood is being lifted vertically by an army helicopter with the help of light rope which can bear a maximum tension of 70 kg-wt. The maximum acceleration with which helicopter can rise so that rope does not breaks is (g=9.8ms−2)
View SolutionA stone of mass 4 kg is attached to a string of 10 m length and is whirled in a horizontal circle. The string can withstand a maximum tension of 160 N. Calculate the maximum velocity of revolution that can be given to the stone without breaking the string.
View SolutionA monkey of mass 30 kg climbs a rope which can withstand a maximum tension of 360 N. The maximum acceleration which this rope can tolerate for the climbing of monkey is:
(g=10m/s2)
View SolutionOne end of a massless rope, which passes over a massless and frictionless pulley P is tied to fixed hook C, while the other end is free. Maximum tension that the rope can bear is 960 N. With what value of max. safe acceleration (m/s2) can a man of 60 kg climb on the rope?
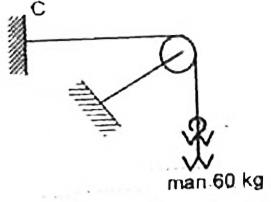
View Solution
