A body of mass m is released from the top of a rough inclined plane of length l and height h If f is the force of friction prove that the body will reach the bottom with a velocity υ=√2m(mgh−fl) .
On reaching the battom loss in P.E = mgh
Gain in K.E=12mυ2 and
work done against friction f×l
According to the law of conservation of energy
12mυ2+f×l=mgh
υ=√2m(mgh−f×l)
which was to be proved.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - JEE (Main and Advanced)/ Medical Entrance Special93videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Integer Type Questions7videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - LAWS OF MOTIONEXERCISE - Fill in the blanks20videos
LAWS OF MOTION
- BOOK - PRADEEPCHAPTER - KINEMATICSEXERCISE - 1 NCERT Comprehension4videos
KINEMATICS
- BOOK - PRADEEPCHAPTER - MATHEMATICAL TOOLSEXERCISE - Fill in the blanks5videos
MATHEMATICAL TOOLS
Similar Questions
A body of mass m is released from the top of a rough inclined plane as shown in figure. If the frictional force be F, then body will reach the bottom with a velocity
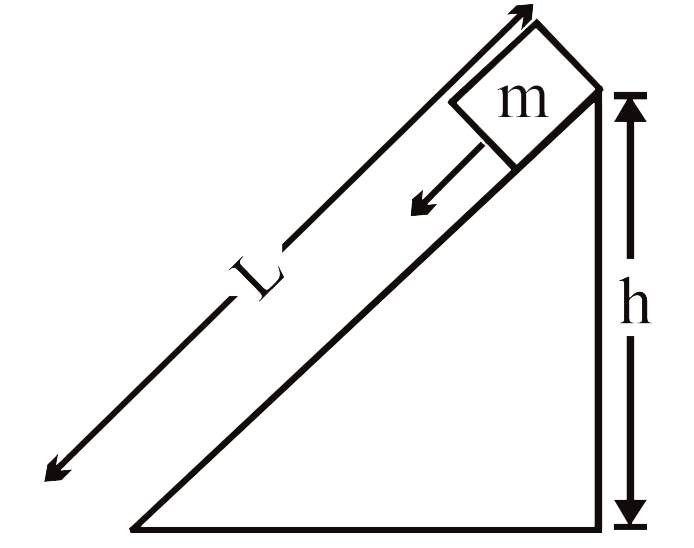 View Solution
View SolutionIf the body starts from rest from the top of the rough inclined plane of length 1, time taken to reach the bottom of the plane is
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is released from the top of a mooth inclined plane of height h its speed at the bottom of the plane is proportion to
Am0BmCm2Dm−1 - Question 2 - Select One
An object of mass m is released from rest from the top of a smooth inclined plane of height h. Its speed at the bottom of the plane is proportional to
Am0BmCm2Dm−1 - Question 3 - Select One
A body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
AgsinαBμcosαCg(sinα−μcosα)Dg(cosα−μsinα)
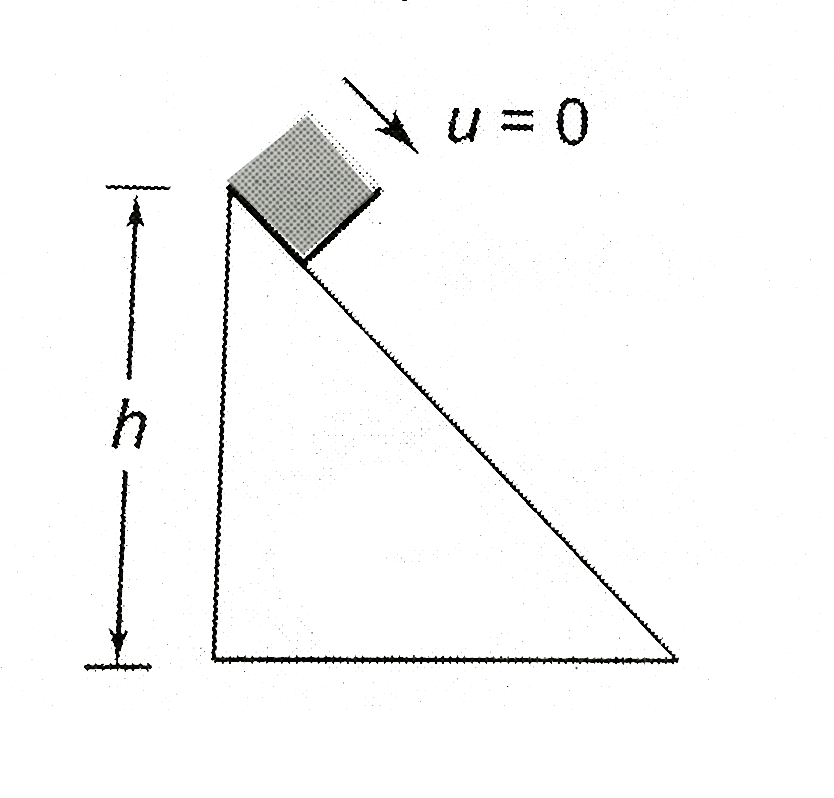
A block is released from the top of the smooth inclined plane of height h. Find the speed of the block as it reaches the bottom of the plane.View SolutionA body of mass m slides down a rough plane of inclination α . If μ is the coefficient of friction, then acceleration of the body will be
View SolutionA body is relased from the top of a building of height 19.6 m. Find the velocity with which the body hits the ground .
View SolutionA block of mass 4kg is released from the top of a rough inclines plane of height 10m. If velocity of the block is10ms at the bottom of the inclined then work done by the friction force on the block will be
View SolutionA body is allowed to slide from the top along a smooth inclined plane of length 5m at an angle of inclination 30∘.If g=10ms−2, time taken by the body to reach the bottom of the plane is
View Solution

