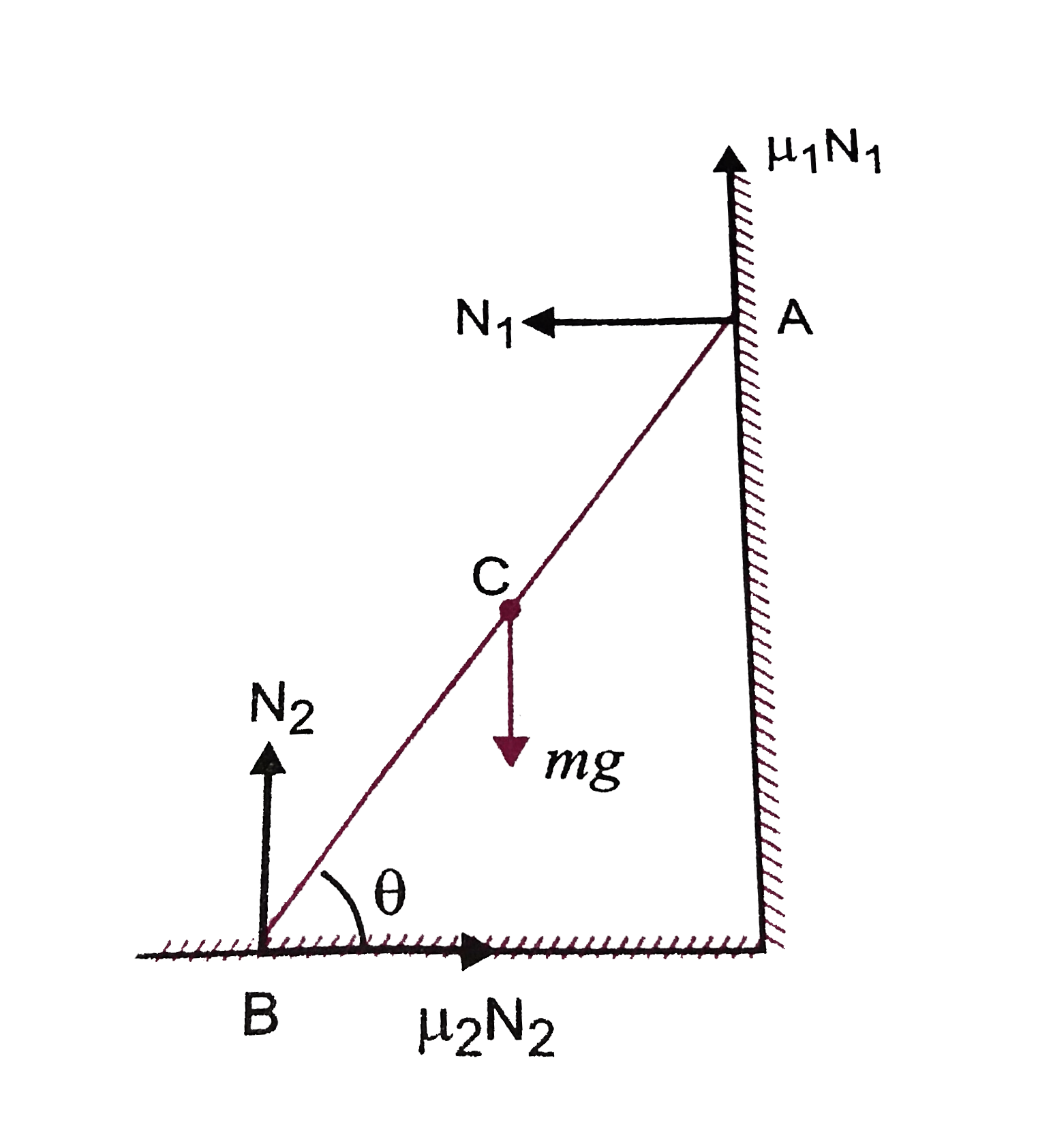
In the figure, a ladder of mass m is shown leaning against a wall. It is in static equilibrium making an angle $θ$ with the horizontal floor. The coefficient of friction between the wall and the ladder is $μ_{1}$ and that between the floor and the ladder is $μ_{2} .$ the normal reaction of the wall on the ladder is $N_{1}$ and that of the floor is $N_{2} .$ if the ladder is about to slip. than

$μ_{1} = 0, μ_{2} \neq 0 and N_{2} tan θ = m g / 2$

$μ_{1} \neq 0, μ_{2} = 0 and N_{1} tan θ = m g / 2$

$μ_{1} = 0, μ_{2} \neq 0 and N_{2} = \frac{m g}{1 + μ_{1} μ_{2}}$

$μ_{1} = 0, μ_{2} \neq 0 and N_{1} tan θ = \frac{m g}{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:c,d

Updated on:21/07/2023

A ladder of length $l$ and mass $m$ is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is $μ$ . The angle $θ$ at which the ladder will stay in equilibrium is
A $θ = {tan}^{- 1} (μ)$
B $θ = {tan}^{- 1} (2 μ)$
C $θ = {tan}^{- 1} (\frac{μ}{2})$
Dnone of these
A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is

A50N
B $50 \sqrt{3} N$
C $\frac{60}{\sqrt{3}} N$
D100N
A ladder $5 m$ long rests against a vertical wall. If its top slides down at the rate of $10 c m / sec$ , then, when the foot of the ladder is $4 m$ away from the wall, the angle between the floor and the ladder is decreasing at the rate of
A $\frac{π}{4} radians / sec$ .
B $\frac{4}{π} radians / sec$ .
C $(0.025) radians / sec$ .
D $\frac{π}{6} radians / sec$ .