Two discs of radii $R and 2 R$ are pressed against eachother. Initially, disc wit radius $R$ is rotating with angular velocity $ω$ and other disc is stationary. Both discs are hinged at their respective centres and are free to rotate about them. Moment of inertiaof smaller disc is $I$ and of bigger disc is $2 I$ about their respective axis of rotation. Find the angular velocity of bigger disc after long time.

Video Solution

Text Solution

Verified by Experts

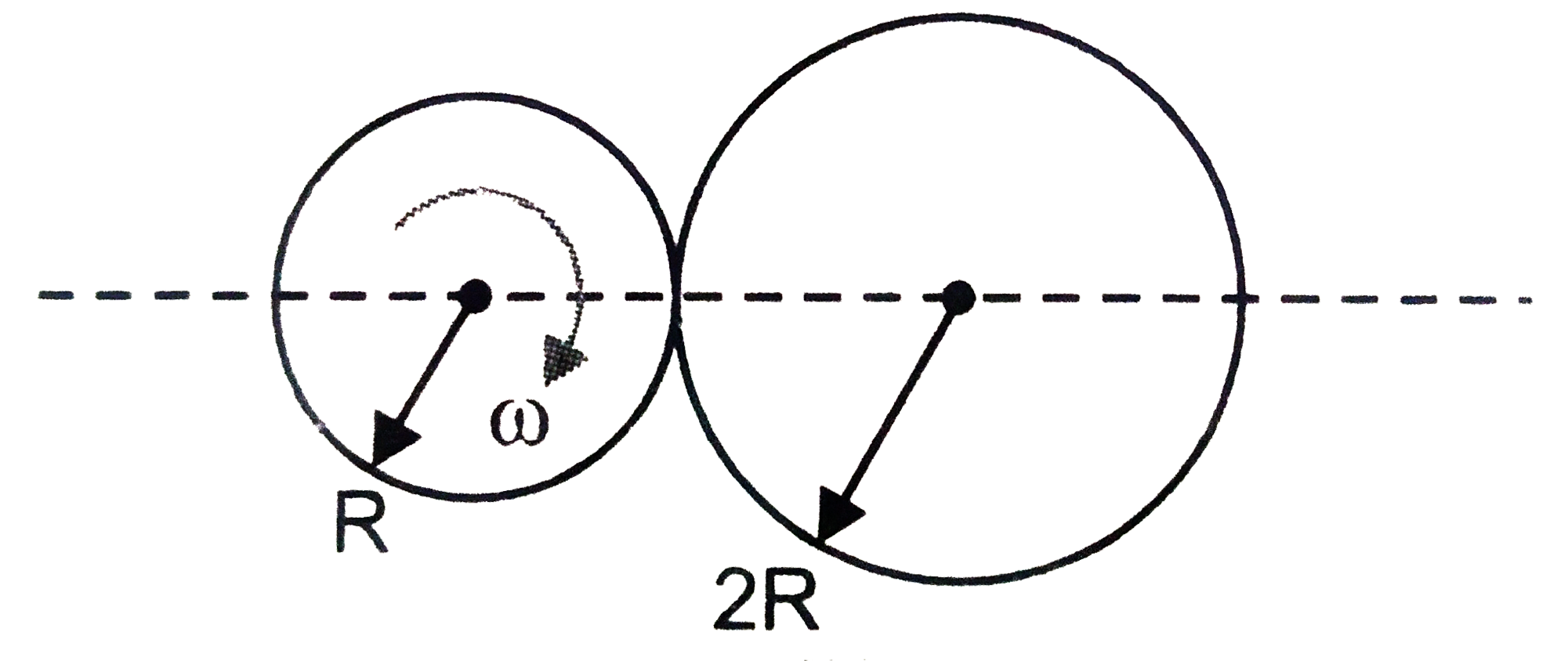
As the discs are pressed against eachother, an equal and opposite frictional force will act on both the discs, till the time rolling starts and hence the linear speed of the circumference of the two discs becomes the same.
Let $ω_{1} =$ angular velocity of smaller disc after long time $t$
$ω_{2} =$ angular velocity of bigger disc after long time $t$
$f =$ force of friction between the two discs when rolling starts,
$υ_{1} = υ_{2}$
$ω_{1} R = ω_{2} (2 R) ∴ ω_{1} = 2 ω_{2}$
For smaller disc, $τ = f \times R = \frac{I (ω - ω_{1})}{t}$ ..(i)
For bigger disc, $τ_{2} = f \times 2 R = \frac{2 I (ω_{2} - 0)}{t}$
or $f \times R = \frac{I ω_{2}}{t}$ ..(ii)
From (i) and (ii), $ω - ω_{1} = ω_{2}$
or $ω - 2 ω_{2} = ω_{2}$
$ω = 2 ω_{2}$
or $ω = ω / 3$

Updated on:21/07/2023

A disc of mass $m$ has a charge $Q$ distributed on its surface. It is rotating about an $X X'$ with a angular velocity $ω$ . The force acting on the disc is

Azero
B $ω R B / π$
C $2 Q ω B R$
Dnone of these
A circular disc is rotating about its own axis at uniform rate completes $30$ rotations in one minute.The angular velocity of disc in rad $s^{- 1}$ is
A $2 π$
B $π$
C $\frac{π}{2}$
D $\frac{π}{4} i$
A heavy disc is rotating with uniform angular velocity $ω$ about its own axis. A piece of wax sticks to it. The angular velocity of the disc will
Aincrease
Bdecrease
Cbecomes zero
Dremain unchanged