
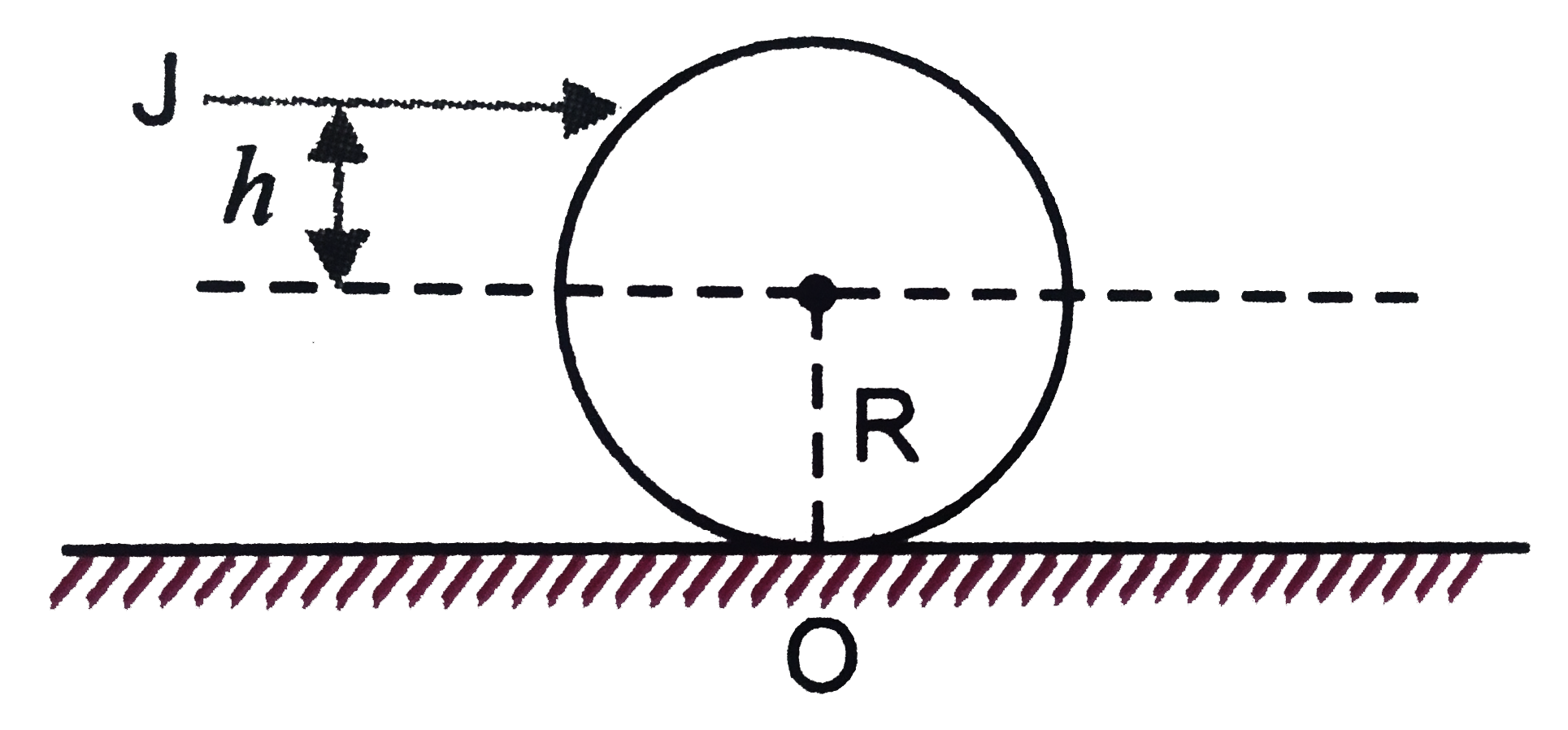
A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its backward slipping eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.
If we represent the impulse given to the ball by J, then the initial velocity is
υcm=υ0=JM ..(i)
and ω=LI=Mυ0×h25MR2=5υ0h2R2 ..(ii)
After the application o fimpulse, angular momentum of the ball about O will be conserved.
i.e., Linitial=Lfinal
Icmω+Mυ0×R=IcmυR+Mυ×R
As υ=97υ0
∴25MR2(5υ0h2R2)+MυoR
=(25MR2R+MR)97υ0
Mh+MR=95MR
Mh=95MR−MR=45MR
h=45R
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT21videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ADDITIONAL EXERCISES11videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE E1videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions

A billiard ball, initially at rest, is given a sharp impulse by a cue. The cue is held horizontally a distance h above the centre line as shown in figure. The ball leaves the cue with a speed v0 and because of its forward english (backward slipping) eventually acquires a final
speed 97v0 show that h=45R
Where R is the radius of the ball.View SolutionThe cue stick hits a cue ball horizontally a distance x above the centre of the ball. Find the value of x for which the cue ball will instantaneously roll without slipping. Calculate the answer in terms of the radius R of the ball.
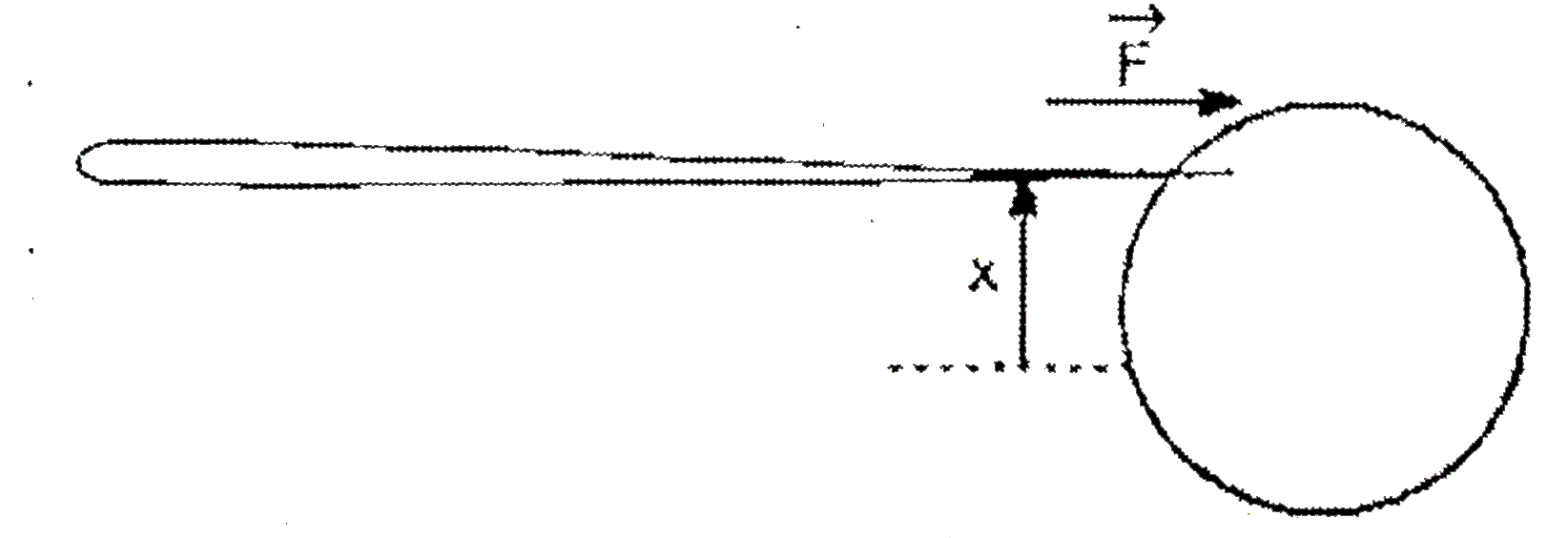 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A billiard ball of mass m and radius 7, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity Wo acquired by the ball is
A5v0r22hB2v0r25hC2v0h5r2D5v0h2r2 - Question 2 - Select One
A solid shperical ball of mass m and radius R is present on a rough horizontal surface. A person hit the ball at distance h above the centre of the ball as shown in the figure. Find out the h such that the ball starts pure rolling just after impact.
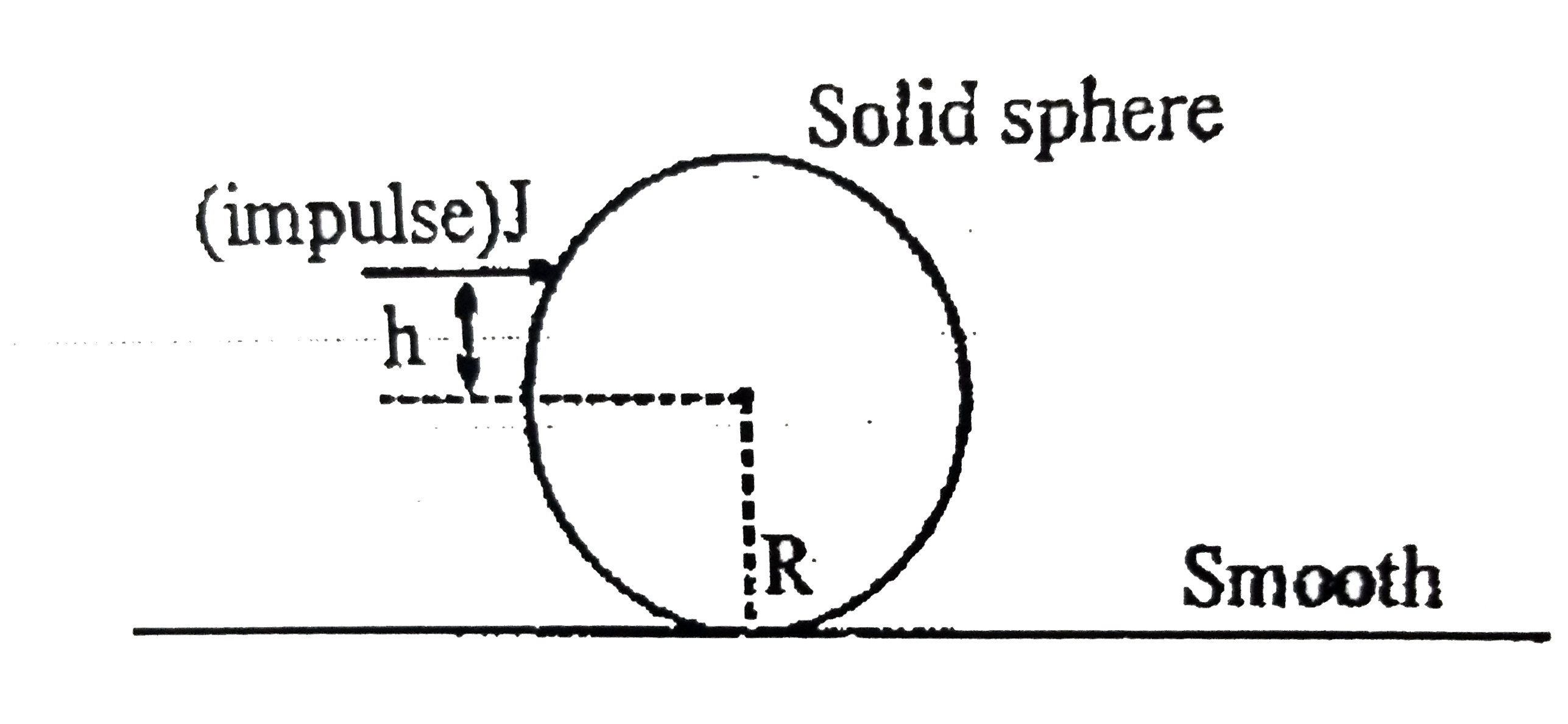 Ah=R5Bh=3R5Ch=RDh=2R5
Ah=R5Bh=3R5Ch=RDh=2R5 - Question 3 - Select One
Five balls are placed one after the other along a straight line as shown in the figure. Initially, all the balls are at rest. Then the second ball has been projected with speed v0 towards the third ball. Mark the correct statements, (Assume all collisions to be head-on and elastic.)
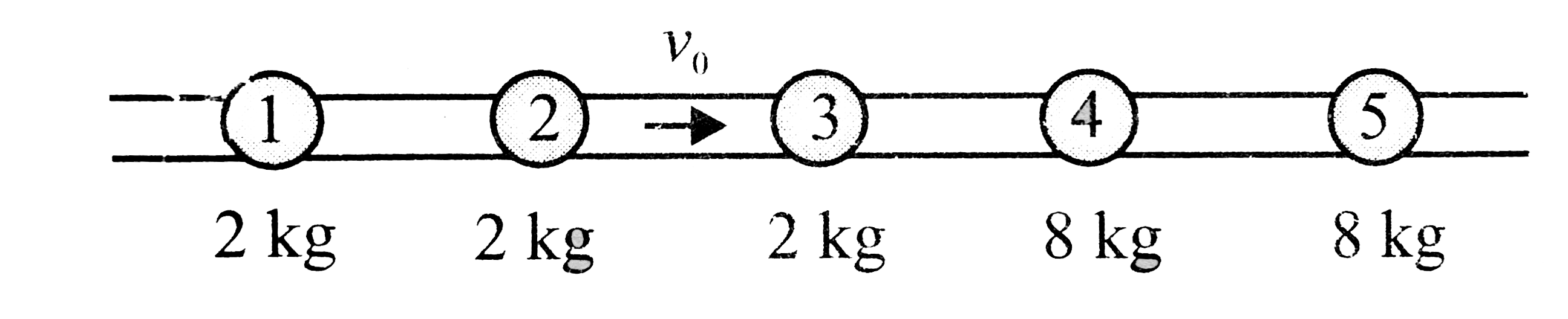 ATotal number of collisions in the process is 5BVelocity of separation between the first and fifth ball after the last possible collision is v0CFinally, three balls remain stationary.DAll of the above
ATotal number of collisions in the process is 5BVelocity of separation between the first and fifth ball after the last possible collision is v0CFinally, three balls remain stationary.DAll of the above
A billiard ball of mass m and radius r, when hit in a horizontal direction by a cue at a height h above its centre, acquired a linear velocity v0. The angular velocity ω0 acquired by the ball is
View SolutionA billiard ball is struck by a cue. The line of action of the applied impulse is horizontal andpasses through thecentre of theball. The initial velocityofthe ball is v0. If is the radius, M is the mass of the ball and μ is the coefficient of friction between the ball and the floor, find how far the ball moves before it ceases to slip on the floor.
View SolutionA particle of mass m moving horizontal with v0 strikes a smooth wedge of mass M, as shown in figure. After collision, the ball starts moving up the inclined face of the wedge and rises to a height h.
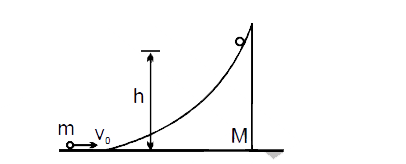
The final velocity of the wedgev2 isView SolutionConsider an idealized case of rolling of a solid ball in which the point P does not rotate in a vertical plane. But it rotates on circular path PQRSTP when observed from the centre of the ball. The radius of circular path PQRSTP is half the radius of the ball. The ball rolls without sliding with its centre moving with speed v0 in direction perpendicular to the plane of the figure calculate the kinetic energy of the rolling ball. Mass of the ball and its radius are M and R respectively.
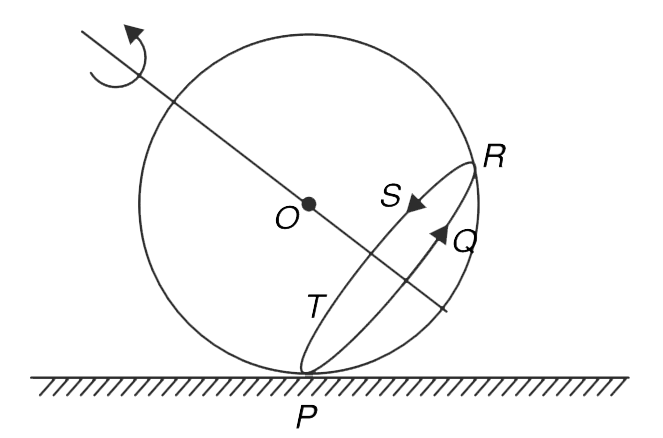 View Solution
View SolutionA solid spherical ball of radius R collides with a rough horizontal surface as shown in figure. At the time of collision its velocity is v0 at an angle θ to the horizontal and angular velocity ω0 as shown . After collision, the angular velocity of ball may
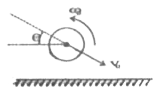 View Solution
View Solution

