Prove the result that the velocity $v$ of translation of a rolling body (like a ring, disc, cylinder or sphere) at the bottom of an inclied plane of a hight h is given by $v^{2} = \frac{2 g h}{(1 + k^{2} / R^{2})}$ using dynamical consideration (i.e. by consideration of forces and torque). Note k i sthe radius of gyration of the body about its symmentry axis, and $R$ is the radius of the body. The body starts from rest at the top of the plane.

Video Solution

Text Solution

Verified by Experts

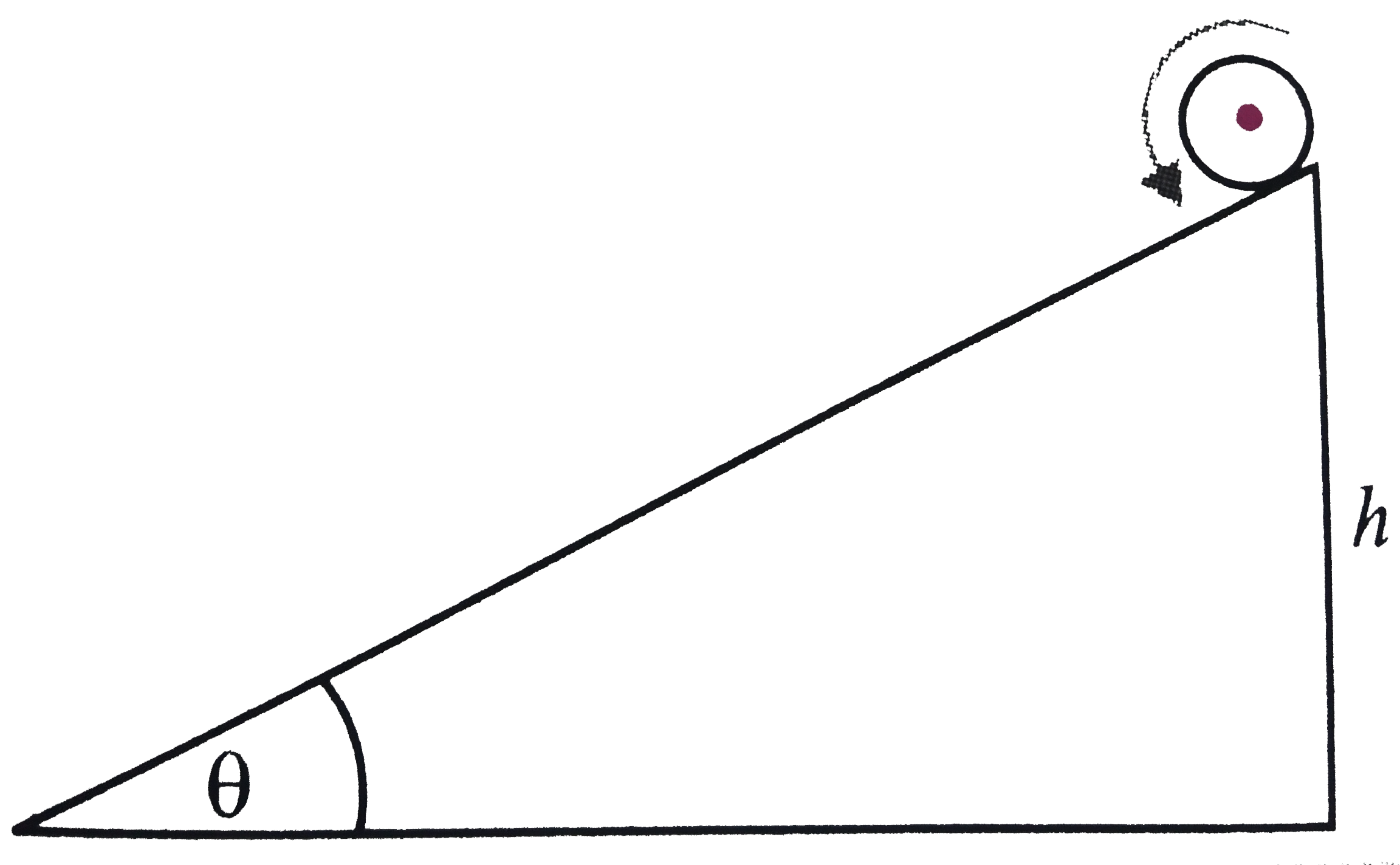
When a body rolls down an incline of hight h, we apply the principle of conservation of energy. $K . E .$ of translation $+ K . E .$ of rotation (at the bottom) $= P . E .$ at the top, Fig.
i.e. $\frac{1}{2} m v^{2} + \frac{1}{2} I ω^{2} = m g h$
$\frac{1}{2} m v^{2} + \frac{1}{2} (m k^{2}) ω^{2} = m g h$
As $ω = \frac{v}{R} ∴ \frac{1}{2} m v^{2} + \frac{1}{2} m \frac{k^{2}}{R^{2}} v^{2} = m g h$
or $\frac{1}{2} m v^{2} (1 + \frac{k^{2}}{R^{2}}) = m g h$
$v^{2} = \frac{2 g h}{(1 + k^{2} / R^{2})}$ which was to be proved.

Updated on:21/07/2023

The radius of gyration of a sphere of radius $R$ about a tangent is.
A $\frac{\sqrt{2}}{3} R$
B $\frac{\sqrt{2}}{5} R$
C $\sqrt{\frac{5}{3}} R$
D $\sqrt{\frac{7}{5}} R$
The radius of gyration of a solid sphere of radius R about its tangential is
A $\sqrt{\frac{7}{5}} R$
B $\sqrt{\frac{2}{5}} R$
C $\sqrt{\frac{5}{7}}$
D $R$
The radius of of disc is 2 m the radius of gyration of disc about an axis passing through its diameter is
A2 m
B2 cm
C1 m
D0.2 m