A disc roating about its axis with angular speed ω0 is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A,BandC on the disc shown in Fig. Will the disc roll in the direction indicated ?
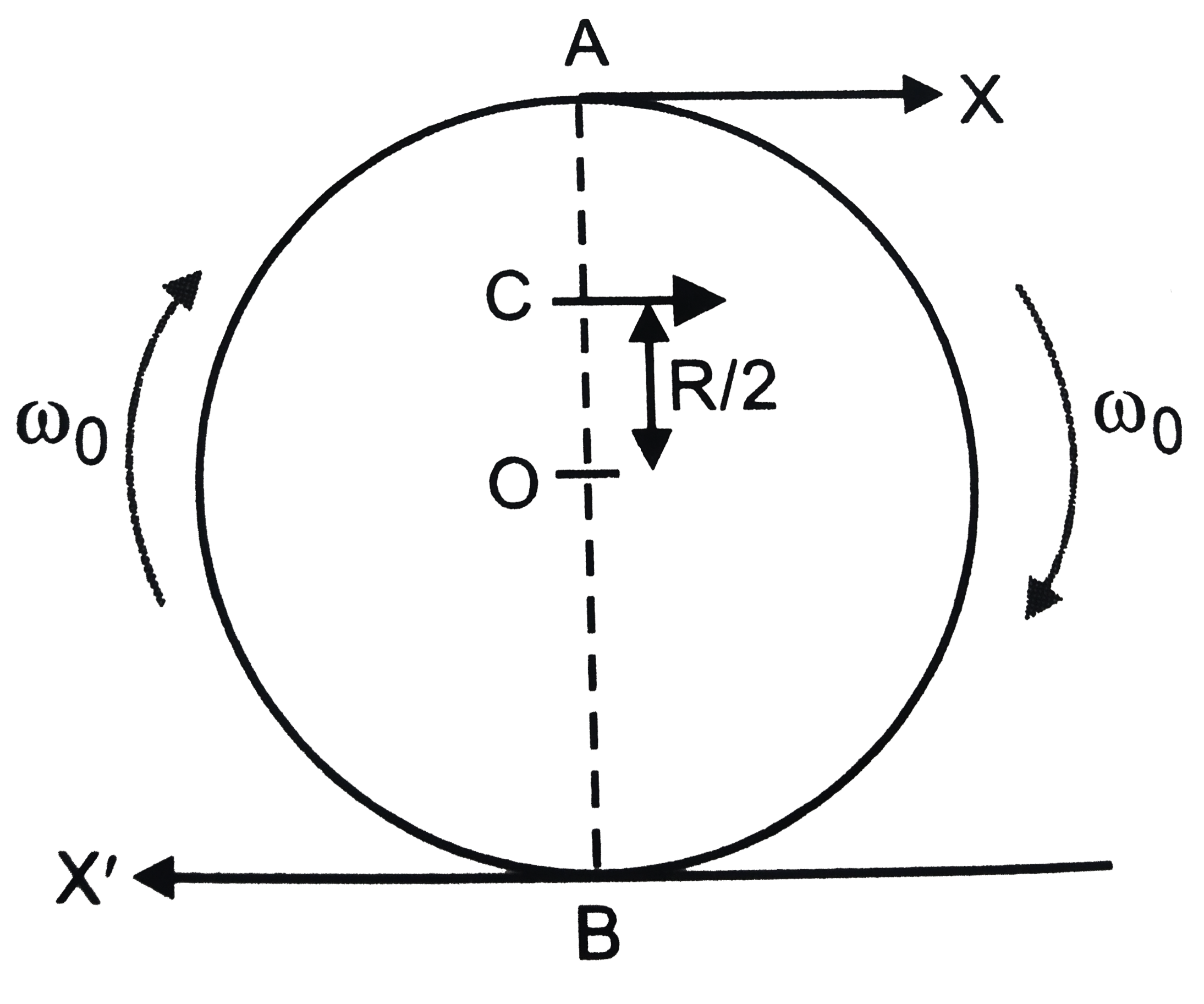
Using the relation v=rω, we get
For point A,vA=Rω0, along AX
For point B,vB=Rω0, along bX'
For point C,vc=(R2)ω0 parallel to AX,
The disc will not rotate, because it is placed on a perfectly frictionless table. without friction, rolling is not possible.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - QUESTIONS15videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - VALUE BASED QUESTIONS5videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - NCERT21videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A disc rotating about its axis with angular speed ω0 is placed lightly (without any translational pull) on a perfectly frictionless table. The radius of the disc is R. What are the linear velocities of the points A,BandC on the disc shown in Fig. Will the disc roll in the direction indicated ?
 View Solution
View SolutionA disc rotating about its axis with angular speed ω0 is placed lightly (without any translational push) on a perfectly frictionless table. The radius of the disc is R. What are on the disc shown . Will the disc roll in the direction indicated?
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A disc of radius R rolls without slipping at speed v along positive x-axis. Velocity of point P at the instant shown in Fig. is
 A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj
A→VP=(v+vrsinθR)ˆi+vrcosθRˆjB→VP=(v+vrsinθR)ˆi−vrcosθRˆjC→VP=vrsinθRˆi+vrcosθRˆjD→VP=vrsiθRˆi−vrcosθRˆj - Question 2 - Select One
A disc is rotated about its axis with a certain angular velocity and lowered gently on a rough inclined plane as shown in Fig., then
 AIt will rotate at the position where it was placed and then will move downwardsBIt will go downwards just after it is loweredCIt will go downwards first and then climb upDIt will climb upwards and then move downwards
AIt will rotate at the position where it was placed and then will move downwardsBIt will go downwards just after it is loweredCIt will go downwards first and then climb upDIt will climb upwards and then move downwards - Question 3 - Select One
A circular disc is rotating without friction about its natural axis with an angular velocity ω. Another circular disc of same material and thickness but half the raduis is gently placed over it coaxially. The angular velocity of composite disc will be
A4ω3B8ω9C7ω8D16ω17
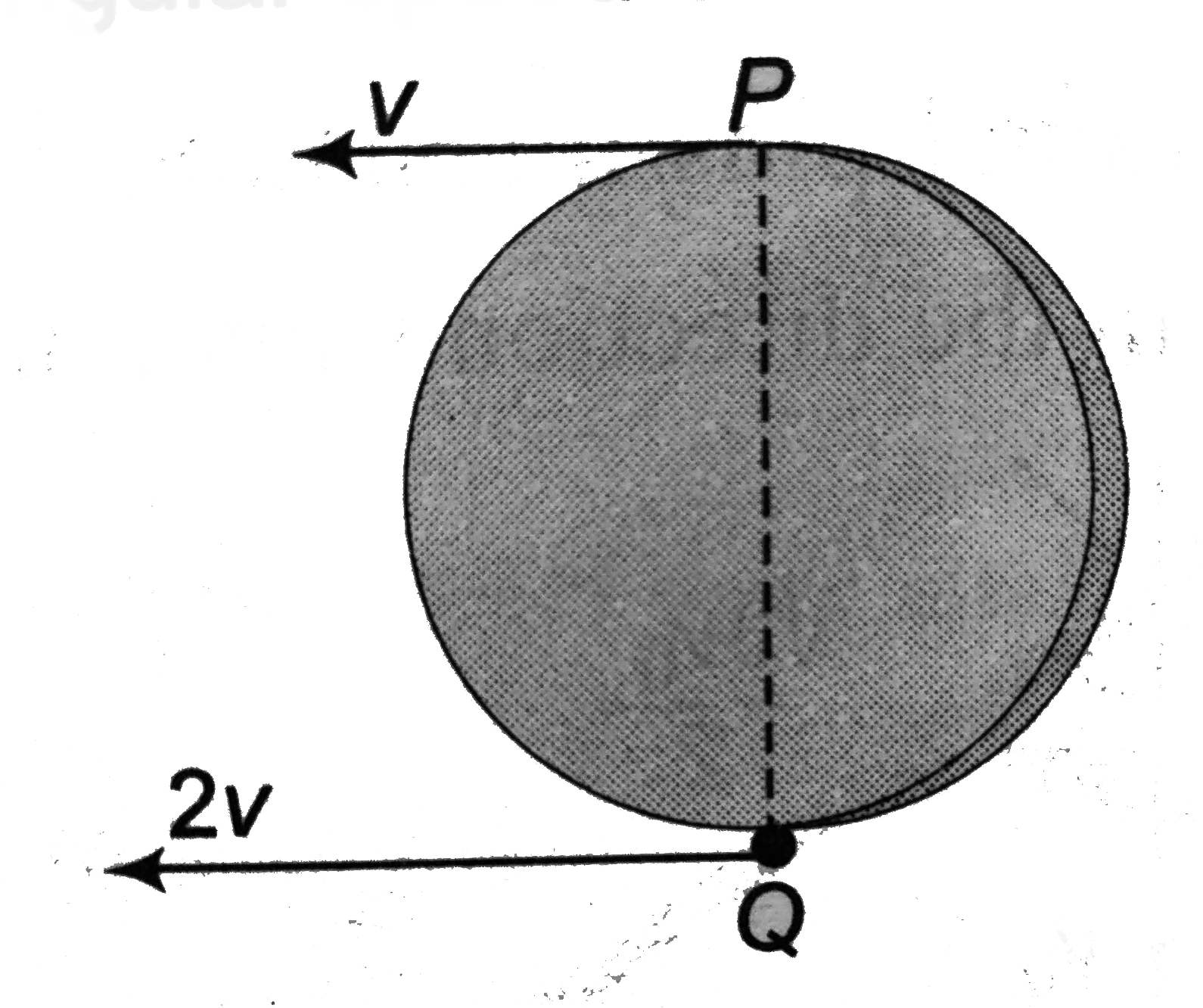
Two point P and Q. diametrically opposite on a disc of radius R have linear velocities v and 2v as shown in figure. Find the angular speed of the disc.View SolutionA disc of radius R is rotating with an angular speed ω0 about a horizontal axis. It is placed on a horizontal table. The coefficient of kinetic friction is μk.
(a) What was the velocity of its centre of mass before being brought in contact with the table ?
(b) What happens to the linear velocity of a point on its rim when placed in contact with the table ?
(c ) What happens to the linear speed of the centre of mass when disc is placed in contact with the table ?
(d) Which force i sresponsible for the effects in (b) and (c ).
(e) What condition should be satisfied for rolling to begin ?
(f) Calculate the time taken for the rolling to begin.View SolutionA uniiform disc of radius r spins with angular velocity ω and angular acceleration α. If the centre of mass of the disc has linear acceleration a, find the magnitude and direction of aceeleration of the point 1,2, and 3.
 View Solution
View Solution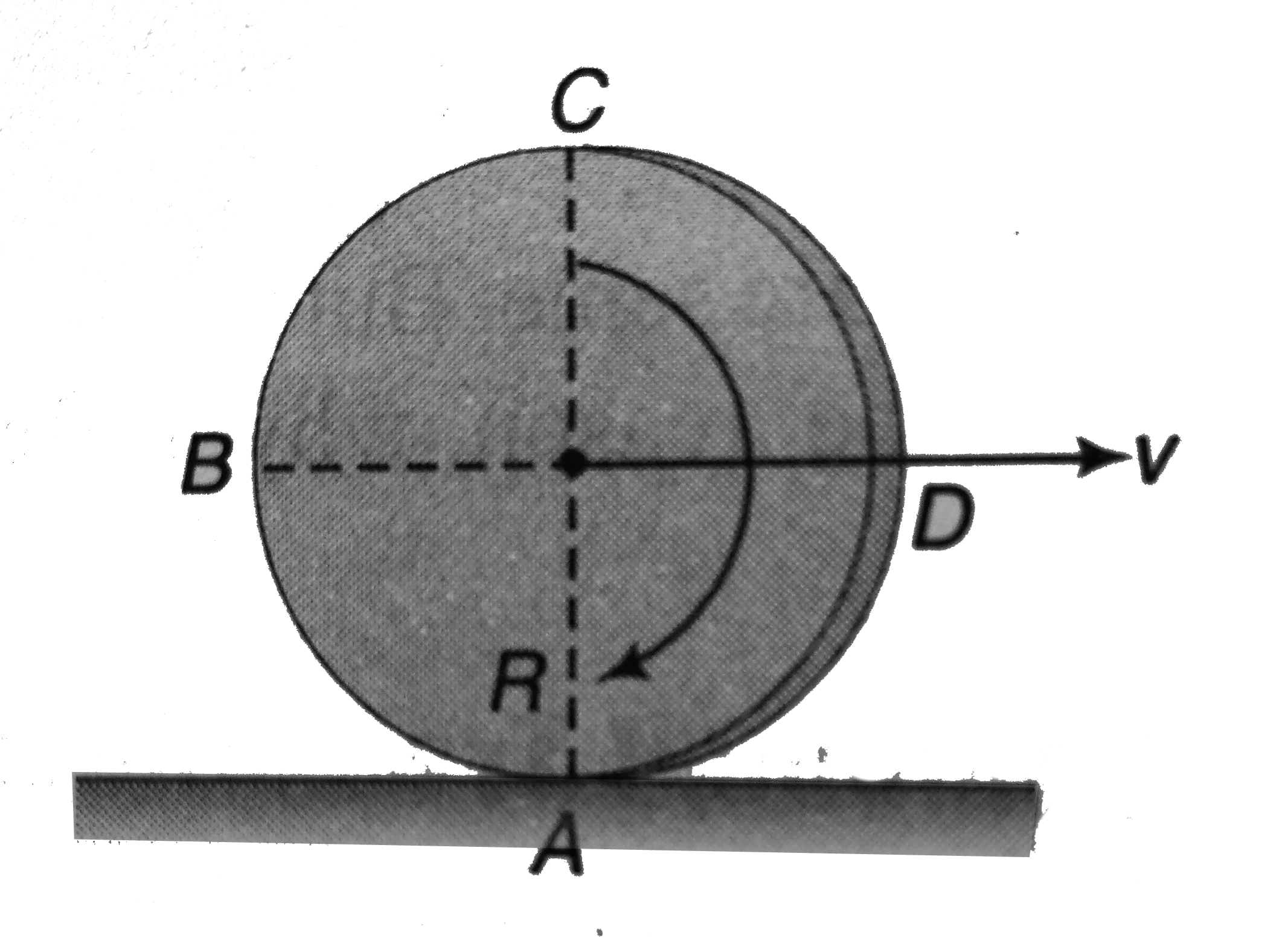
A disc of radius R has linear velocity v and angular velocity ω as shown in the figure. Given υ=rω find velocity of point A, B, C and D on the disc.View SolutionA nonconducing disc of radius R is rotaing about axis passing through its cente and perpendicual its plance with an agular velocity ω . The magnt moment of this disc is .
View Solution

