A door is hinged at one and is free to rotate about a vertical axis [Fig.] Does its weight cause any torque the axis ? Given reason for you answer.
![A door is hinged at one and is free to rotate about a vertical axis [Fig.] Does its weight cause any torque the axis ? Given reason for you answer.](https://d10lpgp6xz60nq.cloudfront.net/physics_images/PR_XI_V01_C05_S01_306_Q01.png)
No. As →τ=→r×→F, therefore torque is produced by a force along a direction normal to the force.
If the door is in xy plane, the torque produced by its weight can only be along ±z direction. It can never be about an axis passing through x-direction of y-direction.
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SHORT ANSWER QUESTIONS II.2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - LONG ANSWER QUESTIONS26videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SHORT ANSWER QUESTIONS I.2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
A bullet of mass 10g and speed 500m/s is fired into a door and gets embedded exactly at the centre of the door. The door is 1.0m wide and weight 12kg. It is hinged at one end and rotates about a vertical axis practically without friction. Find the angular speed of the door just after the bullet embeds into it.(Hint. The moment of inertia of the door about the vertical axis at one end is ML2/3)
View SolutionThe figure shows three small spheres that rotate about a vertical axis. The perpendicular distance between the axis and the center of each sphere is given. Rank the three spheres according to their rotational inertia about that axis, greatest first.
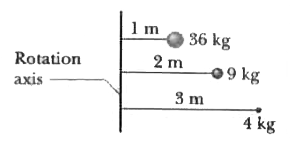
View Solution
Knowledge Check
- Question 1 - Select One
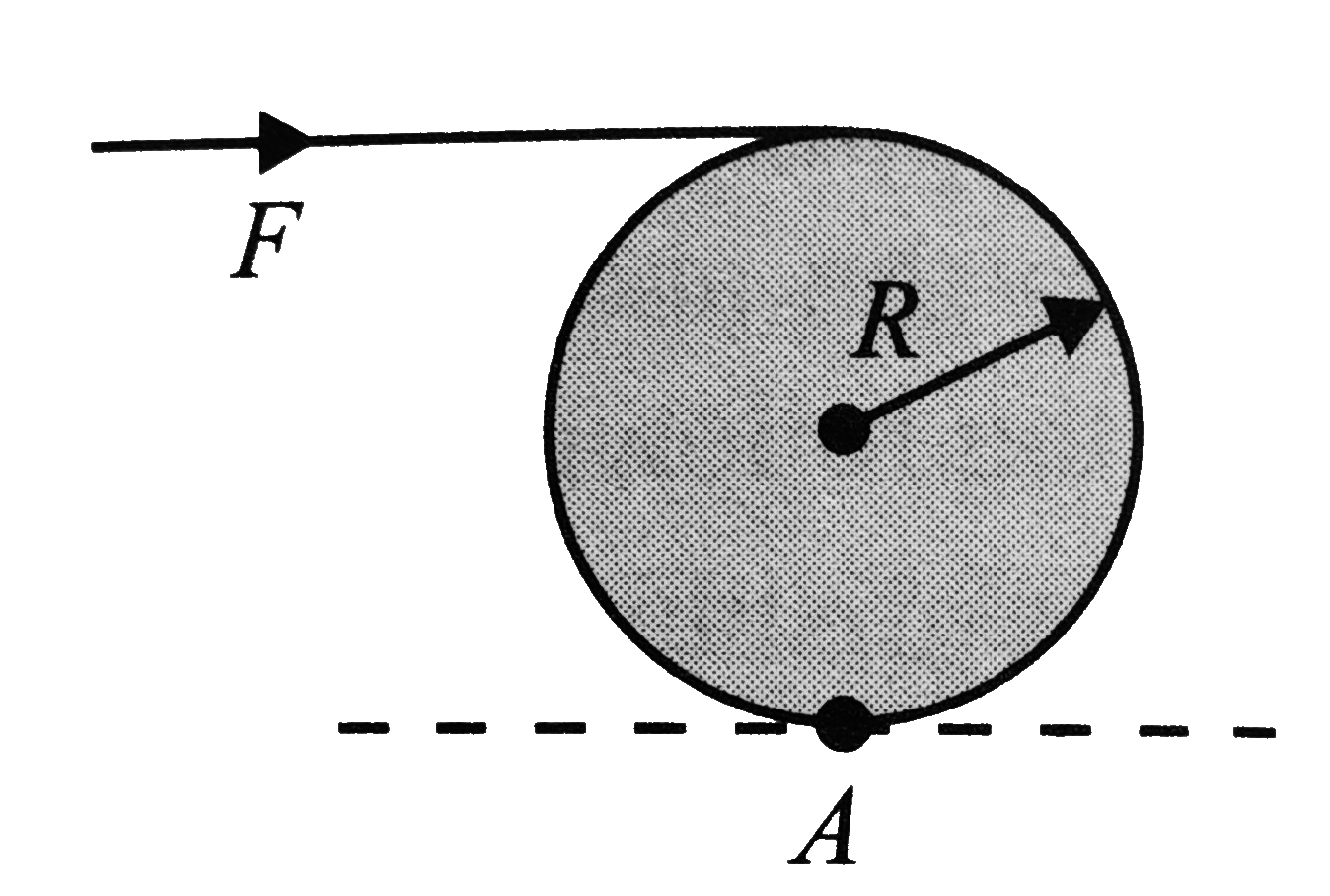
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
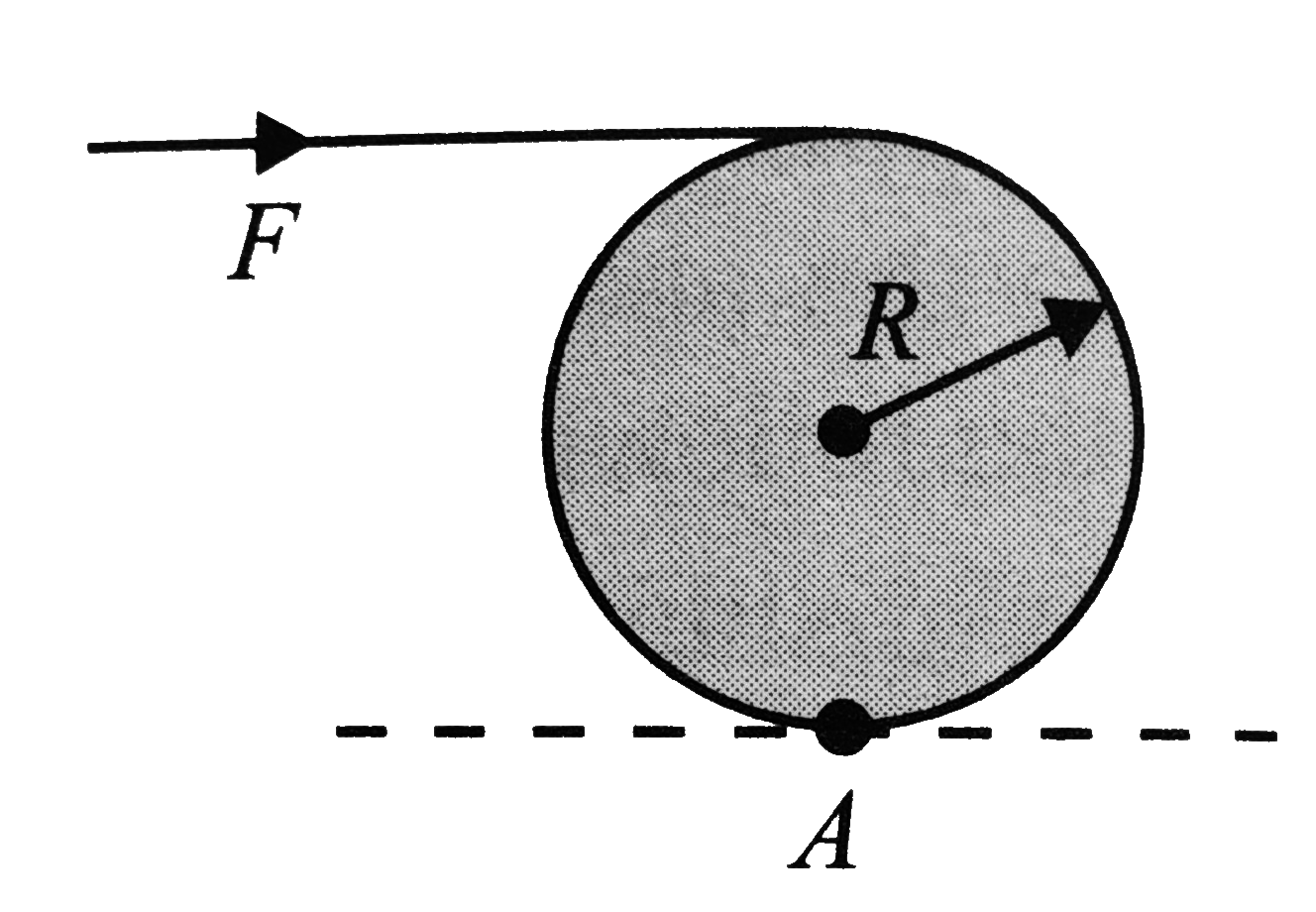
Component of reaction at the hinge in the vertical direction isA43mgBmgCMg2D23mg - Question 2 - Select One
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
Component of reaction at the hinge in the horizontal direction isAF4BFCF3DF2 - Question 3 - Select One
The time taken by earth to complete one rotation about its axis is
A12 hoursB16 hoursC24 hoursD365 days
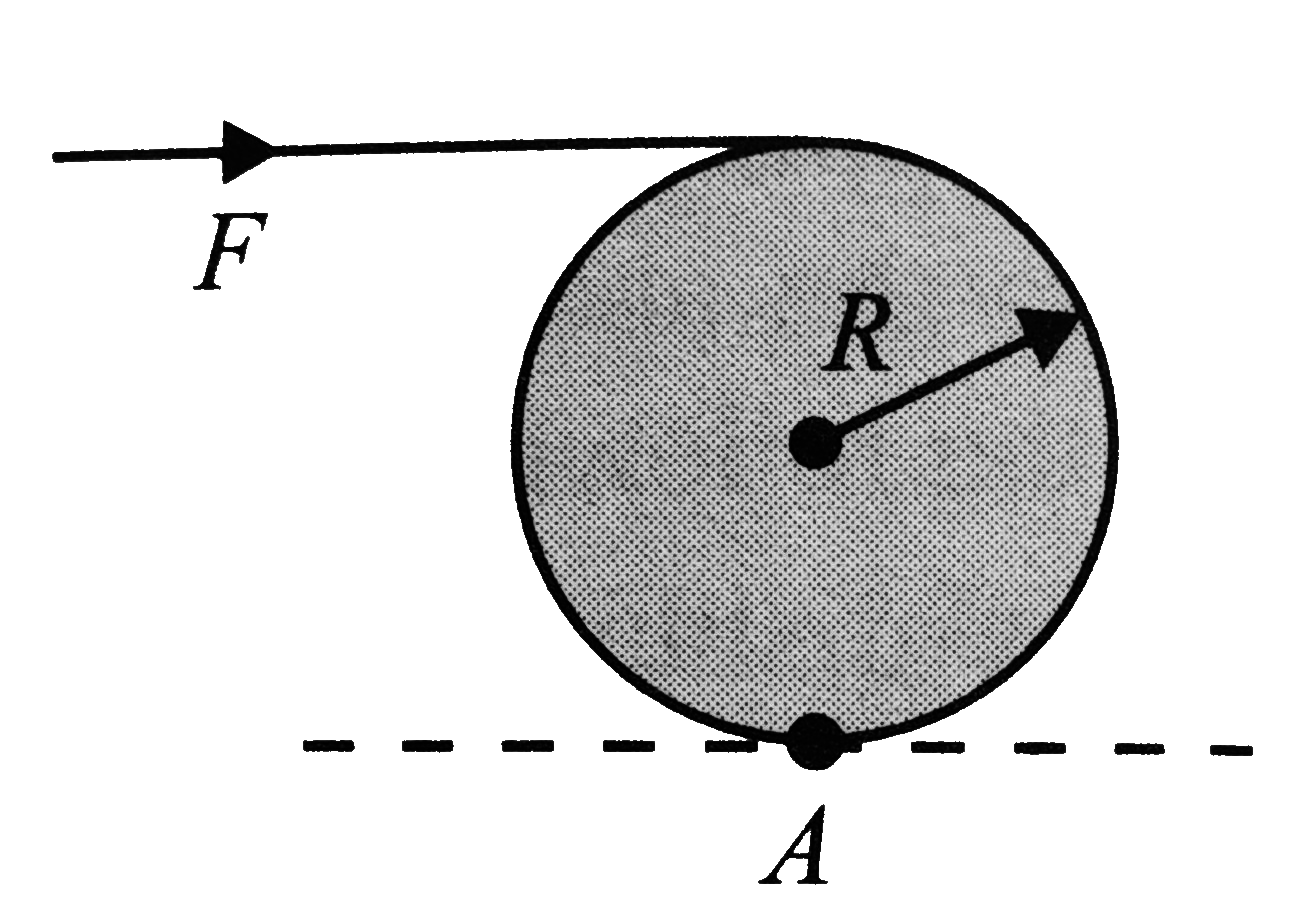
When a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
Tangential acceleration of the centre of mass isView SolutionIf a horizontal cylindrical tube, partly filled with water is rapidly rotated about a vertical axis passing through its centre, the moment of inertia of the water about its axis will
View SolutionHow many degrees does the Earth rotate about its own axis in one hour?
View SolutionHow many degrees does the Earth rotate about its own axis in one hour?
View SolutionGiven below are two statements labelled as Assertion (A) and Reason (R)
Assertion(A): A magnetic needle free to rotate in a vertical plane, orients itself (with its axis) vertical at the poles of the earth.
Reason (R): At the poles of the earth the horizontal component of earth’s magnetic field will be zero.
Select the most appropriate answer from the options given below:View Solution