equal point masses each of mass are placed at the vertices of a angular n-polygon. The vacent vertex has position vector with respect to the centre of the polygon. Find the position vector of centre of mass.
To find the position vector of the center of mass of (n−1) equal point masses each of mass m placed at the vertices of an angular n-polygon, with the vacant vertex having a position vector a with respect to the center of the polygon, we can follow these steps:
1. Understanding the System:
- We have (n−1) point masses, each of mass m, placed at the vertices of a regular n-polygon.
- The n-polygon has n vertices, and one vertex is vacant. The position vector of this vacant vertex is given as a.
2. Total Mass Calculation:
- The total mass of the system with (n−1) masses is:
\(
M = (n - 1)m
\)
3. Position Vector of the Center of Mass:
- The center of mass (COM) of a system of particles can be calculated using the formula:
\(
\vec{r}_{\text{COM}} = \frac{\sum m_i \vec{r}_i}{\sum m_i}
\)
- In our case, we have (n−1) masses at the vertices of the polygon and one additional mass at the vacant vertex.
4. Adding the Vacant Vertex Mass:
- If we consider the vacant vertex and place a mass m there, the total mass becomes:
\(
M_{\text{total}} = (n - 1)m + m = nm
\)
5. Position Vectors:
- Let’s denote the position vector of the center of mass of the (n−1) masses as →x.
- The position vector of the vacant vertex is given as →a.
6. Setting Up the Equation:
- The center of mass of the entire system (including the vacant vertex) can be expressed as:
\(
\vec{0} = \frac{(n - 1)m \vec{x} + m \vec{a}}{nm}
\)
- Simplifying this, we have:
\(
0 = (n - 1) \vec{x} + \vec{a}
\)
7. Solving for \(\vec{x}\):
- Rearranging the equation gives:
\(
(n - 1) \vec{x} = -\vec{a}
\)
- Therefore, the position vector of the center of mass is:
\(
\vec{x} = -\frac{\vec{a}}{n - 1}
\)
Final Result:
The position vector of the center of mass of the (n−1) equal point masses is:
\(
\vec{x} = -\frac{\vec{a}}{n - 1}
\)
- We have (n−1) point masses, each of mass m, placed at the vertices of a regular n-polygon.
- The n-polygon has n vertices, and one vertex is vacant. The position vector of this vacant vertex is given as a.
- The total mass of the system with (n−1) masses is:
\(
M = (n - 1)m
\)
- The center of mass (COM) of a system of particles can be calculated using the formula:
\(
\vec{r}_{\text{COM}} = \frac{\sum m_i \vec{r}_i}{\sum m_i}
\)
- In our case, we have (n−1) masses at the vertices of the polygon and one additional mass at the vacant vertex.
- If we consider the vacant vertex and place a mass m there, the total mass becomes:
\(
M_{\text{total}} = (n - 1)m + m = nm
\)
- Let’s denote the position vector of the center of mass of the (n−1) masses as →x.
- The position vector of the vacant vertex is given as →a.
- The center of mass of the entire system (including the vacant vertex) can be expressed as:
\(
\vec{0} = \frac{(n - 1)m \vec{x} + m \vec{a}}{nm}
\)
- Simplifying this, we have:
\(
0 = (n - 1) \vec{x} + \vec{a}
\)
- Rearranging the equation gives:
\(
(n - 1) \vec{x} = -\vec{a}
\)
- Therefore, the position vector of the center of mass is:
\(
\vec{x} = -\frac{\vec{a}}{n - 1}
\)
The position vector of the center of mass of the (n−1) equal point masses is:
\(
\vec{x} = -\frac{\vec{a}}{n - 1}
\)
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SHORT ANSWER QUESTIONS II.
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:LONG ANSWER QUESTIONS
Explore 26 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:SHORT ANSWER QUESTIONS I.
Explore 2 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Position of the centre of mass is :-
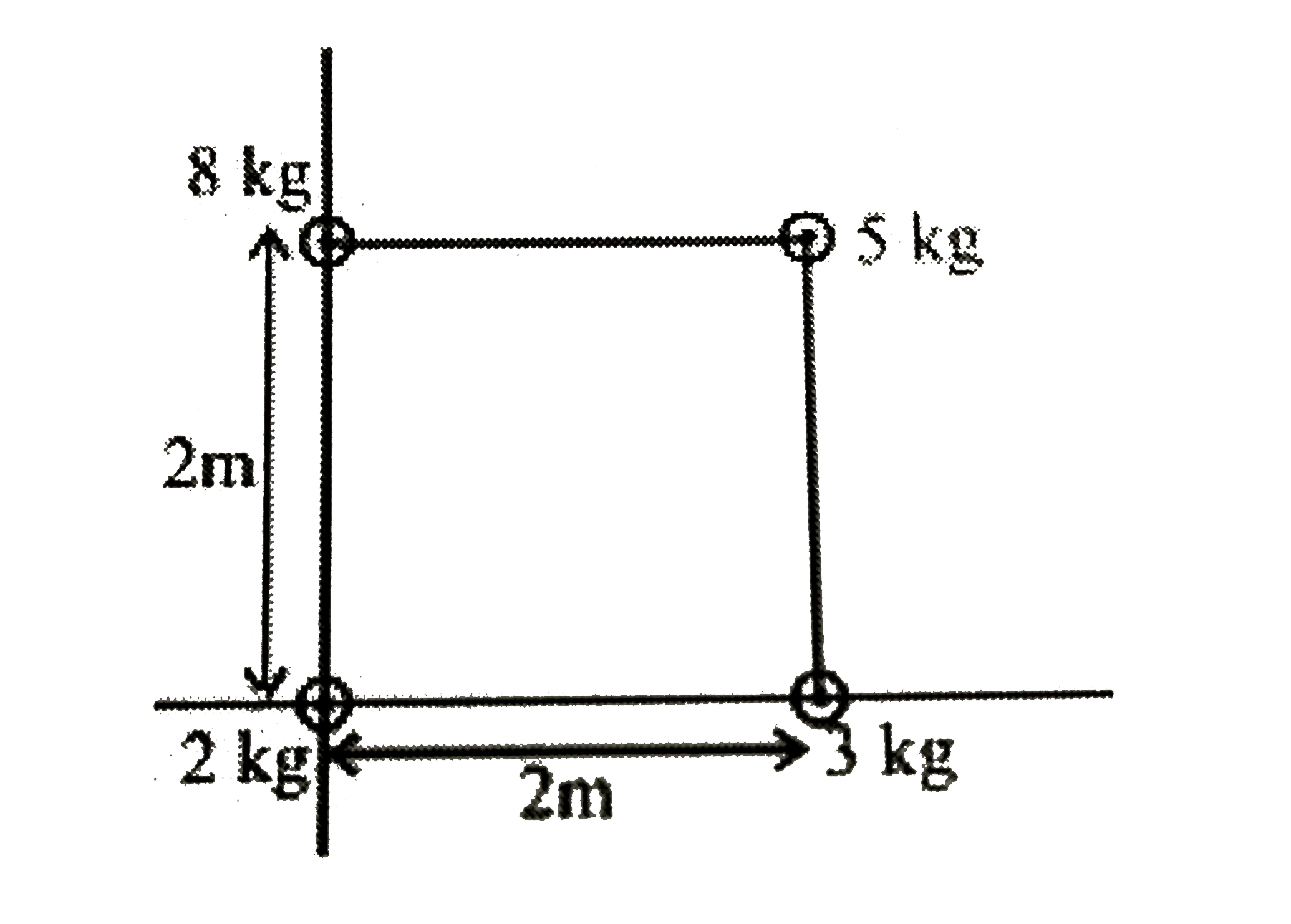
View SolutionThree identical spheres , each of mass M , are placed at the corners of a right angled triangle with mutually perpendicular sides equal to 2 m . Taking their point of intersection as the origin , find the position vector of centre of mass
View Solution
Knowledge Check
Three identical spheres of mass M each are placed at the corners of an equilateral triangle of side 2 m. Taking one of the corners as the origin, the position vector of the centre of mass is
A√3(ˆi−ˆj)Bˆi√3+ˆjCˆi+ˆj/3Dˆi+ˆj/√3Three particles , each of mass m, are placed at the vertices of a right angled triangle as shown in figure. The position vector of the center of mass of the system is (O is the origin and ˆi,ˆj,ˆk are unit vectors)
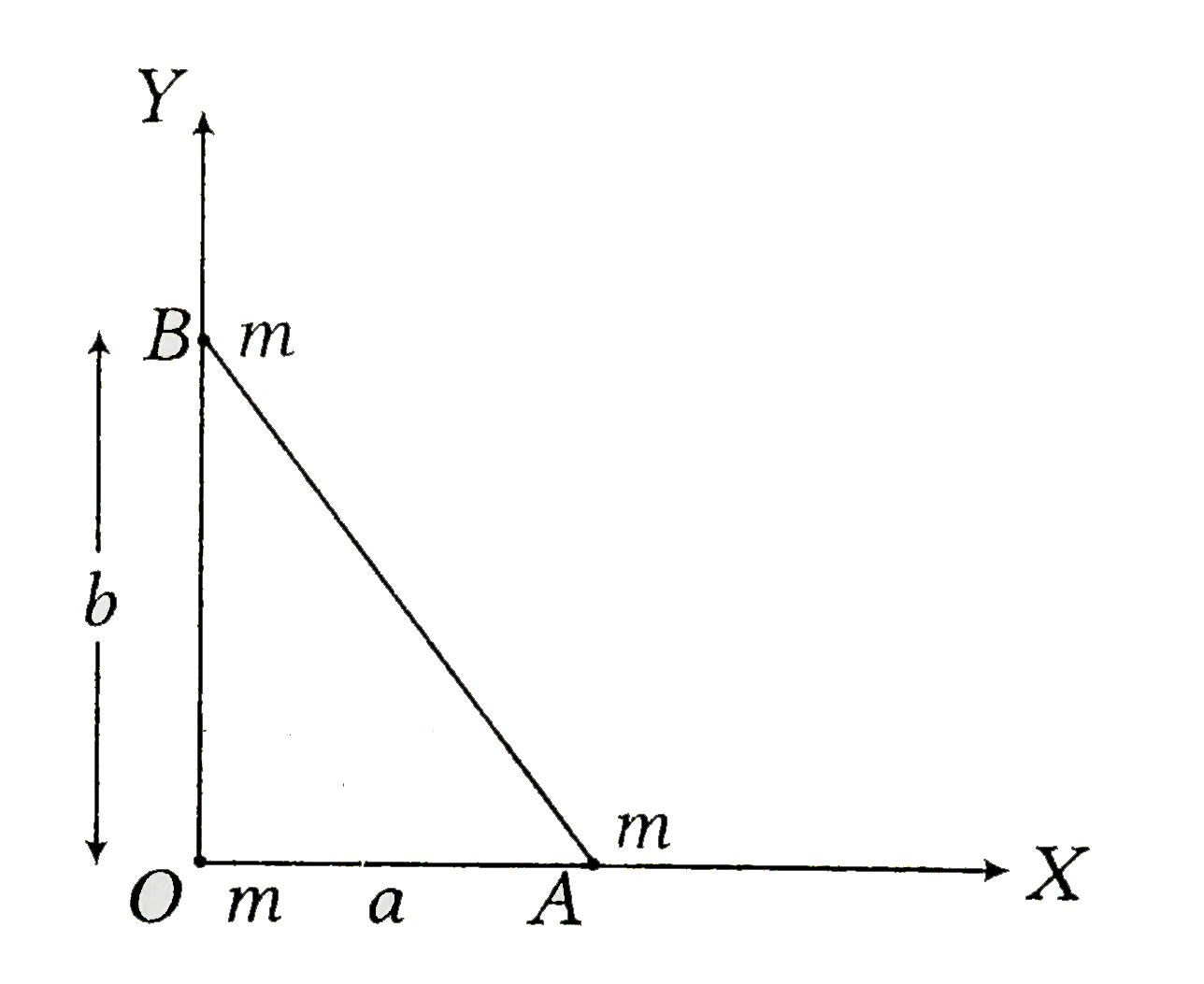 A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)
A13(aˆi−bˆj)B23(aˆi−bˆj)C23(aˆi+bˆj)D13(aˆi+bˆj)Three identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
A√3(I∩−j∩)BI∩√3+j∩CI∩+j∩3DI∩+j∩√3
If a charge q is placed at each vertex of a regular polygon, the net electric field at its centre is zero. Show it.
View Solution(i) A regular polygon has 2016 sides and r is the radius of the circle circumscribing the polygon. Particles of equal mass are placed at 2015 vertices of the polygon. Find the distance of the centre of mass of the particle system from the centre of the polygon.
(ii) In the last problem you have been asked to remove any one particle from the system so that the centre of mass of the remaining 2014 particles lies farthest from the geometrical centre of the polygon. Which particle will you remove ?
View SolutionFind out the position of centre of mass of two particle system.
View SolutionThree identical spheres of mass m each are placed at the corners of an equilateral triangle of side 2m taking one of the corner as the origin the position vector of the centre of mass is
View SolutionThree equal masses each of 50 g, are placed at the corners of a right angled isoceles triangle whose two equal sides are 5 cm each. The position of the centre of mass of the system is
View Solution