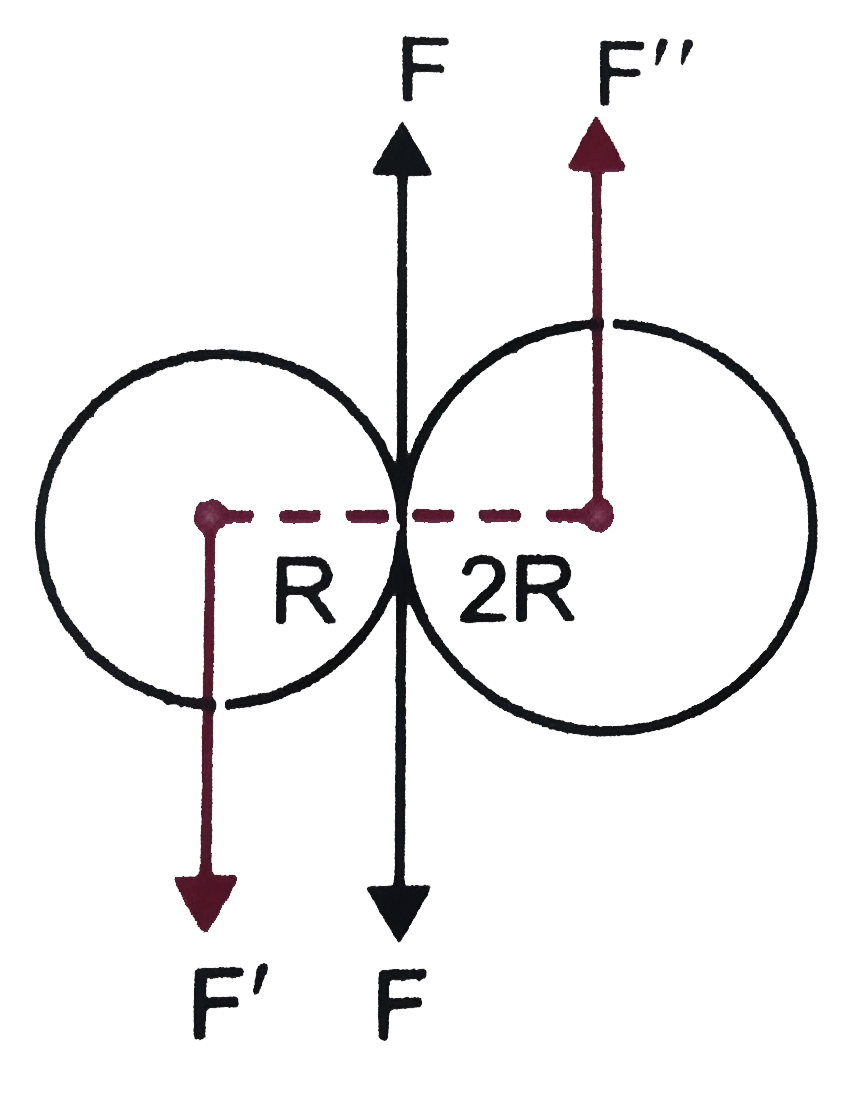
Two cylindrical hollow drums of radii Rand2R, and of a commom height h, are rotating with angular velocities ω (anti-clockwise) and ω (clockwise), respectively. Their axes, fixed are parallel and in a horizontal plane separated by (3R+δ). They are now brought in contact (δ→0).
(a) Show the frictional forces just after contact.
(b) Identify forces and torque external to the system just after contact.
(c ) What would be the ratio of final angular velocities when friction ceases ?
(a) In Fig. we have shown the frictional forces on the two drums just after contact.
(b) If F' and F'' are external forces through support on the left and right drums respectively, then
F'=F=F''
∴Fnet=0.
At distance between the centre of two drums =R+2R=3R, therefore, external torque,
τ=F×3R, anticlockwise.
(c) Let ω1 be final angular velocity of left drum in anticlockwise direction and ω2 be final angular velocity of right drum in clockwise direction. As there will be no friction, finally.
∴R(ω1)=2R(ω2)orω1ω2=21
Topper's Solved these Questions
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE E1videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ADVANCED PROBLEMS FOR COMPETITIONS20videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SHORT ANSWER QUESTIONS II.2videos
SYSTEMS OF PARTICLES AND ROTATIONAL MOTION
- BOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)25videos
RAY OPTICS
- BOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions19videos
THERMODYNAMICS
Similar Questions
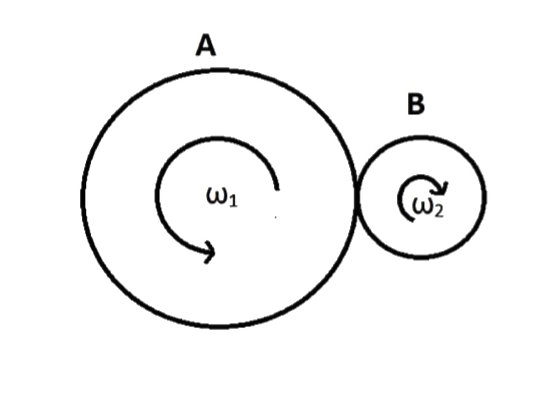
Two discs A and B are in contact and rotating with angular velocity with angular velocities ω1andω2 respectively as shown. If there is no slipping between the discs, then
 View Solution
View SolutionA : Static friction force is a self adjusting force.
R : The interatomic forces at the point of contact give rise to friction between the surfaces.View Solution
Knowledge Check
- Question 1 - Select One
A torque T acts on a body of moment of inertia l rotating with angular speed ω. It will be stopped just after time
AlTωBlωTCTωlDlωT - Question 2 - Select One
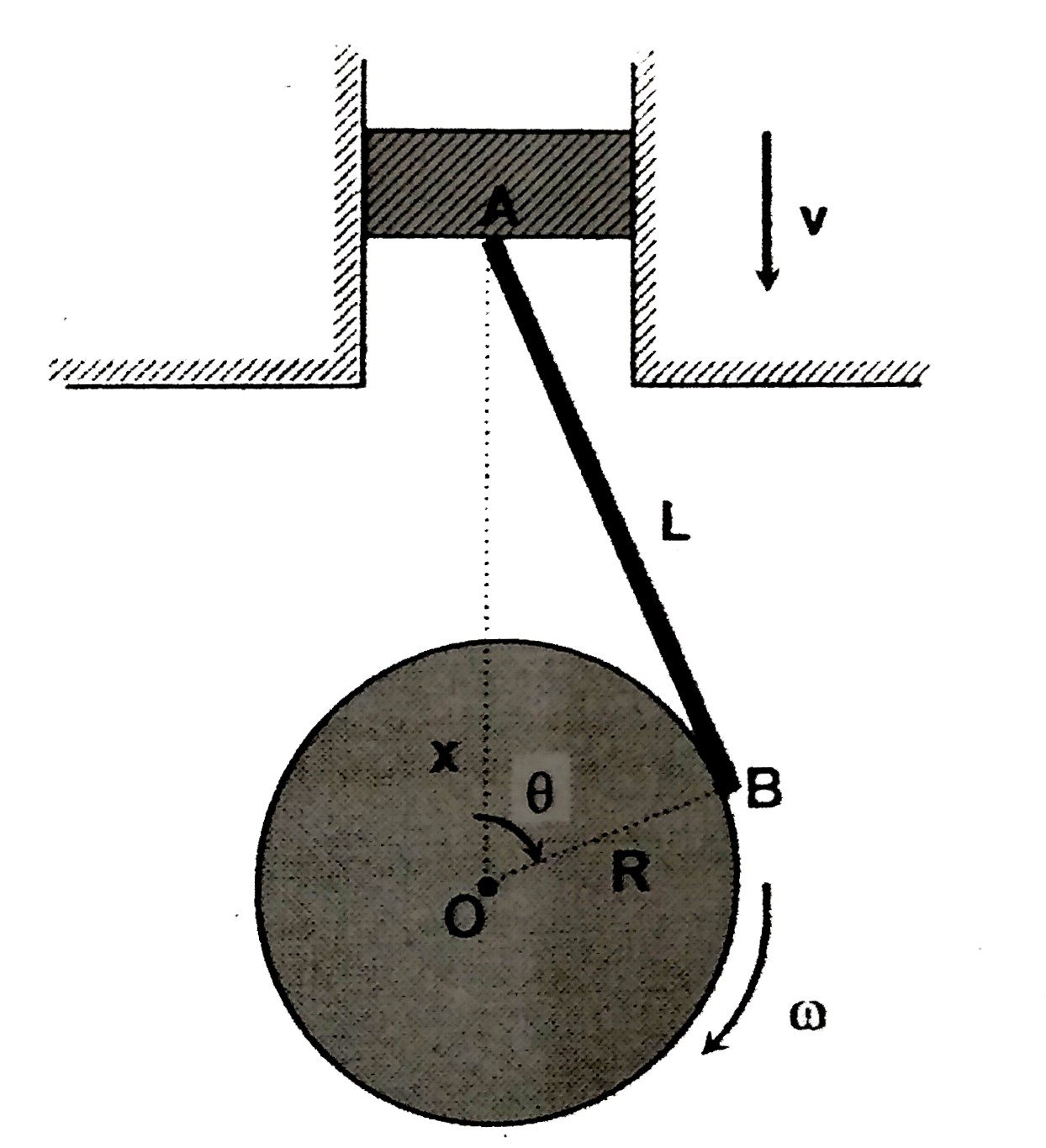
Find velocity of piston A in the given situation if angular velocity of wheel of radius R is ω (constant) in the clockwise sense (O is fixed point)AxRωsinθRcosθ+xBx2ωsinθRcosθ−xCxRωsinθRcosθ−xDR2ωsinθRcosθ−x - Question 3 - Select One
A disc is rotating with angular velocity ω. A force F acts at a point whose position vector with respect to the axis of rotation is r. The power associated with torque due to the force is given by
A(r×F).ωB(r×F)×ωCr×(F.ω)Dr.(F×ω)
A disc of mass M and radius r is rotating with an angular velocity ω. If gently, two masses m each are placed at a distance r/2 on either side of the axis of rotation, what will be the new angular velocity ?
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes, rotating with angular frequencies, ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be A.
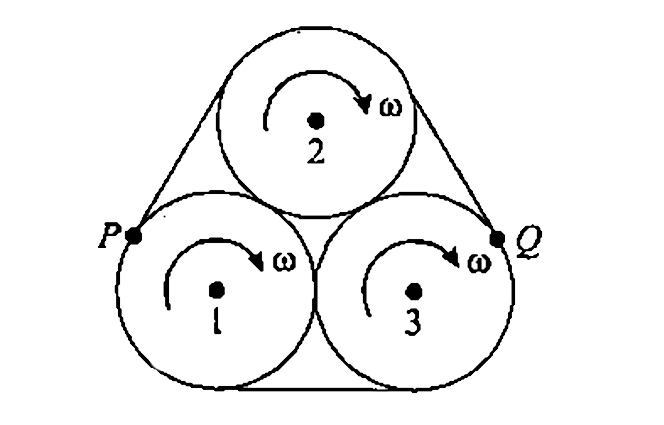
View SolutionThree identical cylinders of radius R are in contact.Each cylinder is rotating with angular velocity ω.A thin belt is moving without sliding on the cylinders. Calculate the magnitude of velocity of point P with respect to Q.P and Q are two points of belt which are in contact with the cylinder.
 View Solution
View SolutionTwo discs of moments of inertia I1 and I2 about their respective axes , rotating with angular frequencies ω1 and ω2 respectively, are brought into contact face to face with their axes of rotation coincident. The angular frequency of the composite disc will be
View SolutionA sphere is moving at some instant with horizontal velocity v0 in right and angular velocity ω in anti clockwise sense. If |v0|=|ωR|, the instantaneous centre of rotation is
View Solution

