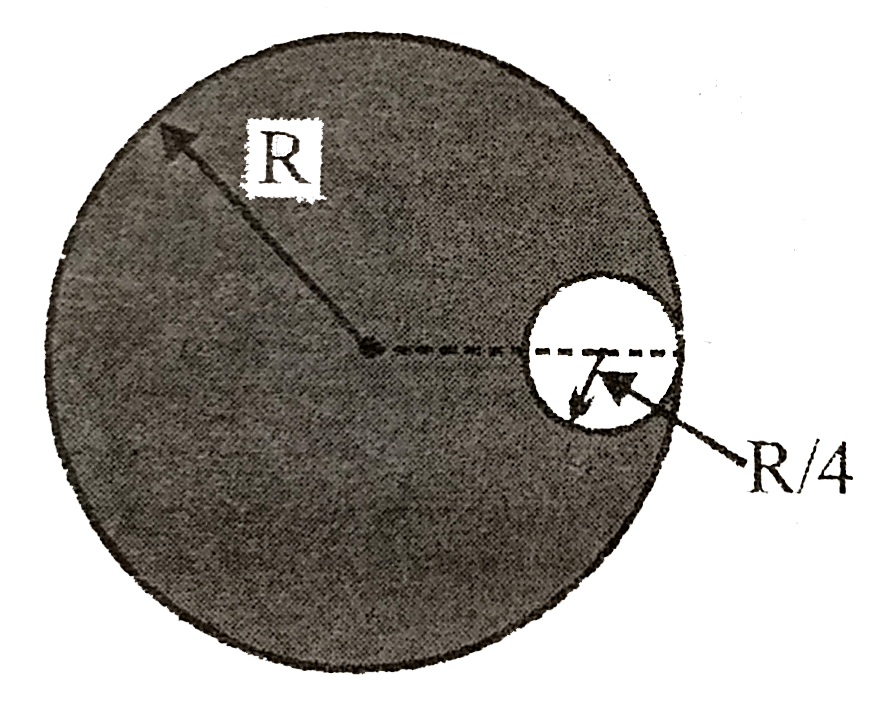
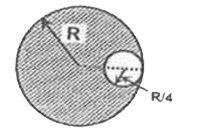
Find the centre of mass of a unifrom (a) half-disc,(b) quarter-disc.
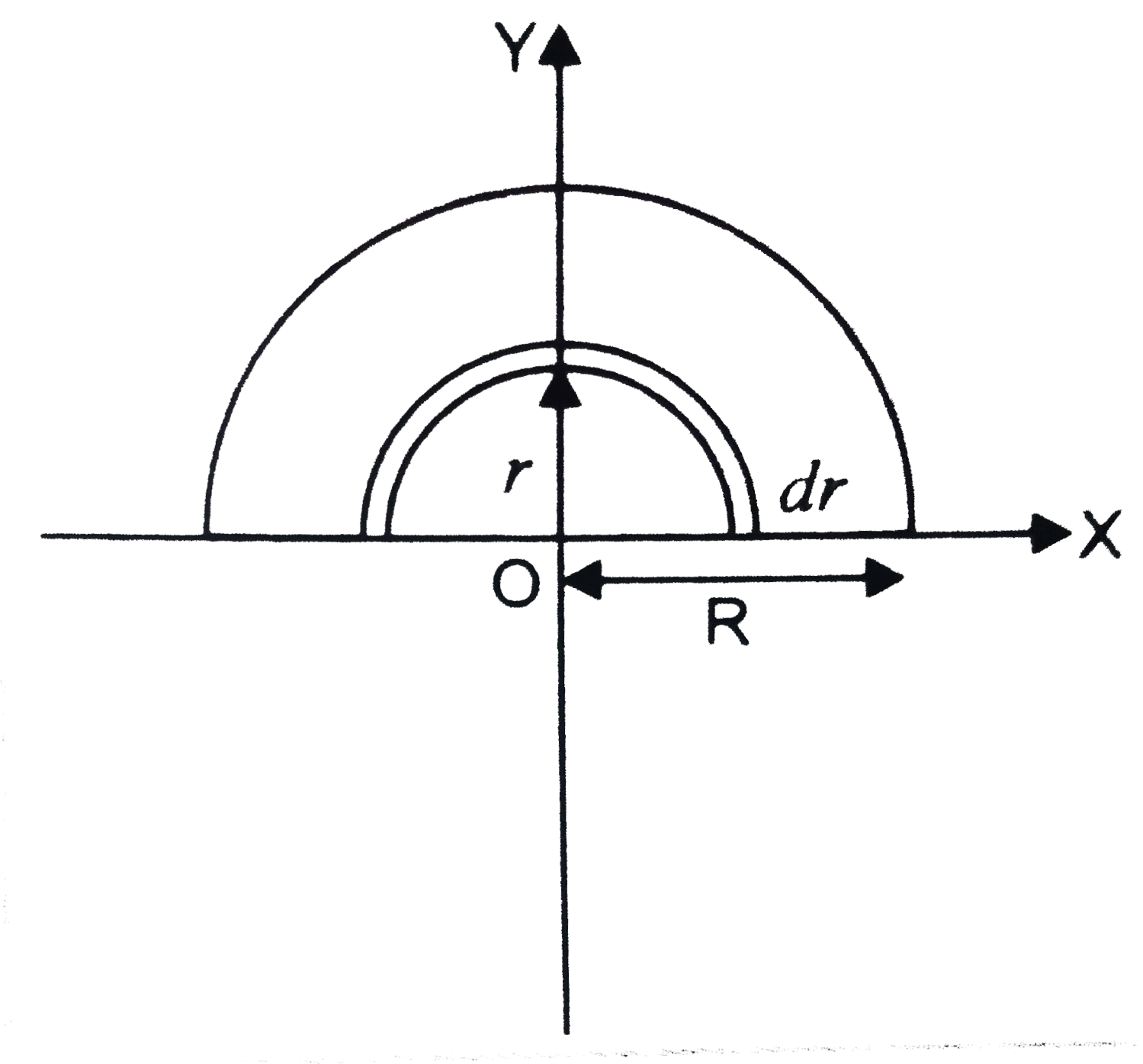
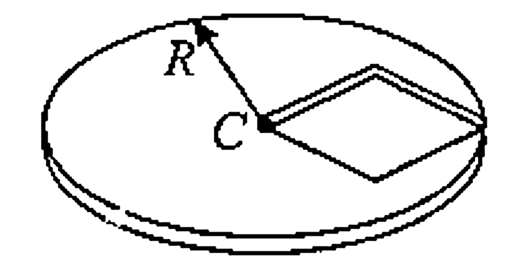
Fig. shown upper half of unifrom circular disc of radius R in XY plane. Let mbe total mass of half disc. Mass per unit area of half
disc =MπR2/2=2MπR2.
The half disc can be supposed to be made up of a large number of semicirular rings, each of mass dm and radii ranging from r=0 to r=R. consider one such semicircular ring of radius r and thickness dr as shown. Surface area of this semicirular ring =(πr)dr.
If (x,y) are co-ordinats of c.m of this element, then (x,y)=(0,2rπ),i.e.,x=0,y=2rπ
Let xcm,ycm be co-ordinates of c.m of semicircular disc.
∴xcm=1M∫R0xdm=1M∫R00dm=0
and ycm=1M∫R0ydm=1M∫R0(2rπ)2MR2rdr=4πR2[r33]R0=4πR2[R33−0]=4R3π
∴c.m of uniform half disc =(0,4R/3π).
(b) Centre of mass of a unifrom quarter disc
Here, mass per unit area of quarter disc =MπR2/4=4MπR2
Proceeding as in (a) above, we can shown that c.m of uniform quarter disc is (4R3π,4R3π)
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SOLVED EXAMPLES TYPE E
1 Video
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - ADVANCED PROBLEMS FOR COMPETITIONS
20 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - SHORT ANSWER QUESTIONS II.
2 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Knowledge Check
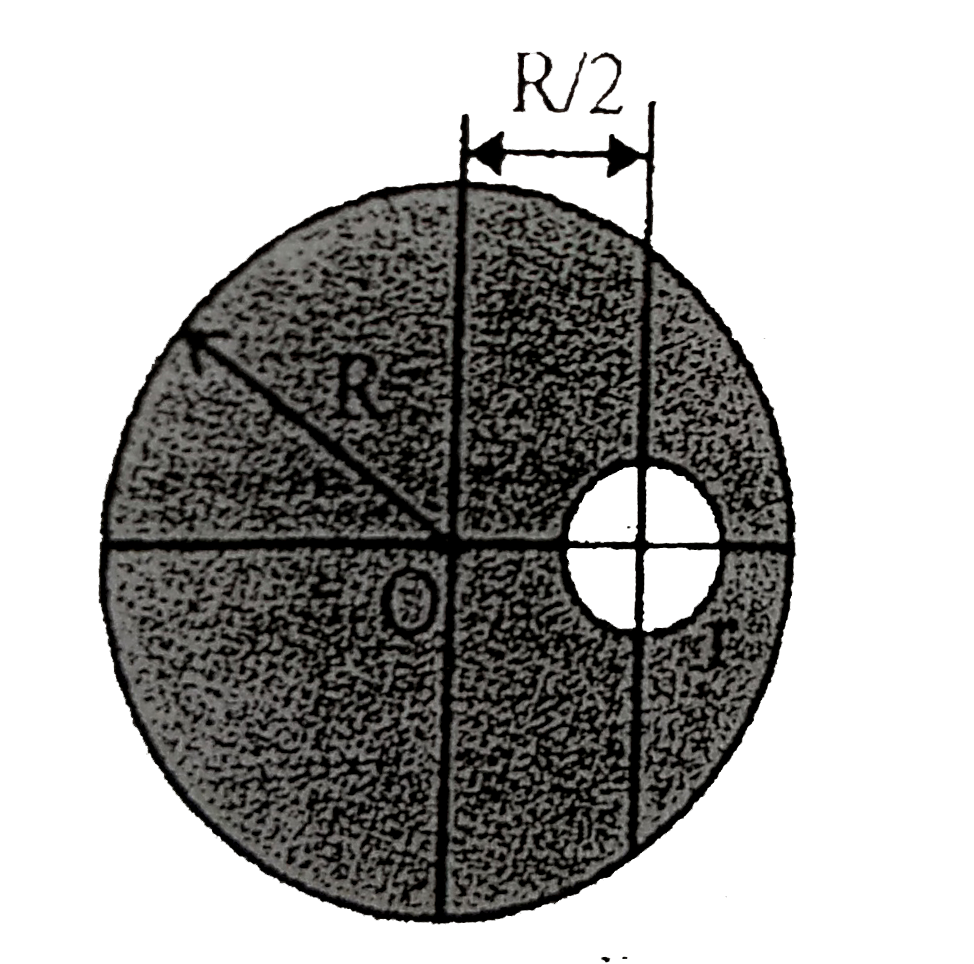
Find the position of centre of mass of a uniform disc of radius R from which a hole of radius is cut out. The centre of the hole is at a distance R/2 from the centre of the disc.
 ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of O
ARr22(R2−r2) towards right of OBRr22(R2−r2) towards left of OC2Rr2(R2+r2) towards right of OD2Rr2(R2+r2) towards left of OA circular hole is cut from a disc of radius 6 cm in such a way that the radius of the hole is 1 cm and the centre of 3 cm from the centre of the disc. The distance of the centre of mass of the remaining part from the centre of the original disc is
A335cmB135cmC310cmDNone of these
Find the centre of mass of the shaded portion of a disc.
View SolutionFind the centre of mass of a thin, uniform disc of radius R from which a small concentric disc of radius r is cut.
View SolutionFind the moment of inertia of a uniform half-disc about an axis perpendicular to the plane and passing through its centre of mass. Mass of this disc is M and radius is R.
View SolutionFind the centre of mass of the disc shown in figure. . A square is removed from the disc as shown
View SolutionFigure-4.11 shows a circular a disc of radius R from which a small disc is cut such that the periphery of the small disc touch the large disc and whose radius is R/2. Find the centre of mass of the remaining part of the disc.

View SolutionFind the centre of mass xCM of the shaded portion of the disc of radius R=24cm.

View Solution