Angular momentum of a particle…………..is……………..of the particle………….. .
Step-by-Step Solution:
1. Understanding Angular Momentum:
- Angular momentum is a vector quantity that represents the rotational motion of a particle about a specific axis. It is denoted by L.
2. Definition of Angular Momentum:
- The angular momentum L of a particle about a given axis is defined as the moment of linear momentum of the particle about that axis.
3. Mathematical Expression:
- The mathematical expression for angular momentum can be given as:
L=r×p
- Here, r is the position vector from the axis of rotation to the point of application of the linear momentum, and p is the linear momentum of the particle.
4. Filling in the Blanks:
- Therefore, we can fill in the blanks in the question:
- Angular momentum of a particle about a given axis is the moment of linear momentum of the particle about that axis.
5. Conclusion:
- This means that the angular momentum quantifies how much rotational motion the particle has around a specific axis, taking into account its linear momentum and the distance from the axis.
Final Answer:
Angular momentum of a particle about a given axis is the moment of linear momentum of the particle about that axis.
---
- Angular momentum is a vector quantity that represents the rotational motion of a particle about a specific axis. It is denoted by L.
- The angular momentum L of a particle about a given axis is defined as the moment of linear momentum of the particle about that axis.
- The mathematical expression for angular momentum can be given as:
L=r×p
- Here, r is the position vector from the axis of rotation to the point of application of the linear momentum, and p is the linear momentum of the particle.
- Therefore, we can fill in the blanks in the question:
- Angular momentum of a particle about a given axis is the moment of linear momentum of the particle about that axis.
- This means that the angular momentum quantifies how much rotational motion the particle has around a specific axis, taking into account its linear momentum and the distance from the axis.
Angular momentum of a particle about a given axis is the moment of linear momentum of the particle about that axis.
Topper's Solved these Questions
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE TYPE A
Explore 2 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:PROBLEMS FOR PRACTICE
Explore 69 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBook:PRADEEPChapter:SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONExercise:MULTIPLE CHOICE QUESTIONS
Explore 151 Videos
- RAY OPTICSBook:PRADEEPChapter:RAY OPTICSExercise:Problem For Practice(a)
Explore 25 Videos
- THERMODYNAMICSBook:PRADEEPChapter:THERMODYNAMICSExercise:Assertion- Reason Type Questions
Explore 19 Videos
Similar Questions
Angular momentum of a particle is the moment of _______ of the particle about the axis rotation.
View SolutionA particle of mass 1kg moves along the curve y=x2 Magnitude of angular momentum of the particle about origin,when particle has x co-ordinate is 12m and x-component of velocity is 4m/s is
View Solution
Knowledge Check
The angular momentum of a particle is
Aparallel to its linear momentumBperpendicular to its linear momentumCinclined to its linear momentumDa scalar quantityA particle of mass m is describing a circular path of radius r with uniform speed. If L is the angular momentum of the particle (about the axis of the circle), then the kinetic energy of the particle is given by
AL2MR2BL24MR2CL22MR2D2L2MR2Angular momentum of the system of particles changes when
Aforce acts on a bodyBtorque acts on a bodyCdirection of velocity changesDnone of these
The z component of the angular momentum of a particle whose position vector is
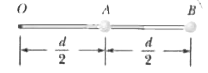
View SolutionFigure 10-74 is an overhead view of a rod of length d and negligible mass that rotates at angular speed ω in the horizontal plane about a vertical axis through point O. Particle A of mass m is attached at the center point and an identical particle B is attached at the far end. Find the angular momentum of particle B with respect to particle A.
View SolutionProve that the angular momentum of a particle is equal to twice the product of its mass and areal velocity.
View SolutionShow that the angular momentum of a particle is equal to twice the product of mass and areal velocity.
View SolutionShow that the angular momentum of a particle is equal to twice the product of mass and areal velocity.
View Solution